Начнем с определителя второго порядка
Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:
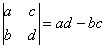
Пример:
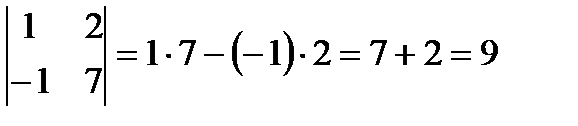
Определителем (или детерминантом) третьего порядка, правило Саррюса.
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":
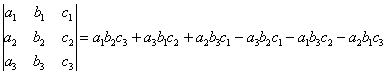
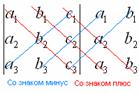
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример:
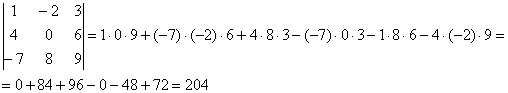
Метод разложения по строке или столбцу:
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
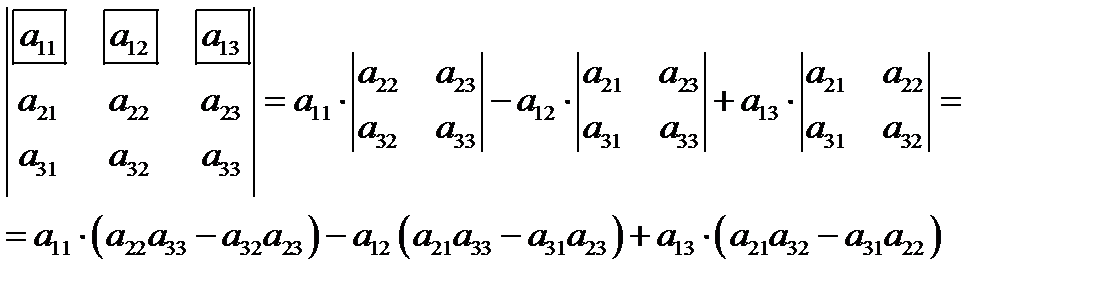
Пример:
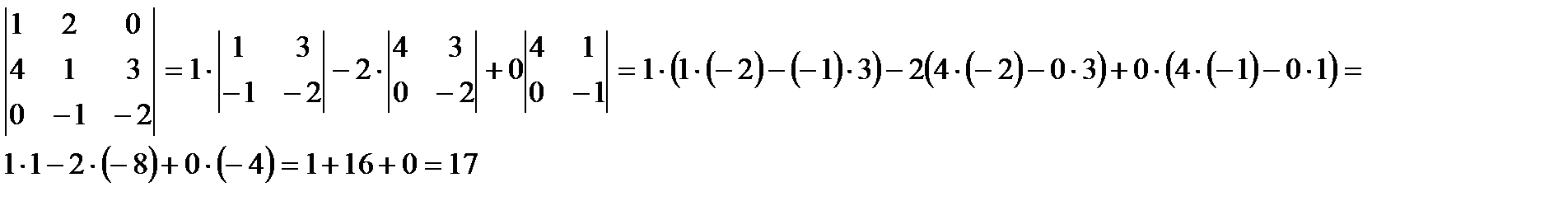
| Тема: | «Решение систем линейных уравнений методом Крамера , методом Гаусса и матричным методом». |
Теоретическая часть:
Системы линейных уравнений
(общие сведения)
Пусть задана система 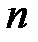 линейных уравнений с
линейных уравнений с 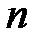 неизвестными
неизвестными
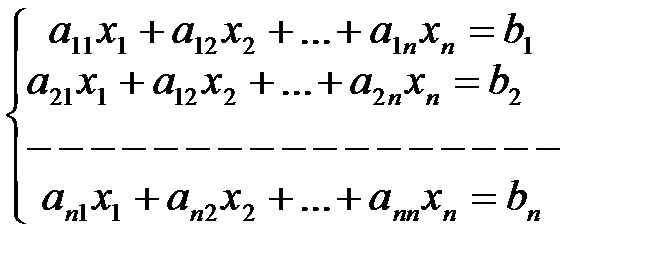 (1)
(1)
|
|
|
Решением системы (1) называется совокупность чисел ( 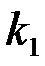 ,
, 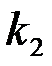 , …,
, …, 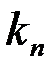 ), которая при подстановке в систему (1) вместо неизвестных обращает каждое уравнение системы в тождество. Система может иметь решение, тогда она называется совместной, причем, если решение единственное, система определенная, если решений множество – система неопределенная. Если система не имеет решений, она называется несовместной. Рассмотрим два способа решения системы: метод Крамера и метод Гаусса.
), которая при подстановке в систему (1) вместо неизвестных обращает каждое уравнение системы в тождество. Система может иметь решение, тогда она называется совместной, причем, если решение единственное, система определенная, если решений множество – система неопределенная. Если система не имеет решений, она называется несовместной. Рассмотрим два способа решения системы: метод Крамера и метод Гаусса.
Метод Крамера
При решении методом Крамера используем определители 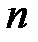 -го порядка. Пусть задана система (1). Составим главный определитель системы из коэффициентов при неизвестных:
-го порядка. Пусть задана система (1). Составим главный определитель системы из коэффициентов при неизвестных:
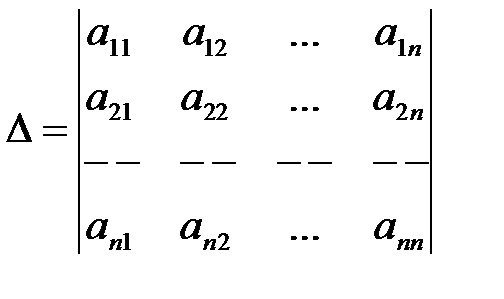 .
.
ТЕОРЕМА. Если определитель системы 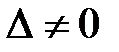 , то систему (3) можно решить по формуле Крамера, причем это решение единственное:
, то систему (3) можно решить по формуле Крамера, причем это решение единственное:
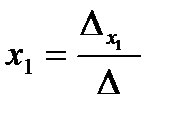 ;
; 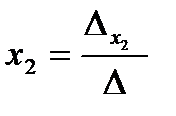 ; … ;
; … ; 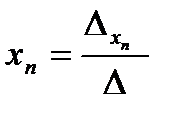 ,
,
где определитель 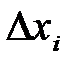 может быть получен из главного определителя путем замены
может быть получен из главного определителя путем замены 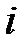 -го столбца на столбец из свободных членов
-го столбца на столбец из свободных членов
Метод Гаусса
Эффективным методом решения и исследования систем линейных уравнений является метод последовательного исключения неизвестных, или метод Гаусса.
|
|
|
Идея метода Гаусса состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, которая легко исследуется и решается.
Пример 2
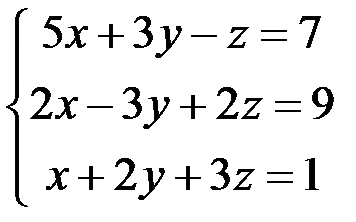 .
.
В результате элементарных преобразований добиваются того, чтобы в последнем уравнении системы осталось одно неизвестное ( 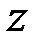 ), во втором – 2 неизвестных (
), во втором – 2 неизвестных ( 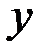 и
и 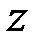 ) а в первом – 3 неизвестных (
) а в первом – 3 неизвестных ( 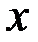 ,
, 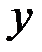 ,
, 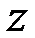 ). За ведущее уравнение берется то, в котором коэффициент при
). За ведущее уравнение берется то, в котором коэффициент при 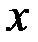 равен 1. Если такого уравнения нет, то его легко получить, разделив любое из уравнений системы на коэффициент при
равен 1. Если такого уравнения нет, то его легко получить, разделив любое из уравнений системы на коэффициент при 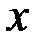 .
.
Ведущим уравнением данной системы будет последнее. Перепишем систему так:
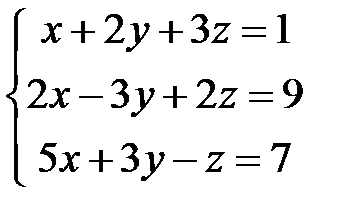 (2)
(2)
Умножаем первое уравнение на (-2) и складываем со вторым, чтобы избавиться от 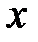 во втором уравнении. Результат сложения записываем на месте второго уравнения. Далее первое уравнение умножаем на (-5) и складываем с третьим, чтобы избавиться от
во втором уравнении. Результат сложения записываем на месте второго уравнения. Далее первое уравнение умножаем на (-5) и складываем с третьим, чтобы избавиться от  в третьем уравнении. Результат записываем на месте третьего уравнения. Первое уравнение при этом переписываем без изменений. Получим:
в третьем уравнении. Результат записываем на месте третьего уравнения. Первое уравнение при этом переписываем без изменений. Получим:
|
|
|
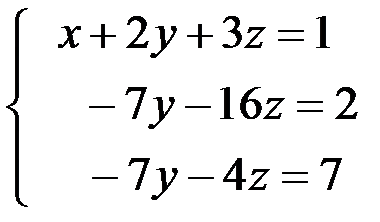 (3)
(3)
Системы уравнений (2) и (3) эквиваленты, т. е. они обе несовместны, или же обе совместны и имеют одни и те же решения.
Умножаем второе уравнение системы (5) на (-1) и складываем с третьим, чтобы избавиться от  в третьем уравнении. Первое уравнение при этом не трогаем. Результат записываем на месте третьего уравнения. Тогда
в третьем уравнении. Первое уравнение при этом не трогаем. Результат записываем на месте третьего уравнения. Тогда
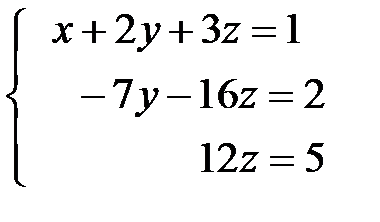 .
.
Из последнего уравнения 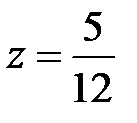 . Подставляем это значение
. Подставляем это значение 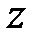 во втрое уравнение системы и находим
во втрое уравнение системы и находим 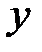 :
:
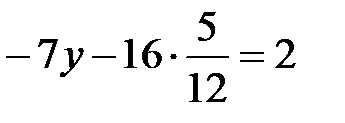
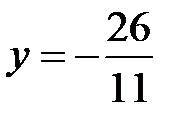 .
.
В первое уравнение подставляем значения 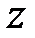 и
и 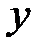 , получаем
, получаем
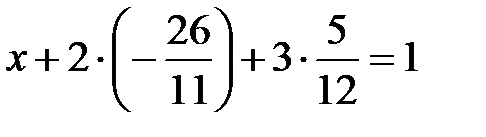
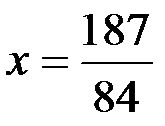 .
.
Ответ: 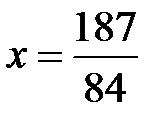 ;
; 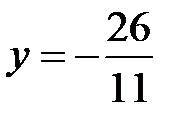 ;
; 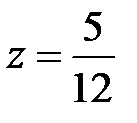 .
.
Рекомендуется сделать проверку.
Матричный способ
Систему можно решить и матричным способом.
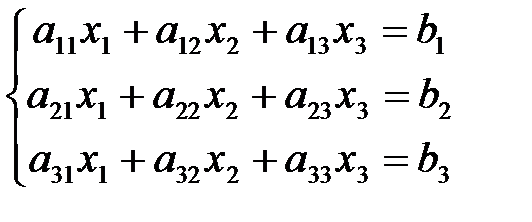
|
|
|
(4)
Составим матрицу системы из коэффициентов при неизвестных:
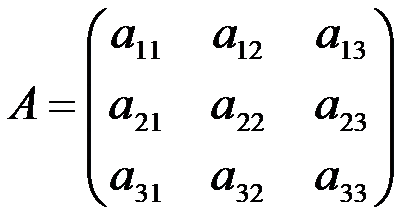 .
.
Из неизвестных 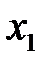 ,
, 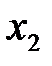 ,
, 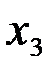 и свободных членов составим матрицы – столбцы
и свободных членов составим матрицы – столбцы
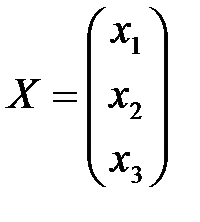 ;
; 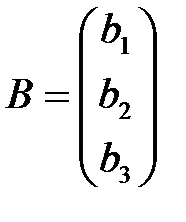 .
.
Тогда система (4) в матричной форме примет вид
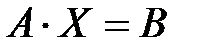 . (5)
. (5)
Чтобы найти матрицу 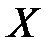 , умножим (7) на
, умножим (7) на 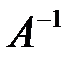 слева.
слева.
A 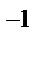
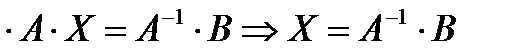
Тема: «Основы теории комплексных чисел. Алгебраическая форма комплексного числа»
В XVI веке итальянский математик Дж.Кордано и Р.Бомбелли, решая квадратное уравнение 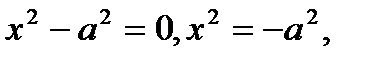 ввели символ
ввели символ 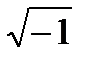 , который в XVIII веке петербургский ученый Л.Эйлер обозначил
, который в XVIII веке петербургский ученый Л.Эйлер обозначил 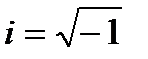 , отсюда решение данного квадратного уравнения имеет вид
, отсюда решение данного квадратного уравнения имеет вид 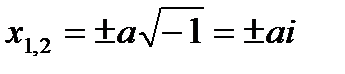 так появилось множество комплексных чисел.
так появилось множество комплексных чисел.
Опр.1.1. Комплексным числом z называется выражение вида 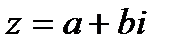 , где a- действительная часть комплексного числа, b-мнимая часть,
, где a- действительная часть комплексного числа, b-мнимая часть, 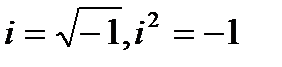 - мнимая единица.
- мнимая единица.
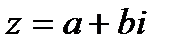 - алгебраическая форма комплексного числа.
- алгебраическая форма комплексного числа.
Опр.1.2. Два к.ч. 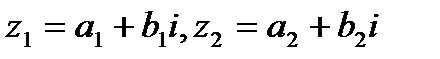 называются равными, если их действительные и мнимые части равны, т.е.
называются равными, если их действительные и мнимые части равны, т.е. 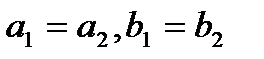 .
.
К.ч. вида 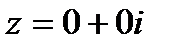 называется нулевым.
называется нулевым.
К.ч. вида 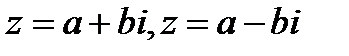 называются комплексно – сопряженными.
называются комплексно – сопряженными.
Пример. 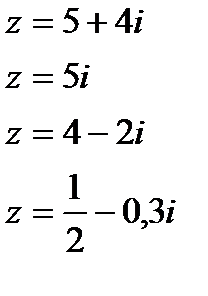
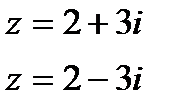 комплексно – сопряженные.
комплексно – сопряженные.
Опр. 1.3. Суммой двух к.ч. 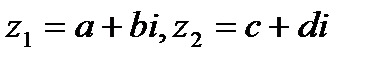 называется к.ч. вида
называется к.ч. вида 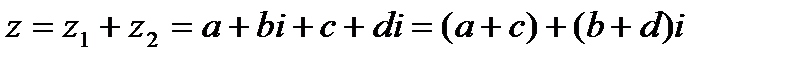 .
.
Опр.1.4. Разностью двух к.ч. 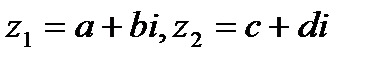 называется к.ч. вида
называется к.ч. вида 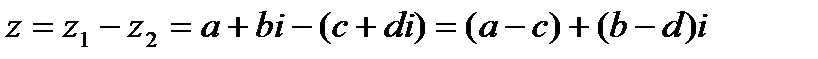 .
.
Пример. 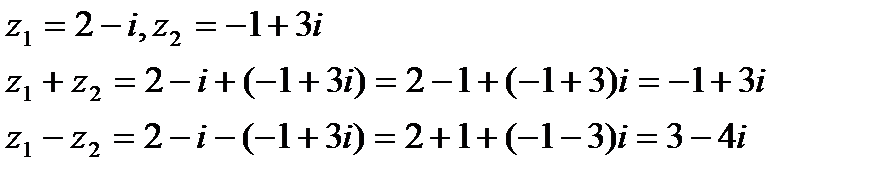
Опр. 1.5. Произведение двух к.ч. 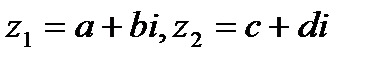 называется к.ч. вида
называется к.ч. вида 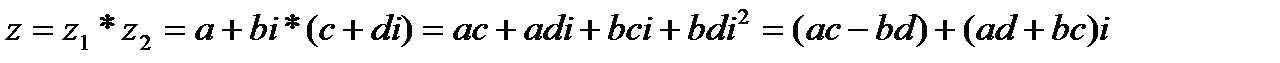 .
.
Пример. 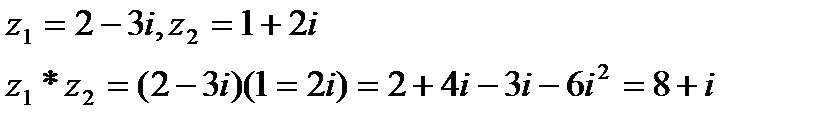
Опр. 1.6. Частным двух к.ч. 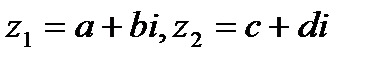 называется к.ч. вида
называется к.ч. вида 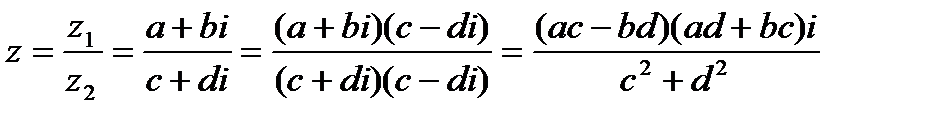
Пример. 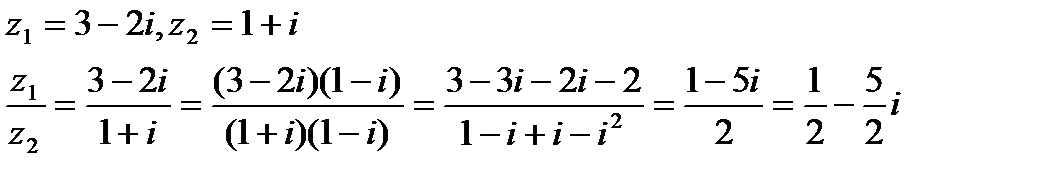
Дата добавления: 2020-01-07; просмотров: 113; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
