Примеры олимпиадных заданий с призмой
Пример 1. В шар, объем которого равен V , вписана прямая треугольная призма. Основанием призмы служит прямоугольный треугольник с острым углом 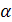 , а наибольшая ее боковая грань есть квадрат. Найти объем призмы.
, а наибольшая ее боковая грань есть квадрат. Найти объем призмы.
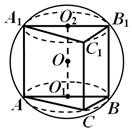
Рис.13
Решение. Сначала определим положение центра шара относительно призмы. Сечения шара плоскостями оснований призмы - круги, в которые вписаны эти основания (рис. 13), а так как основания призмы равны, то равны и одинаково удалены от центра шара круги сечений. Каждый из центров О1 и О2совпадает с серединой соответствующей гипотенузы.
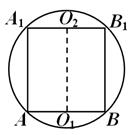
Рис.14
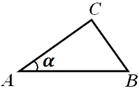
Рис.15
Из свойств сечений шара плоскостью известно, что перпендикуляр, проведенный из центра шара О кплоскости круга сечения, проходит через центр этого круга. Следовательно, О1О 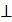 плоскости АВС. Прямая О1О проходит также через O2 и перпендикулярна плоскости
плоскости АВС. Прямая О1О проходит также через O2 и перпендикулярна плоскости 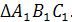 Таким образом, центр шара лежит на грани
Таким образом, центр шара лежит на грани 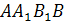 в середине отрезка O1O. Все боковые грани призмы — прямоугольники, причем грань
в середине отрезка O1O. Все боковые грани призмы — прямоугольники, причем грань 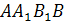 — наибольшая из них (так как АВ — гипотенуза треугольника A ВС). Эта грань по условию — квадрат. Сечение шара плоскостью грани
— наибольшая из них (так как АВ — гипотенуза треугольника A ВС). Эта грань по условию — квадрат. Сечение шара плоскостью грани 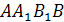 — большой круг шара, поэтому радиус круга, изображенного на рис. 14, равен радиусу шара R . Заметим, что высота призмы АА1= a4 =
— большой круг шара, поэтому радиус круга, изображенного на рис. 14, равен радиусу шара R . Заметим, что высота призмы АА1= a4 = 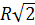 . Теперь остается найти площадь основания:
. Теперь остается найти площадь основания:
S А B С = 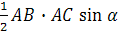 . Из
. Из 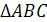 (рис. 15)
(рис. 15)
имеем АС = АВ 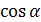 , значит,
, значит,
S А B С = 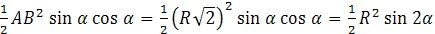 .
.
Теперь получаем:
Vприз. 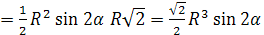 .
.
По условию,
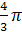 R3 = V,
R3 = V,
|
|
|
откуда R3= 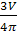 ,следовательно,
,следовательно,
Vприз. 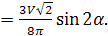
Ответ: Vприз. 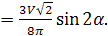
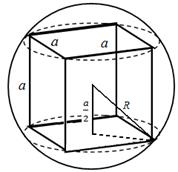
Рис.17
Пример 2. Найти отношение поверхности и объёма шара соответственно к поверхности и объёму вписанного куба
Решение. Пусть радиус шара равен R , ребро куба равно а;
тогда R2 - 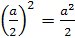 , откуда а=
, откуда а= 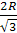 .
.
Обозначим объемы и поверхности шара и куба соответственно через V1, V2, и S1, S2.
Имеем
V1= 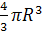 , V2 =
, V2 = 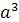 =
= 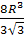 , S1 =4
, S1 =4 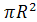 , S2=6а 2 =8R2,
, S2=6а 2 =8R2,
откуда
V1 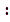 V2 =
V2 = 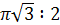 , S1
, S1 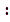 S2 =
S2 = 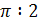 .
.
Ответ: V1 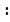 V2 =
V2 = 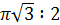 , S1
, S1 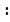 S2 =
S2 = 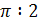 .
.
Примеры олимпиадных заданий с цилиндром
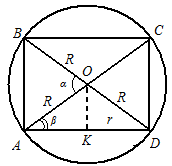
Рис.18
Пример. Найдите отношение объёма шара к объёму прямого кругового цилиндра, вписанного в этот шар, если известно, что меньший угол между диагоналями осевого сечения цилиндра равен 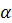 и диаметр основания больше высоты цилиндра (рис. 18).
и диаметр основания больше высоты цилиндра (рис. 18).
Решение. Объём шара нам известен 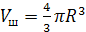 , а объём цилиндра найдём по формуле
, а объём цилиндра найдём по формуле 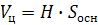 , но
, но 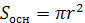 , поэтому
, поэтому 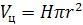
Пусть ABCD - осевое сечение цилиндра (см. рис. 18). Так как диаметр основания, больше высоты цилиндра, то 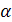 – угол АОВ. Из треугольника АВО следует, что высота цилиндра
– угол АОВ. Из треугольника АВО следует, что высота цилиндра
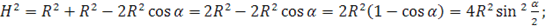
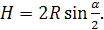
Радиус основания цилиндра
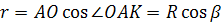 .
.
Угол 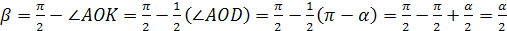 .
.
Получается, что
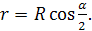
Подставим найденные данные в формулу объёма цилиндра:
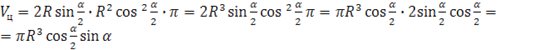 ;
;
Таким образом,
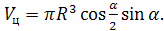
Найдём отношение
|
|
|
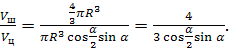
Ответ: 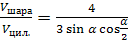 .
.
Примеры олимпиадных заданий с конусом
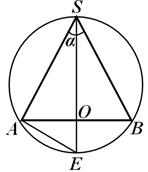
Рис.19
Пример 1. В шар радиуса R вписан круговой конус; угол между образующими конуса в осевом сечении равен α. Найти высоту, образующую и радиус основания конуса.
Решение. Сечение шара, проходящее через ось конуса,— это большой круг шара, в который вписан  АВ S (рис. 19), где A В — диаметр основания конуса. Продолжим высоту (ось) конуса SO до пересечения с окружностью большого круга в точке Е и рассмотрим
АВ S (рис. 19), где A В — диаметр основания конуса. Продолжим высоту (ось) конуса SO до пересечения с окружностью большого круга в точке Е и рассмотрим 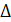 Е S А:
Е S А:
в этом треугольнике
SE = 2R, 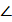 S АЕ = 90° и
S АЕ = 90° и 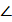 А S Е=
А S Е=  .
.
Поэтому
А S = 2R 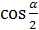 .
.
Теперь из 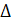 А OS находим
А OS находим
A О= r = 2R 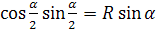 , SO = h=2R
, SO = h=2R 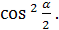
Ответ : SO=2R 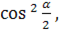 А S = 2R
А S = 2R 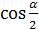 , A О=
, A О= 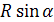 .
.
Пример 2. Отношению высоты конуса к радиусуописанного вокруг него шара равно k . Найти отношение объёмов этих тел. Выяснить при каких k задача имеет смысл.
Рис.20
Решение. Рассмотрим осевое сечение конуса (рис. 20). Пусть h — высота конуса, R — радиус шара, описанного около конуса. Тогда, по условию,  =k, т. е. h = kR .
=k, т. е. h = kR .
Выразим радиус r основания конуса через R; рассмотрев хорды АС и ВЕ, получим:
В D  D Е = А D
D Е = А D  D С (т. к. AD=DC,
D С (т. к. AD=DC,
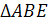 – прямоугольный, AD – высота, опущенного из вершины прямого угла).
– прямоугольный, AD – высота, опущенного из вершины прямого угла).
T. е. 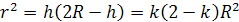
(следовательно, k < 2).
Vш = 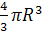 ; Vк =
; Vк = 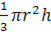 =
= 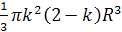 .
.
Таким образом,
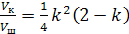 , (при 0 < k < 2).
, (при 0 < k < 2).
|
|
|
Ответ: 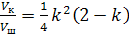 , (при 0 < k < 2).
, (при 0 < k < 2).
Пример 3. В усеченном конусе радиусы нижнего и верхнего оснований равны соответственно r 1 и r 2 , а образующая конуса наклонена к плоскости нижнего основания под углом α (рис. 21). Найти радиус шара, в который вписан данный усеченный конус.
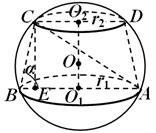
Рис.21
Решение. В сечении шара, проходящем через ось усеченного конуса, получается большой круг шара, в который вписана трапеция АВС D. Рассмотрим 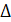 A ВС, который также вписан в большой круг шара. В этом треугольнике известен угол
A ВС, который также вписан в большой круг шара. В этом треугольнике известен угол 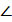 С BA = α. В силу теоремы синусов, АС = 2R
С BA = α. В силу теоремы синусов, АС = 2R 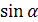 . Таким образом, для определения R достаточно найти АС. Опустим из точки С перпендикуляр СЕ на АВ. Очевидно,
. Таким образом, для определения R достаточно найти АС. Опустим из точки С перпендикуляр СЕ на АВ. Очевидно,
АЕ= r1 + r2, ВЕ = r1 - r2,а СЕ = ( r1 - r2) 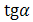 .
.
Поэтому по теореме Пифагора
АС = 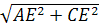 =
= 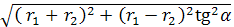 =
=
= 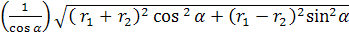 =
= 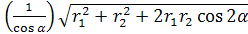 , откуда R =
, откуда R = 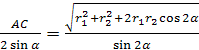 .
.
Ответ: R 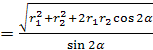 .
.
Примеры заданий ЕГЭ
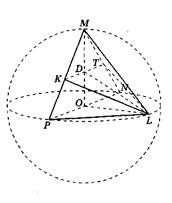
Рис. 22
Дата добавления: 2020-01-07; просмотров: 110; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
