Применение производной при исследовании функций
Максимум и минимум функции
Определение. Функция 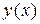 в точке
в точке 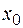 имеет максимум, если значение функции в точке
имеет максимум, если значение функции в точке 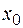 больше, чем ее значение во всех точках некоторого интервала, содержащего точку
больше, чем ее значение во всех точках некоторого интервала, содержащего точку 
Определение. Функция 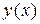 в точке
в точке 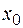 имеет минимум, если значение функции в точке
имеет минимум, если значение функции в точке 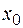 меньше, чем ее значение во всех точках некоторого интервала, содержащего точку
меньше, чем ее значение во всех точках некоторого интервала, содержащего точку 
Функция, определенная на отрезке, может достигать максимума и минимума только для значений аргумента х, принадлежащих данному отрезку.
Максимум и минимум функции называется экстремумами функции.
Теорема (необходимое условие существования экстремума). Если функция 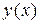 имеет в точке
имеет в точке  экстремум, то ее производная в данной точке
экстремум, то ее производная в данной точке 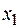 либо обращается в нуль, либо не существует.
либо обращается в нуль, либо не существует.
Теорема (достаточное условие существования экстремума). Пусть функция 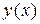 непрерывна в некотором интервале, содержащем критическую точку
непрерывна в некотором интервале, содержащем критическую точку 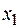 , и дифференцируема во всех точках этого интервала, кроме, быть может, самой точки
, и дифференцируема во всех точках этого интервала, кроме, быть может, самой точки  . Если при переходе через эту точку
. Если при переходе через эту точку  слева направо производная меняет знак с плюса на минус, то в точке
слева направо производная меняет знак с плюса на минус, то в точке  функция имеет максимум. Если же производная меняет знак с минуса на плюс, то функция в точке
функция имеет максимум. Если же производная меняет знак с минуса на плюс, то функция в точке  имеет минимум.
имеет минимум.
Теорема (достаточное условие существования экстремума). Пусть функция 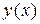 имеет первую производную, обращающуюся в нуль в данной точке
имеет первую производную, обращающуюся в нуль в данной точке  :
:  . Пусть также существует, непрерывна и отлична от нуля в некоторой окрестности и самой точке
. Пусть также существует, непрерывна и отлична от нуля в некоторой окрестности и самой точке  вторая производная
вторая производная  Тогда в точке
Тогда в точке  функция
функция 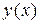 имеет максимум, если
имеет максимум, если  и минимум, если
и минимум, если 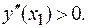
|
|
|
Значения аргумента функции 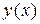 , при которых производная обращается в нуль или не существует, называются критическими точками.
, при которых производная обращается в нуль или не существует, называются критическими точками.
Алгоритм нахождения наибольшего
и наименьшего значения функции на отрезке
1. Определяем критические точки, принадлежащие данному отрезку.
2. Вычисляем значения функции в полученных критических точках.
3. Вычисляем значения функции на концах рассматриваемого отрезка.
4. Из полученных выше значений функции выбираем наибольшее и наименьшее значения.
Пример. Для функции  определить наибольшее и наименьшее значения на отрезке
определить наибольшее и наименьшее значения на отрезке  .
.
Решение. Определяем критические точки данной функции. Для этого находим первую производную и приравниваем ее к нулю:

Оба этих значения принадлежат отрезку  . Находим вторую производную:
. Находим вторую производную:  Так как
Так как  , то в точке
, то в точке  функция имеет минимум,
функция имеет минимум,  Так как
Так как  , то в точке
, то в точке 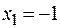 функция имеет максимум,
функция имеет максимум,  Вычисляем значения функции на концах данного отрезка:
Вычисляем значения функции на концах данного отрезка: 
 Таким образом, наибольшее значение данной функции на отрезке
Таким образом, наибольшее значение данной функции на отрезке  есть
есть  а наименьшее
а наименьшее 
Направление выпуклости. Точки перегиба
Определение. График дифференцируемой функции  называется выпуклым вниз на интервале
называется выпуклым вниз на интервале 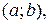 если дуга кривой на этом промежутке расположена выше касательной, проведенной к графику функции
если дуга кривой на этом промежутке расположена выше касательной, проведенной к графику функции  в любой точке
в любой точке  . Если же на интервале
. Если же на интервале  всякая касательная располагается выше дуги кривой, то график дифференцируемой функции на этом интервале называется выпуклым вверх. На рис. 1 график функции
всякая касательная располагается выше дуги кривой, то график дифференцируемой функции на этом интервале называется выпуклым вверх. На рис. 1 график функции  является выпуклым вниз на интервале
является выпуклым вниз на интервале  и выпуклым вверх на интервале
и выпуклым вверх на интервале  .
.
|
|
|
Если функция  дважды дифференцируема на
дважды дифференцируема на  и
и  (
(  ), то ее график является выпуклым вниз (вверх) на этом интервале. В простейших случаях область определения функции
), то ее график является выпуклым вниз (вверх) на этом интервале. В простейших случаях область определения функции  можно разбить на конечное число интервалов с постоянным направлением выпуклости. Каждый из этих интервалов ограничен точками, в которых вторая производная либо равна нулю, либо не существует. Точка
можно разбить на конечное число интервалов с постоянным направлением выпуклости. Каждый из этих интервалов ограничен точками, в которых вторая производная либо равна нулю, либо не существует. Точка  в которой направление выпуклости графика функции меняется на противоположное, называется точкой перегиба.
в которой направление выпуклости графика функции меняется на противоположное, называется точкой перегиба.

Рис. 1.
Теорема (достаточное условие точки перегиба). Пусть функция  дважды дифференцируема в некотором интервале, содержащем точку
дважды дифференцируема в некотором интервале, содержащем точку 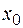 , в которой
, в которой  или
или  не существует. Если при переходе через эту точку вторая производная
не существует. Если при переходе через эту точку вторая производная  меняет знак, то
меняет знак, то 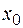 – точка перегиба.
– точка перегиба.
Пример. Найти интервалы выпуклости и точки перегиба функции  .
.
|
|
|
Решение. Найдем первую и вторую производные данной функции:



При  и
и 
 – на этих участках график функции выпуклый вниз. При
– на этих участках график функции выпуклый вниз. При 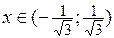
 – на этом участке график функции выпуклый вверх. Точки
– на этом участке график функции выпуклый вверх. Точки 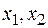 – точки перегиба.
– точки перегиба.
Асимптоты
Определение. Пусть для функции  существует такая прямая, что расстояние от точки
существует такая прямая, что расстояние от точки  графика функции до этой прямой стремится к нулю при бесконечном удалении точки М от начала координат. Тогда такая прямая называется асимптотой графика функции.
графика функции до этой прямой стремится к нулю при бесконечном удалении точки М от начала координат. Тогда такая прямая называется асимптотой графика функции.
Определение. Если при этом координата х точки М стремятся к конечному числу а, то прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
Для существования вертикальной асимптоты в точке  необходимо и достаточно, чтобы хотя бы один из пределов
необходимо и достаточно, чтобы хотя бы один из пределов  был равен бесконечности. Непрерывные функции не имеют вертикальных асимптот.
был равен бесконечности. Непрерывные функции не имеют вертикальных асимптот.
Если же координата х точки М стремится к  или
или  , то мы имеем наклонную асимптоту
, то мы имеем наклонную асимптоту  , для существования которой необходимо и достаточно существование двух пределов
, для существования которой необходимо и достаточно существование двух пределов

При этом указанные пределы могут быть различными при  (для правой наклонной асимптоты) и при
(для правой наклонной асимптоты) и при  (для левой наклонной асимптоты).
(для левой наклонной асимптоты).
Если  (т.е. фактически
(т.е. фактически  ), то мы имеем дело с частным случаем наклонной асимптоты – горизонтальной асимптотой
), то мы имеем дело с частным случаем наклонной асимптоты – горизонтальной асимптотой 
|
|
|
Пример. Найти асимптоты графика функции 
Решение. Функция  имеет единственную точку разрыва
имеет единственную точку разрыва 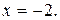

 – вертикальная асимптота.
– вертикальная асимптота.
Далее,

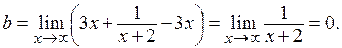
 – наклонная асимптота.
– наклонная асимптота.
Построение графиков функции
Построение графика функции производится по следующей схеме.
1. Находится область определения функции 
2. Определяются характерные особенности функции (четность, нечетность, периодичность, точки пересечения с осями координат, промежутки знакопостоянства).
3. Изучается поведение функции в точках разрыва и на границах области определения (в том числе и на бесконечности). Находятся вертикальные, горизонтальные и наклонные асимптоты.
4. С помощью первой производной находятся точки экстремума и промежутки монотонности.
5. С помощью второй производной находятся точки перегиба и промежутки выпуклости.
6. Строится график функции, который удовлетворяет всем ранее полученным данным. Для более точного построения графика рекомендуется найти несколько контрольных точек.
Пример. Провести полное исследование функции  и построить ее график.
и построить ее график.
1. 
2. Функция не является ни четной, ни нечетной, ни периодической.
 При
При 
 а при
а при 

3.  ,
, 
График функции имеет вертикальную асимптоту  и горизонтальную асимптоту
и горизонтальную асимптоту 
4. 
 При
При 
 , и функция возрастает. При
, и функция возрастает. При 
 , и функция убывает.
, и функция убывает.  – точка максимума,
– точка максимума,  .
.
5. 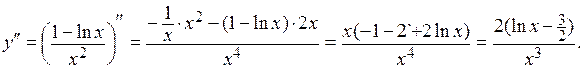
 При
При 
 , и график функции выпуклый вверх. При
, и график функции выпуклый вверх. При 
 , и функция убывает.
, и функция убывает.  – точка перегиба.
– точка перегиба.
6. График функции изображен на рис. 2.



Рис. 2.
Дата добавления: 2019-11-25; просмотров: 115; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
