Способы нахождения производной
Кривые второго порядка
Определение. Уравнение второй степени относительно двух переменных
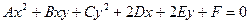
называется общим уравнением кривых второго порядка.
При разных значениях постоянных коэффициентов А, В, С, оно описывает четыре вида линий на плоскости: окружность, эллипс, гиперболу и параболу.
Теорема. Общее уравнение кривой второго порядка всегда определяет: либо окружность (при 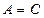 ), либо эллипс (при
), либо эллипс (при 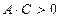 ), либо гиперболу (при
), либо гиперболу (при 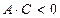 ), либо параболу (при
), либо параболу (при 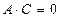 ). При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы — в пару параллельных прямых.
). При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы — в пару параллельных прямых.
Определение. Окружностью называется геометрическое место точек, равноудаленных от данной точки (центра).
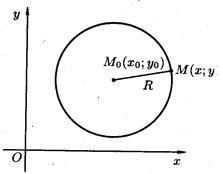
Нормальное уравнение окружности имеет вид
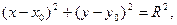
где 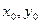 - координаты центра окружности; R- радиус окружности.
- координаты центра окружности; R- радиус окружности.
После раскрытия скобок в этом уравнении получается общее уравнение окружности
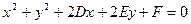 , где
, где 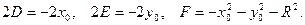
Определение. Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть постоянная величина - 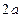 , большая, чем расстояние между фокусами
, большая, чем расстояние между фокусами 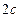 .
.
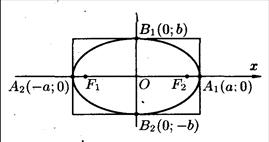
Каноническое уравнение эллипса имеет вид
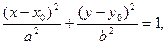
где 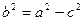 , если
, если 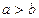 и фокусы находятся на оси
и фокусы находятся на оси 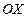 . Параметры
. Параметры 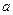 ,
, 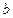 называются полуосями эллипса, а точка
называются полуосями эллипса, а точка 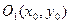 центром эллипса.
центром эллипса.
Определение. Отношение 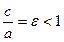 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
|
|
|
Расстояние от точки 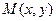 эллипса до его фокусов (фокальные радиусы) находятся по формулам
эллипса до его фокусов (фокальные радиусы) находятся по формулам
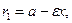
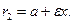
Определение. Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина - 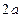 , причем
, причем 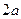 <
< 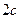 , где
, где 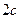 – расстояние между фокусами.
– расстояние между фокусами.
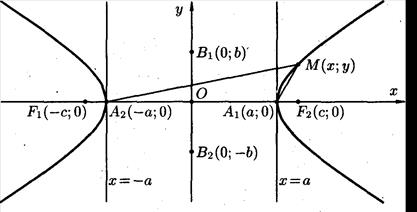
Каноническое уравнение гиперболы, симметричной относительно координат имеет вид
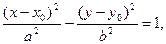
где 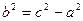 .
.
Параметр 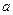 называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр
называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр 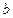 называется мнимой полуосью.
называется мнимой полуосью.
Эксцентриситетом гиперболы называется величина 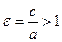 .
.
Расстояние текущей точки М(х, у) гиперболы до фокусов (фокальные радиусы) определяются по формулам
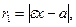
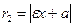 .
.
Прямые, заданные уравнениями 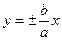 , являются асимптотами гиперболы.
, являются асимптотами гиперболы.
Определение. Параболой называется геометрическое место точек, одинаково удаленных от данной точки- фокуса и данной прямой- директрисы. Расстояние от фокуса до директрисы параболы обозначается через p ( p >0).
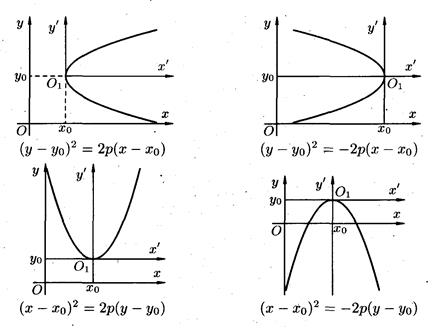
Каноническое уравнение параболы записывается в виде

Точка 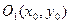 называется вершиной параболы.
называется вершиной параболы.
Фокальный радиус точки М(х, у), т.е. ее расстояние до фокуса на оси Ох, находится по формуле
|
|
|
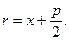
Пример 1. Установить вид кривой второго порядка, заданной уравнением 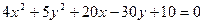 .
.
Решение. Предложенное уравнение определяет эллипс (  ). Действительно, проделаем следующие преобразования:
). Действительно, проделаем следующие преобразования:
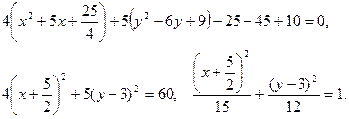
Получилось каноническое уравнение эллипса с центром в 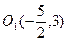 и полуосями
и полуосями 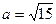 и
и 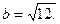
Пример 2. Установить вид кривой второго порядка, заданной уравнением 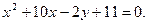
Решение.
Указанное уравнение определяет параболу (С=0). Действительно,
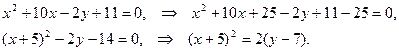
Получилось каноническое уравнение параболы с вершиной в точке 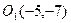 и р=1.
и р=1.
Пример 3. Установить вид кривой второго порядка, заданной уравнением 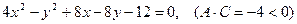 .
.
Решение. Преобразуем уравнение:
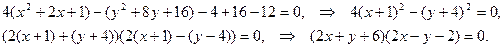 .
.
Это уравнение определяет две пересекающиеся прямые 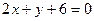 и
и 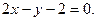
ТЕОРИЯ ПРЕДЕЛОВ
Предел последовательности
Рассмотрим два множества Х и Y.
Определение. Переменная у называется функцией от переменной х (записывается это так: 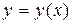 ), если по некоторому закону (правилу) каждому значению х из множества Х поставлено в соответствие одно определенное значение у из множества Y. При этом переменную х называют аргументом функции (или независимой переменной), а переменную у – функцией (зависимой переменной). Множество Х называют областью определения функции, а множество Y – областью значения функции.
), если по некоторому закону (правилу) каждому значению х из множества Х поставлено в соответствие одно определенное значение у из множества Y. При этом переменную х называют аргументом функции (или независимой переменной), а переменную у – функцией (зависимой переменной). Множество Х называют областью определения функции, а множество Y – областью значения функции.
|
|
|
Определение. Числовой последовательностью называется числовая функция, заданная на множестве натуральных чисел.
Числовую последовательность обозначают 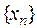 , при этом
, при этом 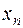 называют элементом последовательности. Последовательность может содержать как конечное, так и бесконечное число элементов.
называют элементом последовательности. Последовательность может содержать как конечное, так и бесконечное число элементов.
Примеры записи соответственно конечной и бесконечной последовательностей:
1) 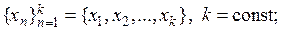
2) 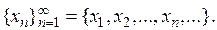
Различают следующие виды числовых последовательностей:
- монотонные;
- немонотонные;
- ограниченные;
- неограниченные.
Определение. Последовательность 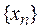 называется монотонно возрастающей, если в ней каждый последующий элемент больше предыдущего:
называется монотонно возрастающей, если в ней каждый последующий элемент больше предыдущего: 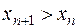 . Например:
. Например: 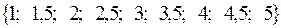 .
.
Аналогичное определение можно дать и для монотонно убывающей последовательности (дайте его самостоятельно).
Определение. Последовательность называется немонотонной, если в ней существует хотя бы два элемента 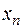 и
и 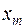 (n > m), что выполняется неравенство
(n > m), что выполняется неравенство 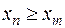 , и хотя бы два элемента
, и хотя бы два элемента 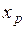 и
и 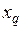 (p > q), для которых выполняется условие
(p > q), для которых выполняется условие 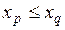 , причем не все элементы равны между собой. Например: {2; 1,5; 4; 7; 9; 10}.
, причем не все элементы равны между собой. Например: {2; 1,5; 4; 7; 9; 10}.
Определение. Последовательность 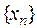 называется ограниченной, если можно указать такое положительное число K, что для всех элементов этой последовательности выполняется неравенство
называется ограниченной, если можно указать такое положительное число K, что для всех элементов этой последовательности выполняется неравенство 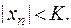 В противном случае она называется неограниченной.
В противном случае она называется неограниченной.
|
|
|
Определение. Последовательность 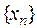 называется ограниченной сверху, если существует такое число k, для которого все элементы последовательности удовлетворяют неравенству
называется ограниченной сверху, если существует такое число k, для которого все элементы последовательности удовлетворяют неравенству 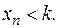
Аналогичное определение ограниченной снизу последовательности предлагается сделать самостоятельно.
Определение. Число А называется пределом последовательности 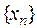 (записывается это так:
(записывается это так: 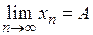 ), если для любого сколь угодно малого положительного значения
), если для любого сколь угодно малого положительного значения 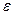 существует такое натуральное число N, зависящее от e, что все элементы данной последовательности, номера которых n > N, удовлетворяют неравенству:
существует такое натуральное число N, зависящее от e, что все элементы данной последовательности, номера которых n > N, удовлетворяют неравенству: 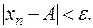
При этом такая последовательность называется сходящейся, в противном случае – расходящейся.
Последнее неравенство можно расписать по определению:
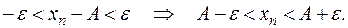
Интервал 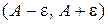 с центром в точке А называют e -окрестностью (эпсилон-окрестностью) этой точки.
с центром в точке А называют e -окрестностью (эпсилон-окрестностью) этой точки.
Геометрически существование предела последовательности означает: какую бы малую окрестность точки А ни взяли, все элементы последовательности 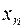 , начиная с некоторого номера
, начиная с некоторого номера 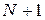 , должны попасть в эту окрестность:
, должны попасть в эту окрестность:
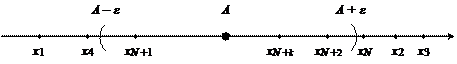
Основные теоремы о пределах
Теорема 1 . Сходящаяся последовательность имеет только один предел.
Теорема 2 . Если 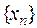 – сходящаяся последовательность, С = const, то
– сходящаяся последовательность, С = const, то
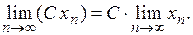
Теорема 3 . Если 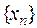 и
и 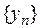 – сходящиеся последовательности, то
– сходящиеся последовательности, то

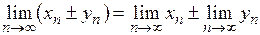 .
.
Теорема 4. Если 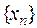 и
и 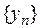 – сходящиеся последовательности, то
– сходящиеся последовательности, то
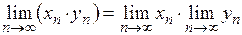 .
.
Теорема 5. Если 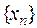 и
и 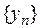 – сходящиеся последовательности и при этом
– сходящиеся последовательности и при этом 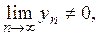 то
то 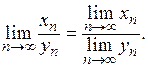
Рассмотрим наиболее часто встречающиеся приемы вычисления пределов последовательностей.
Пример 1. 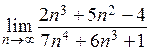 .
.
Решение. При подстановке предельного значения получаем выражение, символически обозначаемое 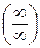 , являющееся неопределенностью.
, являющееся неопределенностью.
Степень многочлена в знаменателе равна четырем. Поэтому вынесем из числителя и знаменателя 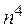 и сократим дробь
и сократим дробь
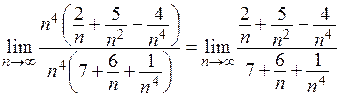 .
.
Применяя основные теоремы о пределах и учитывая, что предел каждой из дробей 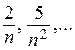 , в числителе которой константа, а в знаменателе
, в числителе которой константа, а в знаменателе 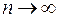 , равен нулю, получим
, равен нулю, получим 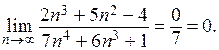
Пример 2. 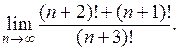
Решение. Напомним, что символом 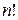 (эн-факториал) обозначается произведение всех натуральных чисел от 1 до п:
(эн-факториал) обозначается произведение всех натуральных чисел от 1 до п: 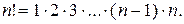 Например,
Например, 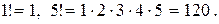 Кроме того, полагается, что
Кроме того, полагается, что 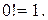
Распишем факториалы:
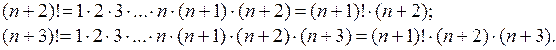
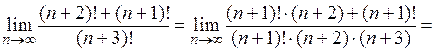
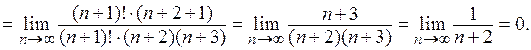
Пример 3. 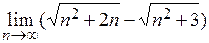 .
.
Решение. При подстановке предельного значения получаем выражение, символически обозначаемое 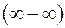 , являющееся неопределенностью. Выполним тождественное преобразование выражения данного примера и используем соответствующие теоремы о сходящихся последовательностях:
, являющееся неопределенностью. Выполним тождественное преобразование выражения данного примера и используем соответствующие теоремы о сходящихся последовательностях:
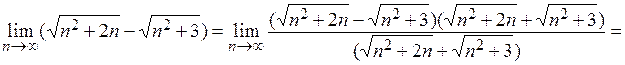
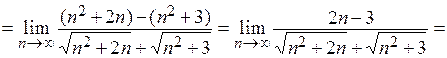
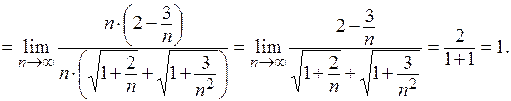
Замечание. Проделанная операция избавления от радикалов в числителе называется умножением на сопряженное выражение и опирается на формулы сокращенного умножения (вспомните их!). Если выражение для 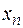 имеет вид
имеет вид 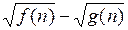 , то решение задачи в большинстве случаев нужно начинать с домножения его на
, то решение задачи в большинстве случаев нужно начинать с домножения его на 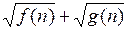 (и, разумеется, одновременно поделить его на то же самое выражение). Если же выражение для
(и, разумеется, одновременно поделить его на то же самое выражение). Если же выражение для  имеет вид
имеет вид 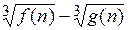 , то помогает умножение на выражение вида
, то помогает умножение на выражение вида 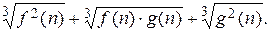 Для выражения вида
Для выражения вида 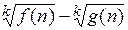 в общем случае сопряженным будет
в общем случае сопряженным будет
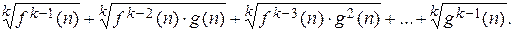
Пример 4. 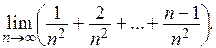
Решение. Выполним ряд тождественных преобразований:
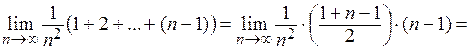
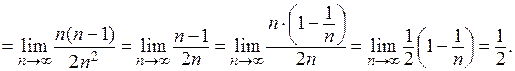
Пример 5. 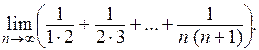
Решение. Рассмотрим дробь 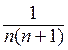 , которую можно представить в виде:
, которую можно представить в виде: 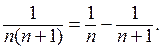 С учетом последнего, выражение данного предела принимает вид:
С учетом последнего, выражение данного предела принимает вид:
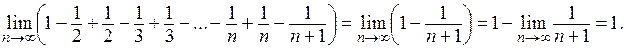
Предел функции
Рассмотрим функцию 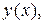 определенную в некоторой окрестности точки a, за исключением, быть может, самой точки a.
определенную в некоторой окрестности точки a, за исключением, быть может, самой точки a.
Определение. Число А называется пределом функции 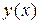 при х, стремящемся к а, если для любого сколь угодно малого положительного числа
при х, стремящемся к а, если для любого сколь угодно малого положительного числа 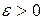 существует такое (зависящее от e) число
существует такое (зависящее от e) число 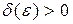 , что для всех
, что для всех 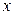 , удовлетворяющих условию
, удовлетворяющих условию 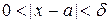 выполняется неравенство
выполняется неравенство 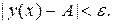
В этом случае пишут: 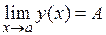 .
.
Если 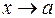 и при этом
и при этом 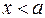 , то говорят, что «х стремится к а слева», и пишут:
, то говорят, что «х стремится к а слева», и пишут: 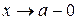 . Если
. Если 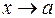 и при этом
и при этом 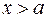 , то говорят, что «х стремится к а справа», и пишут:
, то говорят, что «х стремится к а справа», и пишут: 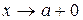 . Пределы
. Пределы 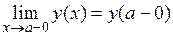 и
и 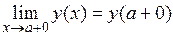 называют соответственно пределом функции
называют соответственно пределом функции 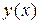 в точке а слева и справа (если они существуют).
в точке а слева и справа (если они существуют).
Теорема. Для того чтобы функция 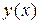 в точке а имела предел, необходимо и достаточно существование односторонних пределов функции
в точке а имела предел, необходимо и достаточно существование односторонних пределов функции 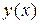 , равных между собой:
, равных между собой: 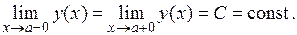
Определение. Число А называется пределом функции 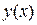 при х стремящемся к ¥
при х стремящемся к ¥ 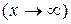 , если для любого сколь угодно малого положительного числа e можно указать число
, если для любого сколь угодно малого положительного числа e можно указать число 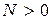 , что для всех значений х, удовлетворяющих неравенству
, что для всех значений х, удовлетворяющих неравенству 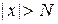 , будет выполняться неравенство
, будет выполняться неравенство 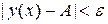 .
.
При этом пишут: 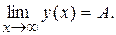
Аналогичные определения существуют при 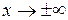 (дайте их самостоятельно).
(дайте их самостоятельно).
Определение. Функция 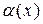 называется бесконечно малой величиной при
называется бесконечно малой величиной при 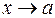 , если для любого сколь угодно малого положит значения
, если для любого сколь угодно малого положит значения 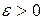 , существует такое положительное число
, существует такое положительное число 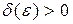 , что для всех х, удовлетворяющих условию
, что для всех х, удовлетворяющих условию 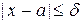 , выполняется неравенство
, выполняется неравенство 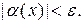
В этом случае пишут 
Основные теоремы о пределах
Теорема 1 . Предел суммы двух функций 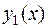 и
и 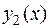 , при
, при 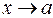
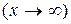 равен сумме пределов от каждой из этих функций:
равен сумме пределов от каждой из этих функций:

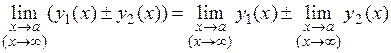 .
.
Теорема справедлива для любого конечного числа функций.
Теорема 2 . Предел произведения двух функций 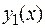 и
и 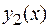 , при
, при 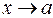
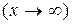 равен произведению пределов каждой из данных функций:
равен произведению пределов каждой из данных функций:
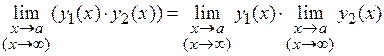 .
.
Теорема справедлива для любого конечного числа функций.
Теорема 3 . Предел частного двух функций 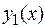 и
и 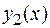 при
при 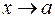
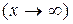 равен частному пределов этих функций:
равен частному пределов этих функций:
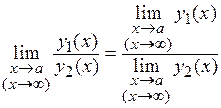 , если
, если 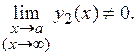
Замечательные пределы
Первый замечательный предел: 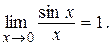
Второй замечательный предел: 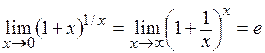 .
.
Здесь число е – основание натурального логарифма: 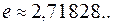
Определение. Функция 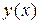 называется непрерывной в точке
называется непрерывной в точке 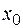 , если она определена в данной точке и некоторой ее окрестности и
, если она определена в данной точке и некоторой ее окрестности и
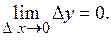
Т.е. 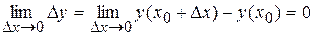 или
или
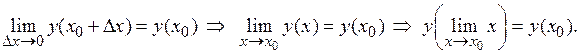
Последнее соотношение означает предельный переход под знаком непрерывной функций, который может быть использован при вычислении пределов.
Определение. Точка 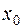 называется точкой разрыва функции
называется точкой разрыва функции 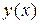 , если выполняется по крайней мере одно из условий:
, если выполняется по крайней мере одно из условий:
1. Функция 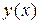 не определена в точке
не определена в точке 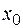 .
.
2. Односторонние пределы функции 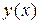 в данной точке не равны между собой:
в данной точке не равны между собой: 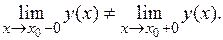
3. Хотя бы один из односторонних пределов не равен значению функции в точке 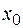 :
: 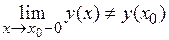 или
или 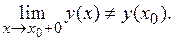
4. Не существует предела функции 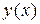 в точке
в точке 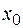 .
.
Функция 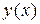 , непрерывная в каждой точке некоторого интервала
, непрерывная в каждой точке некоторого интервала 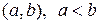 , называется непрерывной на интервале
, называется непрерывной на интервале 
Классификация точек разрыва:
1. Точка устранимого разрыва, в которой оба односторонних предела существуют и равны: 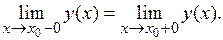
2. Точка разрыва первого рода, в которой оба односторонних предела существуют, но не равны: 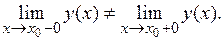
3. Во всех остальных случаях точка 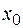 называется точкой разрыва второго рода. Это могут быть точки, в которых по крайней мере один из односторонних пределов либо бесконечен, либо не существует.
называется точкой разрыва второго рода. Это могут быть точки, в которых по крайней мере один из односторонних пределов либо бесконечен, либо не существует.
Две бесконечно малые величины 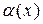 и
и 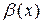 называются эквивалентными при
называются эквивалентными при 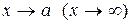 , если
, если 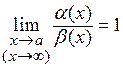 . Пишут:
. Пишут: 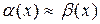 .
.
При вычислении пределов часто используют таблицу эквивалентных бесконечно малых величин при 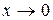 .
.
Таблица эквивалентных бесконечно малых величин
1) 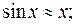
| 4) 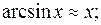
| 7) 
|
2) 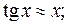
| 5) 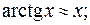
| 8) 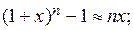
|
3) 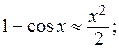
| 6) 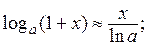
| 9) 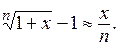
|
В простейшем случае вычисление предела сводится к подстановке предельного значения аргумента в выражение предела. Однако чаще всего при этом получаются неопределенности одного из следующих видов:
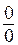 ,
, 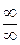 ,
, 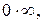
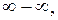
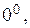
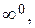
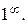
Вычисление предела в этих случаях называют раскрытием неопределенности.
Пример 1. 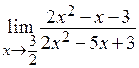 .
.
Решение. Выражения числителя и знаменателя являются многочленами, а при подстановке предельного значения в условие получаем неопределенность вида 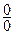 . Это говорит о том, что
. Это говорит о том, что 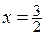 является корнем как числителя, так и знаменателя, т.е. числитель и знаменатель могут быть разложены на множители. Произведем разложение этих выражений. Для этого найдем корни уравнений
является корнем как числителя, так и знаменателя, т.е. числитель и знаменатель могут быть разложены на множители. Произведем разложение этих выражений. Для этого найдем корни уравнений 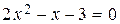 и
и 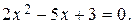
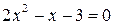

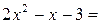
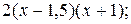
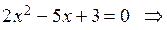
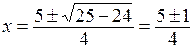
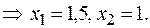
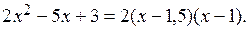
Подставим полученные разложения в выражение предела:
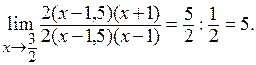
Пример 2. 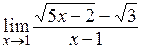 .
.
Решение. В данном примере также имеем неопределенность вида 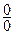 . Наличие радикалов предполагает преобразования, связанного с умножением дроби на выражение, сопряженное к числителю:
. Наличие радикалов предполагает преобразования, связанного с умножением дроби на выражение, сопряженное к числителю:
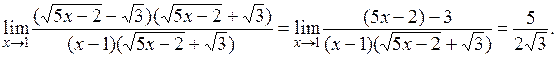
Пример 3. 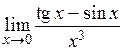 .
.
Решение. В данном примере при подстановке предельного значения получим неопределенность вида 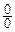 . Выражение данного предела предполагает наличие в нем первого замечательного предела либо применения эквивалентных бесконечно малых величин:
. Выражение данного предела предполагает наличие в нем первого замечательного предела либо применения эквивалентных бесконечно малых величин:
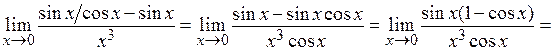
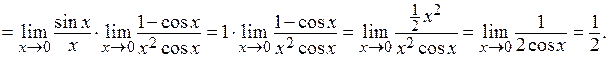
Пример 4. 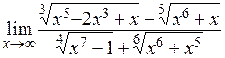 .
.
Решение. При подстановке предельного значения получаем неопределенность 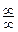 . Конструкция данного выражения предполагает следующий способ раскрытия неопределенности. Выбираем наивысшую степень переменной, входящую в выражение данного предела. Для этого надо выбрать наибольшее значение из следующих чисел:
. Конструкция данного выражения предполагает следующий способ раскрытия неопределенности. Выбираем наивысшую степень переменной, входящую в выражение данного предела. Для этого надо выбрать наибольшее значение из следующих чисел: 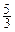 ,
, 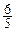 ,
, 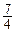 и 1, которые являются наибольшими степенями переменных, входящих в выражение числителя и знаменателя. Наибольшим значением является
и 1, которые являются наибольшими степенями переменных, входящих в выражение числителя и знаменателя. Наибольшим значением является 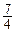 . Делим числитель и знаменатель данного выражения на
. Делим числитель и знаменатель данного выражения на 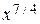 :
:
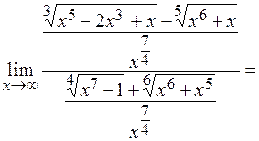
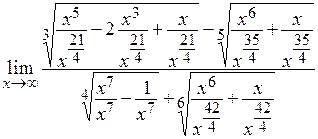 =
=
= 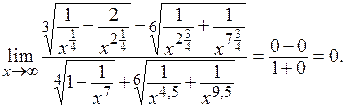
Пример 5. 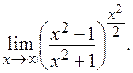
Решение. При подстановке предельного значения получаем неопределенность вида 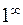 . Конструкция данного предела предполагает наличие второго замечательного предела. С помощью тождественных преобразований выделяем второй замечательный предел:
. Конструкция данного предела предполагает наличие второго замечательного предела. С помощью тождественных преобразований выделяем второй замечательный предел:
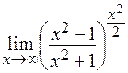 =
= 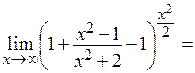
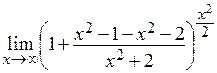 =
=
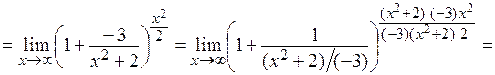
= 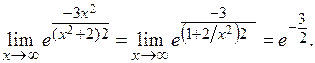
Пример 6. 
Решение. При подстановке предельного значения переменной в выражение данного предела получаем неопределенность 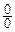 . Преобразуем числитель данной дроби по свойству логарифмической функции и применим к выражению числителя таблицу эквивалентных бесконечно малых функций:
. Преобразуем числитель данной дроби по свойству логарифмической функции и применим к выражению числителя таблицу эквивалентных бесконечно малых функций:
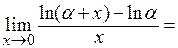
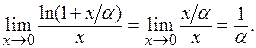
ПРОИЗВОДНАЯ
Рассмотрим функцию 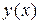 , заданную на некотором промежутке. Дадим аргументу x приращение
, заданную на некотором промежутке. Дадим аргументу x приращение 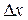 , тогда функция
, тогда функция 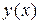 получит приращение
получит приращение
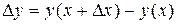 .
.
Определение. Производной функции называется предел отношения приращения функции 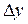 к приращению аргумента
к приращению аргумента 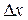 , когда последнее произвольным образом стремится к нулю. Операция нахождения производной называется дифференцированием. Производная функции – это тоже функция.
, когда последнее произвольным образом стремится к нулю. Операция нахождения производной называется дифференцированием. Производная функции – это тоже функция.
Производная обозначается следующим образом: 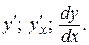
По определению, при любом допустимом х: 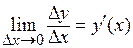 .
.
Таблица производных
1) 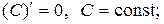
| 6) 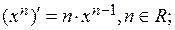
| 11) 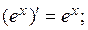
|
2) 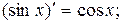
| 7) 
| 12) 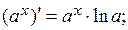
|
3) 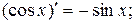
| 8) 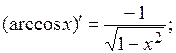
| 13) 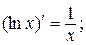
|
4) 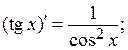
| 9) 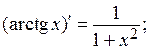
| 14) 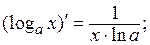
|
5) 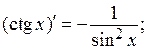
| 10) 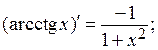
|
Правила дифференцирования
1. 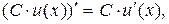 где
где 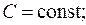
2. 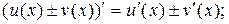
3. 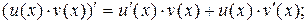
4. 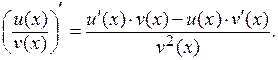
Способы нахождения производной
1. Если функция является сложной: 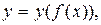 то
то 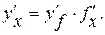
2. Если функция задана параметрически: 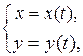 то
то 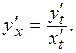
3. Если функция задана неявно: 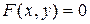 , то
, то 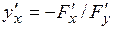 .
.
Чаще для нахождения производной от функции, заданной неявно, применяют не саму вышеприведенную формулу, а процедуру ее нахождения (см. ниже пример 5). Заметим, что при нахождении 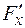 переменную y нужно считать постоянной величиной.
переменную y нужно считать постоянной величиной.
4. Для нахождения производной от сложной функции, имеющей вид: 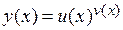 , предварительно применяют операцию логарифмирования, в результате которой получаем:
, предварительно применяют операцию логарифмирования, в результате которой получаем:
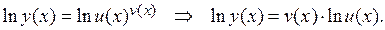
Дифференцируем последнее равенство по х:
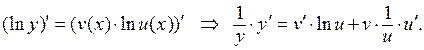
Из этого равенства находим 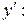
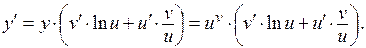
Производные высших порядков
Определение. Производной второго порядка от функции 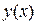 называется производная от производной
называется производная от производной 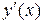 функции
функции 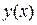 :
: 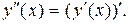 Вторая производная может обозначается следующим образом:
Вторая производная может обозначается следующим образом:
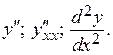
Определение. Производной n-го порядка от функции 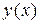 называется производная от производной
называется производная от производной 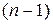 -го порядка:
-го порядка:
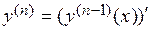 или
или 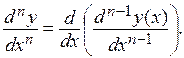
При нахождении производных от заданных функций в первую очередь необходимо установить способ задания функции. Затем, в зависимости от сложности функции, применяем соответствующую формулу и правила дифференцирования.
Пример 1. 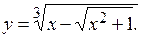
Решение. Эта функция задана явно, по структуре является сложной. Представим эту функцию в виде степенной
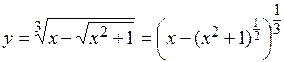
и применим формулу производной от сложной функции и правила дифференцирования:
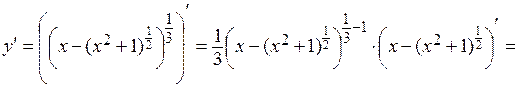
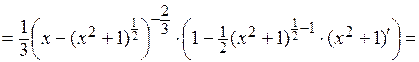
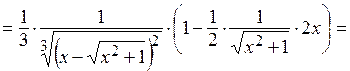
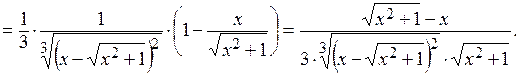
Пример 2. 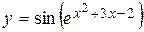 .
.
Решение. Применяем формулу производной от сложной функции:
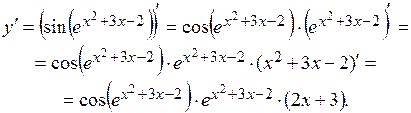
Пример 3. 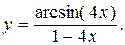
Решение. Применяя формулу производной частного, получаем:
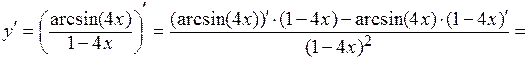
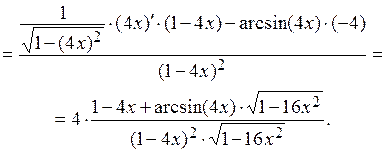
Пример 4. 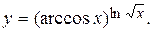
Решение. Данная функция является сложной: одновременно показательной и степенной. Поэтому для нахождения производной от этой функции в начале ее логарифмируем:
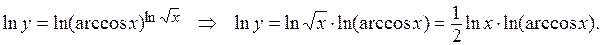
Дифференцируем последнее равенство с учетом того, что 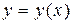 , получаем:
, получаем:
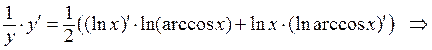
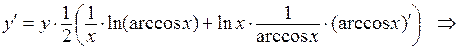

Пример 5. 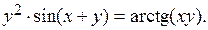
Решение. В данном случае функция задана неявно. Дифференцируем заданную функцию с учетом того, что 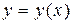 :
:
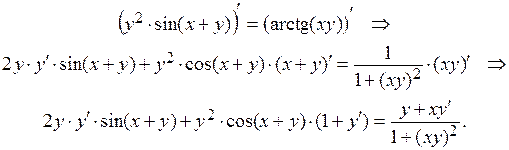
Рассматривая это равенство как уравнение относительно 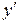 , получаем:
, получаем:
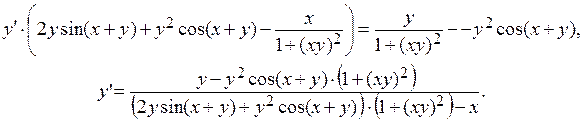
Пример 6. 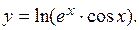
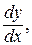
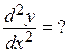
Решение. Применяем формулу производной от сложной функции:
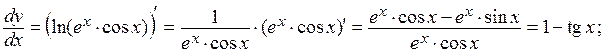
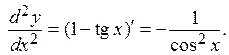
Замечание. Для упрощения вычислений можно предварительно преобразовать данную функцию: 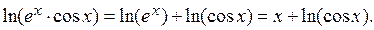
Пример 7. 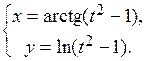
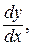
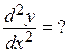
Решение. Функция задана параметрически. Применяем формулу производной о функции заданной параметрически:
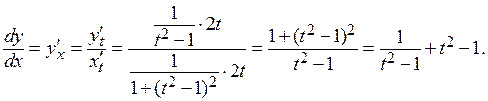
Вычисляем производную второго порядка от функции, заданной параметрически:
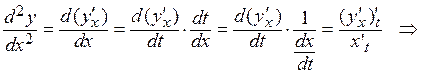
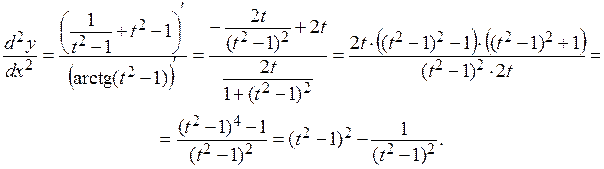
Дата добавления: 2019-11-25; просмотров: 146; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
