Метод симметричных составляющих в релейной защите

Общие положения

Изучение и анализ трехфазных энергосистем в условиях различного рода повреждений, действующих в них напряжений, токов и фазовых соотношений между ними требуют применения метода симметричных составляющих. Поэтому в настоящем разделе будут рассмотрены основные понятия метода симметричных составляющих и его применение в РЗ.

Известно, что любая несимметричная система трех векторов может быть показана в виде суммы систем векторов:

· симметричной системы векторов прямой последовательности (ПП);

· симметричной системы векторов обратной последовательности (ОП);

· системы синфазных векторов нулевой последовательности (НП).

Системы векторов ПП, ОП и НП называют симметричными составляющими исходной несимметричной системы полных векторов.

В качестве обобщенного примера рассмотрим несимметричную систему полных векторов А, В, С (рисунок 2.1) В общем случае она будет содержать составляющие ПП, ОП, НП.

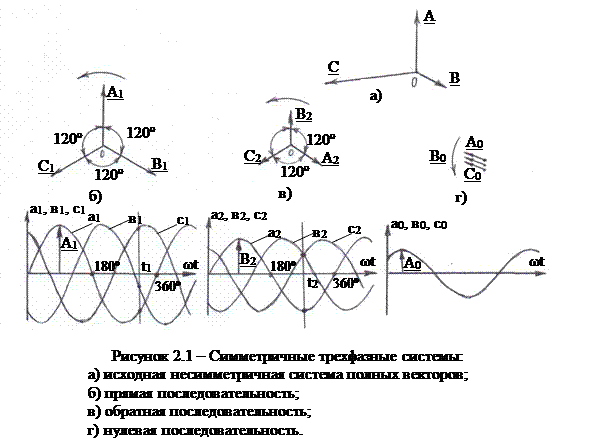Принято вращение всех векторов последовательностей против часовой стрелки.

Общим свойством систем прямой и обратной последовательностей является то, что в любой момент времени сумма мгновенных значений синусоидальных кривых всех трех фаз данной последовательности равна нулю с учетом знаков (рисунки 2.1, б) и в). Например, в момент времени t₁ (рисунок 2.1, б) сумма +с₁ +(– в₁) + (– а₁) = 0.

Также геометрические суммы векторов А₁, В₁, С₁ и А₂, В₂, С₂ равны нулю, то есть

А₁+ В₁+ С₁ = 0 и А₂+ В₂+ С₂ =0. (2.1)

Если известны векторы симметричных составляющих трехвекторной несимметричной (а также симметричной) исходной системы полных векторов, то значения фазных полных векторов А, В, С получают как геометрические суммы одноименных векторов всех трех последовательностей, то есть

А = А₁+ А₂+ А₀; В = В₁+ В₂+ В₀; С = С₁+ С₂+ С₀ . (2.2)

2.2 Оператор аи его свойства

Любой из векторов симметричной трехфазной системы может быть выражен с помощью вектора другой фазы той же системы, если воспользоваться вспомогательным оператором – комплексным множителем, представляющим собой комплексное число вида : а = е^j^120º или

а = -0,5 + j0,87. Оператор а называют еще фазовым множителем, так как умножение вектора на оператор а означает поворот этого вектора на 120º против часовой стрелки.

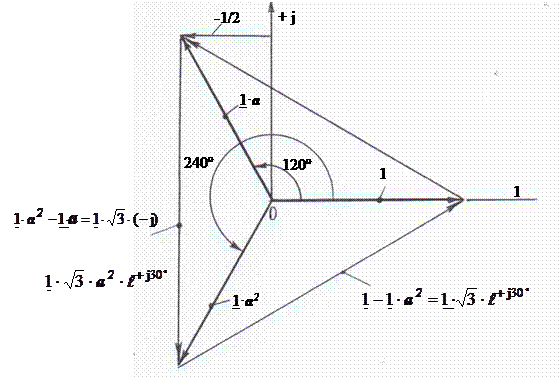
На рисунке 2.2 показаны дополнительные комплексные множители, полученные с помощью несложных математических действий над оператором а. Для наглядности эти дополнительные множители изображены в виде векторов. Наиболее часто применяются следующие множители: а; а²; 1, где а² = а · а;1 = а² · а = а · а · а ·= а³.

С учетом множителей (рисунок 2.2) система векторов ПП А₁, В₁, С₁ представленная на рисунке 2.1 может быть выражена с помощью одного вектора, например, А₁ и операторов а и а², то есть

А₁, А₁· а², А₁· а, что равносильно А₁, В₁, С₁ (2.3)

Аналогично получим систему векторов ОП А₂, В₂, С₂

А₂, А₂· а, А₂· а². (2.4)

или

Рисунок 2.2 Комплексные множители, создаваемые на базе оператора а

Пользуясь этими и подобными им зависимостями, можно представить полные векторы А, В, Слюбой несимметричной системы с помощью векторов систем симметричных составляющих, образующих исходную несимметричную систему. Причем за основу можно взять как векторы фазы А, так и векторы фаз В и С.

А B C