Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.

ПРОИЗВОДНЫЕ ЕДИНИЦЫ

ПРОСТРАНСТВО И ВРЕМЯ

Площадь S — величина, характеризующая геометрические фигуры на плоскости и на искривленной поверхности и определяемая в простейших случаях числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины; dim S = L², единица — квадратный метр ( m ² ; м²).

Квадратный метр равен площади квадрата со сторонами, длины которых равны 1 м.

Объем, вместимость V — величина, характеризующая геометрические тела и определяемая в простейших случаях числом умещающихся в теле единичных кубов, т. е. кубов с ребром , равным в единице длины; dim V=L³, единица — кубический метр ( m ³ , м³).

Кубический метр равен объему куба с ребрами, длины которых равны 1 м.

Скорость v — величина[5], равная первой производной от перемещения по времени:

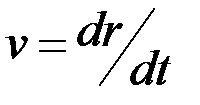
dim a = LT^-1, единица — метр в секунду (m/s; м/с).

Метр в секунду равен скорости прямолинейно и равномерно движущейся точки, при которой эта точка за время 1 с перемещается на расстояние 1 м.

Ускорение а — величина, равная первой производном от скорости по времени

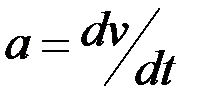
dim a=LT^-2, единица — метр на секунду в квадрате (m/s²; м/с²).

Метр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки изменяется на 1 м/с.

Угловая скорость ω — величина, равная первой производной от угла поворота по времени:

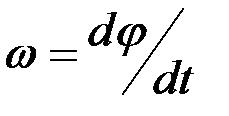
dim ω = T^-1 единица — радиан в секунду (rad/s; рад/с) .

Радиан в секунду равен угловой скорости равномерно вращающегося тела, все точки которого за время 1 с поворачиваются относительно оси на угол 1 рад.

Угловое ускорение ε— величина, определяемая первой производной от угловой скорости по времени:

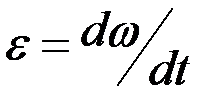
Dim ε = Т^-2 , единица-радиан на секунду в квадрате (rad/s²; рад/с²).

Радиан на секунду в квадрате равен угловому ускорению равноускоренно вращающегося тела, при котором оно за время 1 с изменяет угловую скорость на 1 рад/с.

ПЕРИОДИЧЕСКИЕ И СВЯЗАННЫЕ С НИМИ ЯВЛЕНИЯ

Фаза колебаний φ— аргумент функции, описывающей величину, изменяющуюся по закону гармонических колебаний. Фаза колебаний не имеет размерности, единица — радиан (rad; рад),

Период Т — интервал времени, в течение которого совершается один цикл периодического процесса; dim Т = Т, единица — секунда (s, с).

Частота периодического процесса ƒ, ν — величина обратная периоду; dim ν = T^-1, единица — герц (Hz; Гц).

Герц равен частоте периодического процесса, при которой за время 1 с совершается один цикл периодического процесса.

Частота вращения n — величина, равная числу оборотов, совершаемых за время 1 с; dim n = T^-1, единица — секунда в минус первой степени (s^-1; c^-1).

Секунда в минус первой степени равна частоте равномерного вращения, при которой за время 1 с тело совершает один полный оборот.

Волновое число ν — величина, обратная длине волны λ:

dim v = L^-1, единица — метр в минус первой степени ( m ^-1 ; м^-1).

Метр в минус первой степени равен волновому числу колебаний с длиной волны 1 м.

Коэффициент затухания δ — величина, обратная интервалу τ, в течение которого амплитуда А уменьшается в е раз; dim δ = Т^-1, единица — секунда в минус первой степени (s^-1; c^-1).

Секунда в минус первой степени равна коэффициенту затухания, при котором за время 1 с амплитуда уменьшается в е раз, где е — основание натурального логарифма.

Коэффициент ослабления μ — величина, характеризующая свойства вещества и равная отношению относительного уменьшения интенсивности излучений к длине пути , пройденного излучением в данном веществе:

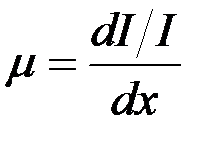
dim μ = L^-1, единица — метр в минус первой степени ( m ^-1 ; м^-1).

Метр в минус первой степени равен коэффициенту ослабления, при котором на расстоянии в 1 м амплитуда уменьшается в е раз, где е — основание натурального логарифма.

МЕХАНИКА

Плотность ρ— величина, равная отношению массы dm элемента тела к объему dV этого элемента:

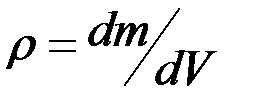
dim ρ= ML^-3, единица — килограмм на кубический метр (kg/m³; кг/м³).

Килограмм на кубический метр равен плотности однородного вещества, масса которого при объеме 1 м³ равна 1 кг.

Удельный объем υ — величина, равная отношению объема dV элемента тела к массе dm этого элемента:

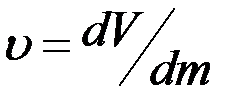
dim υ = L³ M^-1, единица — кубический метр на килограмм (m³ /kg; м³ /кг).

Кубический метр на килограмм равен удельному объему однородного вещества, объем которого при массе 1 кг равен 1 м³.

Импульс (количество движения) материальной точки — величина, равная произведению массы m материальной точки на ее скорость v.

dim p=LMT^-1, единица — килограмм-метр в секунду (kg∙m/s; кг∙м/с).

Килограмм-метр в секунду равен импульсу материальной точки массой 1 кг, движущейся со скоростью 1 м/с.

Момент импульса (момент количества движения) L точки, вращающейся вокруг неподвижной оси, — величина, равная произведению импульса точки на расстояние ее до оси вращения:

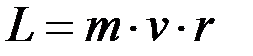
dim L = L² MT^-1, единица — килограмм-метр в квадрате на секунду (kg∙m²/s; кг∙м²/с).

Килограмм-метр в квадрате на секунду равен моменту импульса материальной точки, движущейся по окружности радиусом 1 м и имеющей импульс 1 кг∙м/с.

Момент инерции (динамический момент инерции) материальной точки относительно некоторой оси — величина, равная произведению массы m материальной точки на квадрат расстояния r ее до оси вращения:

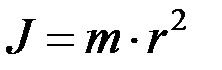
dim J = M L2, единица (kg∙m²; кг ∙ м ² ).

Килограмм-метр в квадрате равен моменту инерции материальной точки массой 1 кг, находящейся на расстоянии 1 м от оси вращения.

Сила F — векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел. Определяется по второму закону Ньютона:

dim F = LMT^-2, единица — ньютон (N; Н).

Ньютон равен силе, придающей телу массой 1 кг ускорение 1 м/с² в направлении действия силы.

Момент силы М относительно некоторой точки — величина, равная произведению силы F на плечо h, т. е. на расстояние между направлением силы и этой точкой:

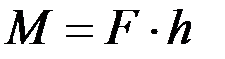
dim M = L² MT^-2, единица — ньютон-метр (N∙m; Н∙м).

Ньютон-метр равен моменту силы, равной 1 Н, относительно точки, расположенной на расстоянии 1 м от линии действия силы.

Импульс силы I — величина, равная произведению силы F на интервал времени, в течение которого сила действовала:

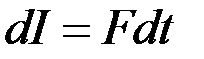
dim I = LMT^-1, единица — ньютон-секунда (N-s; H-c).

Ньютон-секунда равна импульсу силы, равной 1 Н и действующей в течение 1 с.

Давление P — величина, равная отношению силы dF, действующей на элемент поверхности нормально к ней, к площади dS этого элемента:

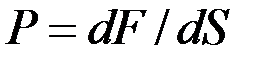
dim P = L^-1 M T ^-2, единица — паскаль (Ра; Па).

Паскаль [6] равен давлению, вызываемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м².

Динамическая вязкость η является коэффициентом пропорциональности в формуле силы внутреннего трения:

где dv/dl — градиент скорости; ∆S — площадь поверхности слоя, на которую рассчитывается сила внутреннего трения; dim η = L^-1 MT^-1 , единица — паскаль-секунда (Pa∙s; Па∙с).

Паскаль-секунда равна динамической вязкости среды, касательное напряжение в которой при ламинарном течении и при разности скоростей слоев, находящихся на расстоянии 1 м по нормали к направлению скорости 1 м/с, равно 1 Па.

Кинематическая вязкость ν — величина, равная отношению динамической вязкости среды к ее плотности:

dim v = L² T^-1, единица — квадратный метр на секунду (m²/s; м²/с).

Квадратный метр на секунду равен кинематической вязкости среды с динамической вязкостью 1 Па∙с и плотностью 1 кг/м³.

Поверхностное натяжение α жидкости — величина, равная отношению силы dF, действующей на участок контура свободной поверхности нормально к контуру и по касательной к поверхности, к длине dl этого участка:

dim α = МТ ^-2, единица — ньютон на метр (N/m; Н/м).

Ньютон на метр равен поверхностному натяжению жидкости, создаваемому силой 1 Н, действующей на участок контура свободной поверхности длиной 1 м нормально к контуру и по касательной к поверхности.

Работа. Элементарной работой dA называют величину, равную скалярному произведению силы F на элементарное перемещение ds:

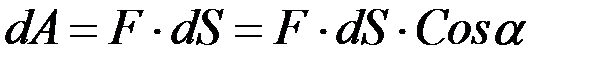
dim A = L ² МТ^-2, единица — джоуль (J; Дж).

Джоуль [7] равен работе силы 1 Н, перемещающей тело на расстояние 1 м в направлении действия силы.

Мощность N, Р — величина, равная отношению работы dA к бесконечно малому интервалу времени dt, в течение которого эта работа совершается:

N=dAldt;

dim N =L² MT^-3, единица — ватт (W; Вт).

Ватт равен мощности, при которой работа в 1 Дж производится за время 1 с.

ТЕПЛОТА

Температурный коэффициент — величина, равная отношению относительного изменения dX/X₀ физической величины к изменению dT температуры от принятой за начальную:

где Х₀ — значение физической величины при температуре, принятой за начальную; dim a = Ө^-1, единица — кельвин в минус первой степени (К^-1; К^-1);

Кельвин в минус первой степени равен температурному коэффициенту относительного изменения физической величины, при котором изменение температуры на 1 К от принятой за начальную вызывает относительное изменение этой величины, равное единице.

Температурный градиент grad Т — векторная величина, численно равная изменению температуры на единице длины и направленная в сторону наиболее быстрого изменения температуры температурного поля;

dim grad T = L^-1 Ө, единица — кельвина на метр (К/т; К/м).

Кельвин на метр равен температурному градиенту поля, в котором на участке длиной 1 м в направлении градиента температура изменяется на 1 К.

Внутренняя энергия U системы — энергия хаотического теплового движения всех микрочастиц системы (молекул, атомов, ионов и т. п.) и энергия взаимодействия этих частиц.

Внутренняя энергия, как и любая другая энергия, имеет размерность работы: dim U = L²MT^-2 и выражается в джоулях (J; Дж).

Теплота, количество теплоты Q — часть внутренней энергии, которая самопроизвольно, без внешнего воздействия переходит от тел более нагретых к телам менее нагретым посредством теплопроводности или лучеиспускания; dim Q = L² MT^-2, единица — джоуль (J; Дж).

Джоуль [8] равен количеству теплоты, эквивалентному работе 1 Дж

Тепловой поток Ф через некоторую поверхность — величина, равная отношению количества теплоты dQ, прошедшей через эту поверхность, ко времени dt, за которое прошло это количество теплоты:

Размерность теплового потока равна размерности мощности: dim Ф = L² MT^-3, единица — ватт (W, Вт).

Ватт равен тепловому потоку, эквивалентному механической мощности 1 Вт.

Поверхностная плотность теплового потока q — величина, равная отношению теплового потока d Ф к площади dS поверхности, через которую проходит этот поток:

dim q = MT^-3, единица — ватт на квадратный метр (W/m²; Вт/м²).

Ватт на квадратный метр равен поверхностной плотности теплового потока, при которой тепловой поток 1 Вт равномерно распределен по поверхности площадью 1 м².

Коэффициент теплопроводности λ, — величина, равная плотности теплового потока, обусловленного теплопроводностью при градиенте температуры, равном единице. Входит в качестве коэффициента в формулу, определяющую количество теплоты, перенесенное за время t через поверхность площадью S в направлении нормали к этой поверхности:

где dT/dx — градиент температуры; dim λ, = LMT^-3 Ө^-1, единица — ватт на метр-кельвин (W/(m∙K); Вт/(м-К)).

Ватт на метр-кельвин равен коэффициенту теплопроводности вещества, в котором при стационарном режиме с поверхностной плотностью теплового потока 1 Вт/м² устанавливается температурный градиент 1 К/м.

Теплоемкость С тела (системы) — величина, равная отношению количества теплоты dQ, необходимой для нагревания тела (системы тел), к разности температур dT тела:

dim C=L² MT^-2 Ө^-1, единица — джоуль на кельвин (J/K; Дж/К).

Джоуль на кельвин равен теплоемкости системы, температура которой повышается на 1 К при подведении к системе количества теплоты 1 Дж.

Удельная теплоемкость с вещества — величина, равная отношению теплоемкости соднородного тела (системы) к его массе:

dim c = L² T^-2 Ө^-1, единица — джоуль на килограмм-кельвин (J/(kg∙K); Дж/(кг∙К)).

Джоуль на килограмм-кельвин равен удельной теплоемкости вещества, имеющего при массе 1 кг теплоемкость 1 Дж/К.

Температуропроводность α— величина, характеризующая скорость выравнивания температуры при нестационарной теплопроводности и равная отношению коэффициента теплопроводности λ. к объемной теплоемкости с_р∙ρ вещества:

где Ср — удельная теплоемкость вещества при постоянном давлении; ρ— плотность вещества; dim α=L² T^-1, единица — квадратный метр на секунду (m²/s; м²/с).

Квадратный метр на секунду равен температуропроводности вещества с коэффициентом теплопроводности 1 Вт/ (м∙ К), удельной теплоемкостью при постоянном давлении

1Дж/(кг∙К) и плотностью 1 кг/м³.

Удельная газовая постоянная В — величина, равная отношению работы dA, совершаемой идеальным газом при изобарном нагревании, к массе газа m и интервалу температур dT, на который газ нагревается:

dim B = L² T^-2 Ө^-1, единица — джоуль на килограмм-кельвин (J/(kg∙K); Дж/(кг∙К)).

Джоуль на килограмм-кельвин равен удельной газовой постоянной идеального газа массой 1 кг, совершающего при повышении температуры на 1 К при постоянном давлении работу 1 Дж.

Энтропия S системы — однозначная функция состояния системы, определяемая соотношением

где dQ — бесконечно малое количество теплоты, сообщенной системе при температуре Т; dim d Q = L² MT^-2 Ө^-1, единица — джоуль на кельвин (J/K; Дж/К).

Джоуль на кельвин равен изменению энтропии системы, которой при температуре пК в изотермическом процессе сообщается количество теплоты n Дж.

Удельная энтропия s — величина, равная отношению энтропии dS к массе dm системы:

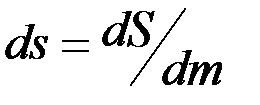
dim s = L² T^-2 Ө^-1, единица — джоуль на килограмм-кельвин (J/(kg∙K): Дж/(кг∙К)).

Джоуль на килограмм-кельвин равен удельной энтропии вещества, в котором при массе 1 кг изменение энтропии составляет 1 Дж/К.

Удельное количество теплоты q — величина, равная отношению количества теплоты dQ, подводимого к системе или отводимого от нее в ходе процесса, к массе dm системы:

dim q =L² T^-2, единица — джоуль на килограмм (J/kg; Дж/кг).

Джоуль на килограмм [9] равен удельному количествe теплоты процесса, в ходе которого к веществу массой 1 кг подводится (или отводится от него) количество теплоты 1 Дж.

Дата добавления: 2019-11-16; просмотров: 248; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!