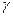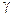Тема: «Использование формул полной вероятности и формулы Бейеса для нахождения вероятностей событий»
Цель: научиться применять теоремы сложения и умножения вероятностей для решения задач. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Пусть событие А может наступить при условии появления одного из несовместных событий B1, В2,..., Вn, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности Рв1(А), Рв2(А) , …, Рвn(А) события А. Как найти вероятность событияA? Ответ на этот вопрос дает следующая теорема.
Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий Bl, B2, ..., Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
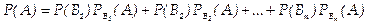
Эту формулу называют «формулой полной вероятности».
Пусть событие А может наступить при условии появления одного из несовместных событий B1, В2,..., Вn, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:
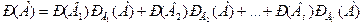
Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности
|
|
|
РА(В1), РА(В2),…, РА(Вn),
Условная вероятность любой гипотезы Ві (i = 1, 2, ..., n) может быть вычислена по формуле
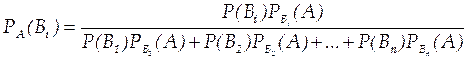
Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Решить задачи согласно своего варианта:
Вариант № 1
1. На сборку поступают детали с трёх автоматов. Первый даёт 25%, второй – 30% и третий – 30% и третий – 45% деталей данного типа, поступающих на сборку. Первый автомат допускает 0,1% нестандартных деталей, второй – 0,2%, третий – 0,3%. Найти вероятность поступления на сборку нестандартной детали.
2. В специализированную больницу поступает в среднем 60% больных с заболеванием К, 30% бальных с заболеванием Л, 10% с заболеванием М. Вероятность полного излечения болезни К равна 0,7, для болезней Л и М эти вероятности равны 0,8 и 0,9. Найти вероятность того, что наугад выбранный больной, поступивший в больницу, будет выписан здоровым.
|
|
|
3. Пусть в условиях предыдущей задачи больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.
Вариант № 2
1. Имеются два набора деталей. Вероятность того, что деталь первого набора бракована, равна 0,01%, а второго – 0,02. Найти вероятность того, что взятая наудачу деталь и наудачу взятого набора качественная.
2. Для сигнализации о том, что режим работы автоматической линии отклоняется от нормального, используется индикатор. Он принадлежит с вероятностями 0,2, 0,3 и 0,5 к одному из трёх типов, для которых вероятность срабатывания при нарушении нормальной работы равны соответственно 0,9, 0,7 и 0,6. Найти вероятность того, что наудачу взятый индикатор сработает при нарушении нормальной работы линии.
3. Пусть в условиях предыдущей задачи от индикатора получим сигнал. Найти вероятность того, что индикатор принадлежит к первому типу.
Вариант № 3
1. Имеются три урны с шарами. В первой урне 4 белых и 3 черных, во второй 5 белых и 2 черных, в третьей 2 белых и 5 черных. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар окажется белым.
2. На двух автоматических станках изготовляются одинаковые детали. Известно, что вероятность изготовления детали высшего качества на первом станке равна 0,92, а на втором – 0,8. Изготовленные на обоих станках не рассортированные детали находятся на складе. Среди них деталей, изготовленных на первом станке, в три раза больше, чем на втором. Найти вероятность того, что наудачу взятая деталь будет высшего качества.
|
|
|
3. Пусть в условиях предыдущей задачи наудачу взятая деталь окажется высшего качества. Найти вероятность того, что она изготовлена на втором станке.
Вариант № 4
1. Некоторое изделие может поступить для обработки в случайном порядке на один из трёх станков с вероятностями соответственно равными Р1=0,2; Р2=0,3; Р3=0,5. При обработке на первом станке вероятность брака равна 0,02, на втором – 0,3, на третьем - 0,05. Найти вероятность того, что поступившие в цех изделие после обработки окажется удовлетворяющим техническим условиям.
2. Пусть в условиях предыдущей задачи, поступившее в цех изделие после обработки оказалось удовлетворяющим техническим условиям. Какова вероятность того, что изделие обрабатывалось на третьем станке?
3. В ящике имеются 5 деталей, среди которых могут быть и бракованные. Вынутая наугад оказалось не бракованной. Найти вероятность того, что 3 детали в ящике не бракованные, а 2 бракованные, если предположить, что до опыта все гипотезы равновозможные.
|
|
|
Вариант № 5
1. Радиолампа может принадлежать к одной из двух партий с вероятностями р1=0,6 и р2=0,4. Вероятности того, что лампа проработает заданное число часов, равны для этих партий соответственно 0,7 и 0,8. Определить вероятность того, что лампа проработает заданное число часов.
2. Пусть в условиях предыдущей задачи лампа проработает заданное число часов. Какова вероятность того, что она принадлежит к первой партии?
3. В ящике имеются 4 детали, среди которых могут быть и бракованные. Вынутая наугад деталь оказалась не бракованной. Определить вероятность того, что все детали в ящике не бракованные. (Предполагается, что до опыта все гипотезы равновозможны).
Вариант № 6
1. В первой коробке 20 деталей, из них 18 стандартных, во второй коробке 10 деталей, из них 7 стандартных. Из второй коробки наудачу взята деталь и переложена в первую. Найти вероятность того, что деталь, наудачу извлеченная из первой коробки, стандартна.
2. Пусть в условиях предыдущей задачи деталь, извлеченная из первой коробки, оказалась стандартной. Найти вероятность того, что из второй коробки переложена в первую стандартная деталь.
3. Детали, изготовленные цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Найти вероятность того, что годная деталь будет признана стандартной.
Вариант № 7
1. Имеются два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. найти вероятность того, что взятая наудачу деталь из наудачу взятого набора нестандартна.
2. Пусть в условиях предыдущей задачи взятая наудачу деталь из наудачу взятого набора оказалась нестандартной. Какова вероятность того, что она принадлежала первому набору?
3. На сборку поступают детали с трех автоматов. Первый дает 20%, второй 30% и третий 50% деталей данного типа, поступающих на сборку. Первый автомат допускает 0,2% брака деталей, второй – 0,3%, третий – 0,5%. Найти вероятность того, что взятая наудачу деталь стандартна.
Вариант № 8
1. В цехе три типа автоматических станков производят одни и те же детали. Станки первого типа производят 0,94 деталей отличного качества, второго – 0,9 и третьего – 0,85. Все произведенные в цехе за смену детали в не рассортированном виде сложены на складе. Определить вероятность того, что взятая наудачу деталь окажется отличного качества, если станков первого типа 5 штук, второго – 3 штуки, третьего – 2 штуки и производительность всех одинакова.
2. Пусть в условиях предыдущей задачи взятая наудачу деталь оказалась отличного качества. Найти вероятность того, что она была произведена на станке первого типа.
3. Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором – 10 белых и 10 черных, в третьем – 20 черных шаров. Из выбранного наудачу ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.
Вариант № 9
1. В ящик, содержащий две детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.
2. Пусть в условиях предыдущей задачи извлечена стандартная деталь. Найти вероятность того, что первоначально в ящике была одна стандартная и одна нестандартная деталь.
3. По линии связи передаются два сигнала А и В соответственно с вероятностями 0,84 и 0,16. Из-за помех 1/6 часть сигналов А искажается и принимается как В-сигналы, а 1/8 часть переданных В-сигналов принимается как А–сигналы. Найти вероятность того, что на приемном пункте появится А –сигнал.
Вариант № 10
1. В группе спортсменов 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0,9, для велосипедистов – 0,8 и для бегуна – 0,6. найти вероятность того, что спортсмен, выбранный наудачу, выполнит квалификационную норму.
2. Пусть в условиях предыдущей задачи спортсмен выполнил квалификационную норму. Найти вероятность того, что это был велосипедист.
3. В двух урнах находятся белые и черные шары. В первой 3 белых и 2 черных, во второй 2 белых и 2 черных. Из первой урны наудачу вынимают один шар и перекладывают во вторую, а затем из второй урны наудачу извлекают один шар. Найти вероятность того, что этот шар будет белым.
Вариант № 11
1.Для участия в студенческих отборных соревнованиях выделено из первой группы курса 4, из второй 6, из третьей 5 студентов. Вероятность того, что студенты первой, второй и третьей групп попадут в сборную института соответственно равна 0,9; 0,7; и 0,6. Найти вероятность того, что студент, выбранный на удачу, в итоге соревнований попадет в сборную.
2. Пусть в условиях предыдущей задачи наудачу выбранный студент в итоге соревнований попал в сборную. Найти вероятность того, что это был студент первой группы.
3. В первом ящике содержатся 12 ламп, из них одна нестандартная; во втором 10 ламп, из них также одна нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.
Вариант № 12
1. Возле бензоколонки, стоящей на шоссе, проезжает в среднем 80% грузовых и 20% легковых автомашин. Вероятность того, что будет заправляться грузовая машина, равна 0,05, для легковой эта вероятность равна 0,1. Найти вероятность того, что выбранная наудачу машина будет заправляться.
2. В телевизионном ателье имеется 4 кинескопа разных типов. Вероятность того, что кинескоп выдержит гарантийный срок службы, соответственно равна 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок.
3. Пусть в условиях предыдущей задачи выбранный наудачу кинескоп выдержал гарантийный срок службы. Найти вероятность того, что это был кинескоп 1-го типа.
Вариант № 13
1. В первой коробке содержится 15 деталей, из них 12 стандартных, во второй коробке 10 деталей, из них8 стандартных. Из первой коробки наудачу взята деталь и переложена во вторую. Найти вероятность того, что деталь, наудачу извлеченная из второй, коробки будет стандартной.
2. Некоторое изделие может поступить для обработки в случайном порядке, на один из трех станков с вероятностью соответственно равной 0,2; 0,3; и 0,5. При обработке на первом станке вероятность брака равна 0,02, на втором станке-0,03 и на третьем-0,05. Найти вероятность того, что выбранное на удачу изделие после обработки оказалось бракованным.
3. Пусть в условиях предыдущей задачи поступившее в цех изделие после обработки оказалось доброкачественным.
Вариант № 14
1. Имеются два набора деталей. Вероятность того, что деталь первого набора бракованная, равна 0,01, а второго-0,02. Найти вероятность того, что взята наудачу деталь из наудачу взятого набора доброкачественная.
2. Радиолампа, поставленная в телевизор, может принадлежать к одной из трех партий с вероятностью 0,2; 0,5 и 0,3. Вероятность того, что лампа проработает определенное количество часов, для этих партий равна, соответственно 0,8; 0,6 и 0,9. Найти вероятность того, что выбранная наудачу лампа проработает определенное количество часов.
3. Пусть в условиях предыдущей задачи радиолампа, выбранная на удачу, проработала определенное число часов. Найти вероятность того, что радиолампа принадлежала первой партии.
Вариант № 15
1. В первом ящике содержатся 20 деталей, из них 15 стандартных, во втором-30 деталей, из них 27 стандартных; в третьем – 10 деталей, из них 9 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика стандартная.
2. Пусть в условиях предыдущей задачи наудачу извлеченная деталь оказалась нестандартной. Какова вероятность того, что она извлечена из первого ящика?
3. Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0,06, а на втором – 0,03. производительность первого автомата вдвое больше второго. Найти вероятность того, что наудачу взятая с конвейера деталь нестандартна.
Вариант № 16
1. Сборщик получил три коробки Деталей, изготовленных заводом № 1, две коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 0,9. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
2. Пусть в условиях предыдущей задачи сборщик извлек стандартную деталь. Какова вероятность того, что она изготовлена заводом № 1?
3. Для участия в студенческих отборочных соревнованиях выделено из первой группы четыре студента, из второй – десять, из третей шесть студентов. Вероятность того, что отобранный студент из первой, второй, третей групп попадает в сборную института, равна соответственно 0,5, 0,4 и 0,3. Наудачу выбранный участник соревнования попал в сборную. Какова вероятность того, что он из первой группы?
Вариант № 17
1. В группе легкоатлетов 8 барьеристов, 12 бегунов на длинные дистанции и 10 прыгунов с шестом. Вероятность выполнить квалификационную норму для барьериста равна 0,9, для бегуна – 0,5 и для прыгуна с шестом 0,6. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит квалификационную норму.
2. Пусть в условиях предыдущей задачи выбранный наудачу спортсмен выполнил квалификационную норму. Найти вероятность того, что это прыгун с шестом.
3. Среди поступающих на сборку деталей с первого станка 0,1% бракованных, со второго – 0,2%, с третьего - 0,3% и с четвертого – 0,5%. Производительности их относятся как 4:3:2:1 соответственно. Взятая наудачу деталь оказалась стандартной. Найти вероятность того, что она произведена на первом станке.
Вариант № 18
1. Имеется три набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,9, второго – 0,75, третьего – 0,6. Найти вероятность того, что взятая наудачу деталь из наудачу взятого набора стандартна.
2. Имеются две урны с шарами. В первой урне 34 белых и 6 черных, во второй 3 белых и 2 черных. Из первой урны наудачу извлекается один шар и перекладывается во вторую. Затем из второй урны извлекается шар. Найти вероятность того, что этот шар белый.
3. Пусть в условии предыдущей задачи из второй урны извлечен белый шар. Какова вероятность того, что из первой урны во вторую был переложен белый шар?
Вариант № 19
1. Пластмассовые болванки изготовляются на трех прессах. Первый пресс производит 50% всех болванок, второй – 30% и третий – 20%. При этом из болванок с первого пресса в среднем 0,03 нестандартных, из болванок со второго пресса с среднем 0,02 нестандартных, и из болванок с третьего пресса – 0,01 нестандартных. Какова вероятность того, что взятая наудачу болванка соответствует стандарту?
2. Пусть в условиях предыдущей задачи взятая наудачу болванка оказалась стандартной. Какова вероятность того, что она изготовлена на первом прессе?
3. В первой коробке содержатся 20 радиоламп, из них 18 стандартных; во второй коробке – 10 радиоламп, из них 8 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.
Вариант № 20
1. Детали для сборки изготавливаются на двух станках, из которых первый производит деталей в 4 раза больше второго. При этом брак составляет в выпуске первого станка 0,2, а в выпуске второго – 0,01. Найти вероятность того, что взятая наугад деталь окажется годной для сборки.
2. Пусть в условия предыдущей задачи взятая наугад деталь оказалась годной для сборки. Найти вероятность того, что она изготовлена на первом станке.
3. В первой урне находятся 2 белых и 3 черных шара, во второй – 4 белых и 1 черный. Из первой урны на удачу извлечен один шар и переложен во вторую. Найти вероятность того, что шар, наудачу извлеченный из второй урны, будет белый.
Вариант № 21
1. Некоторое изделие может поступить для обработки, в случайном порядке, на один из двух станков с вероятностями 0,6 и 0,4. При обработке на первом станке вероятность брака равна 0,02, на втором станке – 0,03. Найти вероятность того, что поступившее в цех изделие после обработки окажется удовлетворяющим техническим условиям.
2. Пусть в условиях предыдущей задачи поступившее в цех изделие после обработки оказалось удовлетворяющим техническим условиям. Найти вероятность того, что оно обрабатывалось на втором станке.
3. В двух урнах находятся шары белого и чёрного цвета. В первой урне – 5 белых и 3 чёрных, во второй – 3 белых и 2 чёрных. Из первой урны наудачу извлечён один шар и переложен во вторую. Найти вероятность того, что шар, наудачу извлечённый из второй урны, будет белого цвета.
Вариант № 22
1. Имеются два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,95, а второго – 0,85. Найти вероятность того, что взятая наудачу деталь из наудачу взятого набора стандартна.
2. Пусть в условиях предыдущей задачи извлечена нестандартная деталь. Найти вероятность того, что она извлечена из первого набора.
3. Имеются 5 винтовок, из которых две с оптическим прицелом. Вероятность попадания в цель при выстреле из винтовки с оптическим прицелом составляет для данного стрелка 0,95, без оптического прицела 0,8. Найти вероятность попадания в цель, если стрелок сделает один выстрел из наудачу взятой винтовки.
Вариант № 23
1. Прибор может работать в двух режимах: нормальном и ненормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, ненормальный – в 20%. Вероятность выхода из строя прибора за время Т в нормальном режиме равна 0,1, в ненормальном – 0,7. Найти вероятность выхода прибора из строя за время Т.
2. Пусть в условиях предыдущей задачи прибор вышел из строя за время Т. Найти вероятность того, что он работал в нормальном режиме
3. Имеются три одинаковые урны. В первой 5 белых и 3 черных, во второй 3 белых и 1 черный, в третьей только белые шары. Некто подходит наугад к одной из урн и вынимает из нее один шар. Найти вероятность того, что этот шар белый.
Вариант № 24
1. Приборы одного наименования изготовляются двумя заводами; первый завод поставляет 60 % всех изделий, второй – 40%. Вероятность безотказной работы за время Т прибора, изготовленного первым заводом, равна 0,9, вторым – 0,8. Определить вероятность безотказной работы взятого наудачу прибора, поступившего на производство
2. Пусть в условиях предыдущей задачи взятый наудачу прибор проработал безотказно время Т. Какова вероятность того, что этот прибор изготовлен первым заводом?
3. Пассажир может обратиться за получением билета в одну из двух касс. Вероятность обращения в каждую кассу зависит от их местоположения и равна соответственно 0,7 и 0,3. Вероятность того, что к моменту прихода пассажира билеты будут распроданы, равна для первой кассы 0,8, для второй – 0,4. Найти вероятность того, что, выбрав наудачу кассу, пассажир приобретает билет.
Вариант № 25
1. Производится стрельба по цели. Цель состоит из трех частей, площади которых равны S1, S2, S3 (S1 + S2+ S3 =S). Для попавшего в цель снаряда вероятность попасть в ту или другую часть пропорциональна площади части. При попадании в первую часть цель поражается с вероятностью Р1, во вторую – Р2, в третью – Р3. Найти вероятность поражения цели, если известно, что в нее попал один снаряд.
2. На первом заводе на каждые 100 лампочек производится в среднем 90 стандартных, на второми – 95, на третьем – 85, а продукция их составляет соответственно 50, 30 и 20 процентов всех электролампочек, поставляемых в магазтны данного района. Найти вероятность приобретения стандартной электролампочки.
3. Пусть в условиях предыдущей задачи элекролампочка, приобретенная в магазине данного района, оказалась стандартной. Найти вероятность того, что лампочка проиведена на первом заводе.
Контрольные вопросы
1. Каковы условия задачи, определяемой формулой полной вероятности?
2. Напишите формулу полной вероятности
3. Каковы условия задачи, определяемой формулой Бейеса?
4. Напишите формулу Бейеса.
Практическая работа № 5
Тема: «Использование формулы Бернулли. Локальная и интегральная теоремы Лапласа»
Цель: научиться применять формулы Бернулли, локальную и интегральную теоремы Лапласа. Научиться использовать справочные таблицы при решении задач. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Формула Бернулли. Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит п—k раз, по теореме умножения вероятностей независимых событий равна pkqn-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из п элементов по k элементов, т. е. Скп. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в п испытаниях) равна вероятности одного сложного события, умноженной на их число:
Полученную формулу называют формулой Бернулли.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции
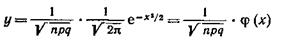
при 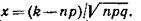
Имеются таблицы (приложение 1), в которых помещены значения функции 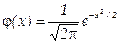 , соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция φ(х) четна, т. е. φ (—х) = φ(х).
, соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция φ(х) четна, т. е. φ (—х) = φ(х).
Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна
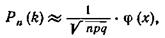
где 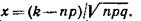
Теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп (k1, k2) того, что событие А появится в п испытаниях от k1 до k2 раз, приближенно равна определенному интегралу
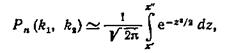
где 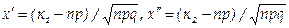
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл 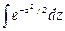 не выражается через элементарные функции. Таблица для интеграла
не выражается через элементарные функции. Таблица для интеграла 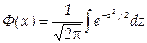 приведена в приложении 2. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х<0 пользуются той же таблицей [функция Ф(х) нечетна, т.е. Ф(—х) = —Ф(х)]. В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5. Функцию Ф(х) часто называют функцией Лапласа.
приведена в приложении 2. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х<0 пользуются той же таблицей [функция Ф(х) нечетна, т.е. Ф(—х) = —Ф(х)]. В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5. Функцию Ф(х) часто называют функцией Лапласа.
Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразовывают соотношение
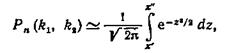
Итак, вероятность того, что событие А появится в п независимых испытаниях от k1 до k2 раз,
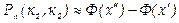
где 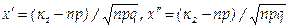
Решить задачи согласно своего варианта:
Вариант № 1
1. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленный нормы, равна 0,8. Найти вероятность того, что в ближайшие 5 суток расход электроэнергии в течение 3 суток не превысит нормы, а в остальные 2 суток превысит норму.
2. Вероятность обрыва нити на одно веретено в течение часа равна 0,1. Найти вероятность того, что число обрывов в час на 100 веретён будет:
а) ровно 16; б) не менее 7, но не более 13.
Вариант № 2
1. Найти вероятность того, что событие А появится в четырёх независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,2.
2. Вероятность поражения мишени при одном выстреле равна 0,9. Определить вероятность того, что при 100 выстрелах мишень будет поражена:
а) ровно 90 раз; б) от 81 до 93 раз.
Вариант № 3
1. В цеху 4 мотора. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,6. Найти вероятность того, что в данный момент:
а) включено два мотора;
б) включены все моторы;
2. Вероятность попадания по движущейся мишени равна 0,2. Какова вероятность того, что из 26 выстрелов:
а) 9 окажутся удачными;
б) число удачных выстрелов будет от 3 до 9?
Вариант № 4
1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Определить вероятность того, что из трех взятых наудачу взятых деталей:
а) две окажутся стандартными;
б) стандартными окажутся все три;
2. Вероятность выхода из строя за некоторое время Т одного конденсатора равна 0,1. Найти вероятность того, что из 100 конденсаторов в течение времени Т из строя выйдут:
а) ровно 16 конденсаторов;
б) от 4 до 19 конденсаторов;
Вариант № 5
1. В хлопке изменяется 10% коротких волокон. Какова вероятность того, что в наудачу взятом пучке из 4 волокон окажется не более двух коротких?
2. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что из 400 выстрелов мишень будет поражена:
а) ровно 300 раз
б) от 240 до 349 раз
Вариант № 6
1. Найти вероятность того, что событие А появятся в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность его появления равна 0,2.
2. Найти вероятность того, что среди наудачу взятых 100 деталей 55 окажутся отполированными, если в общей массе деталей имеются поровну отполированных и не отполированных. Какова вероятность того, что число отполированных деталей будет не менее 45 и не более 50?
Вариант № 7
1. Найти вероятность того, что в 5 независимых испытаниях событие А появятся хотя бы 3 раза, если в каждом из них вероятность его появления равна 0,1.
2. Производятся 400 независимых испытаний, в каждом из которых вероятность наступления события равна 0,5. Найти вероятность того, что события наступят:
а) ровно 220 раз;
б) от 220 до 240 раз
Вариант № 8
1. Всхожесть семян данного сорта растений оценивается вероятностью 0,3. Каковоа вероятность того, что из 5 посеянных семян взойдет не менее 4?
2. Вероятность появления события в каждом испытании равна 0,2. Производится 400 независимых испытаний. Определить вероятность того, что событие появится:
а) ровно 60 раз
б) не менее 70 и не более 100 раз.
Вариант № 9
1. Найти вероятность того, что событие А появится в четырёх независимых испытаниях не более двух раз, если в каждом испытании вероятность появления этого события равна 0,8.
2. Вероятность появления события А в одном испытании равна 0,6. Какова вероятность появления этого события не менее 342 и не более 378 раз, если произведено 600 независимых испытаний? Какова вероятность того, что событие наступит ровно 360 раз?
Вариант № 10
1. Монету бросают 5 раз. Найти вероятность того, что герб выпадет не менее 4 раз.
2. При массовом производстве диодов вероятность брака при формовке равна 0,1. Какова вероятность того, что из 400 наугад взятых диодов 50 будут бракованными? Найти вероятность того, что бракованных будет от 25 до 55 диодов.
Вариант № 11
1. Вероятность попадания в цель составляет при отдельном выстреле 0,8. Найти вероятность 2 попаданий при 6 выстрелах.
2. Делают 900 подбрасываний монеты. Найти вероятность того, что число появлений герба будет:
а) ровно 480;
б) от 420 до 480 раз;
Вариант № 12
1. По цели производится 5 выстрелов. Вероятность попадания в цель при одном выстреле равна 0,4. Для получения зачета по стрельбе требуется не менее 3 попаданий. Найти вероятность получения зачета.
2. В магазин поступило 400 книг по теории вероятности. Вероятность продажи каждой из них в течение дня равна 0,1. Найти вероятность того, что в течение дня будет продано:
а) ровно 40 книг;
б) от 30 до 50 книг.
Вариант № 13
1. Событие В появится в случае, если событие А появится не менее двух раз. Найти вероятность того, что наступит событие В, если будет произведено 5 независимых испытаний, и в каждом из которых вероятность появления события А равна 0,9.
2. При автоматической прессовке карболитных болванок 0,8 общего числа их не имеют зазубрин. Найти вероятность того, что из 100 взятых наудачу болванок число болванок без зазубрин будет:
а) ровно 75 штук;
б) не менее 75 и не более 85 штук.
Вариант № 14
1. В цехе 5 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включены 2 мотора.
2. При вытачивании болтов наблюдается в среднем 10% брака. Какова вероятность того, что в партии из 400 болтов пригодными окажутся:
а) ровно 360 штук
б) не менее 348 и не более 366 штук
Вариант № 15
1. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность двух попаданий при 5 выстрелах.
2. Электростанция обслуживает сеть с 10000 ламп. Вероятность включения каждой лампы равна 0,5. Определить вероятность того, что число одновременно включенных ламп будет:
а) ровно 5100
б) лежать в пределах между 4950 и 5050
Вариант № 16
1. Вероятность изготовления стандартной детали на автоматическом станке равна 0,9. Найти вероятность того, что из 5 взятых наудачу деталей, 2 окажутся стандартными.
2. Вероятность поражения мишени при одном выстреле равна 0,4. Найти вероятность того, что мишень будет поражена в серии из 600 выстрелов:
а) ровно 240 раз;
б) не менее 210 и не более 240 раз.
Вариант № 17
1. Монету бросают 6 раз. Найти вероятность того, что герб выпадет не менее двух раз.
2. Вероятность поражение мишени стрелком при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена:
а) ровно 90 раз;
б) не менее 75 и не более 85 раз.
Вариант № 18
1. Произведено 4 независимых испытания, в каждом из которых вероятность появления события А равна 0,7. Найти вероятность того, что событие А появится хотя бы 2 раза.
2. Штамповка металлических клемм для соединительных пластин дает 20% брака. Определить вероятность того, что из 400 клемм, выбранных на удачу, соответствующими стандарту будут:
а) ровно 300 штук;
б) не менее 310 не более 330 штук.
Вариант № 19
1. Рабочий обслуживает 4 станка. Каждый станок в течение 6 часов работы несколько раз останавливается и всего в сумме стоит 0,6 часа, причем остановки их в любой момент времени равновероятны. Определить вероятность того, что в данный момент времени будут работать 2 станка.
2. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется не проверенных:
а) ровно 80 деталей;
б) от 70 до 100 деталей.
Вариант № 20
1. В случайно выбранной семье 5 детей. Считая вероятность рождения мальчика и девочки одинаковой, определить вероятность того, что в выбранной семье окажутся три мальчика и две девочки.
2. Всхожесть хранящегося на складе зерна равна 80%. Отбираются случайным образом 100 зерен. Определить вероятность того, что среди них число всхожих зерен окажется:
а) от 68 до 90 штук;
б) ровно 80 штук.
Вариант № 21
1. На складе находятся 500 одинаковых коробок с обувью. Известно, что в 200 коробках обувь черного цвета и в 300 – коричневого. Коробки не рассортированы по цвету обуви. Служащий берет 5 первых попавшихся коробок. Определить вероятность того, что среди них окажутся 3 коробки с обувью черного и две коробки с обувью коричневого цвета.
2. Известно, что 0,8 всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Найти вероятность того, что среди 100 наудачу аппаратов первого сорта будут:
а) ровно 70 штук;
б) от 70 до 90 штук.
Вариант № 22
1. В семье 4 детей. Считая вероятность рождения мальчика и девочки одинаковой, найти вероятность того, что в этой семье 3 мальчика и 1 девочка.
2. Вероятность попадания в цель из скорострельного орудия равна при одном выстреле 0,9. Найти вероятность того, что при 100 выстрелах число попаданий будет:
а) ровно 93;
б) от 90 до 96.
Вариант № 23
1. В урне 30 белых и 20 черных шаров. Вынули подряд 3 шара, причем каждый вынутый шар возвращается в урну перед извлечением следующего и шары в урне перемешиваются. Какова вероятность того, что среди вынутых 3 шаров будет 1 белый.
2. При некотором технологическом процессе в среднем 1% шариков, изготовленных для подшипников, оказываются бракованными. Определить вероятность того, что среди поступивших на контроль 10000 шариков, бракованными окажутся:
а) 90 штук
б) от 80 до 100 штук
Вариант № 24
1. Вероятность появления события А равно 0,1. Какова вероятность того, что при 5 испытаниях событие А появится равно 3 раза?
2. По данным технического контроля в среднем 10% изготовляемых на заводе часов нуждаются в дополнительной регулировке. Чему равна вероятность того, что из 400 изготовленных часов будет нуждаться в дополнительной регулировке:
а) ровно 52 штуки;
б) от 34 до 52 штук?
Вариант № 25
1. Вероятность изготовления детали 1-го сорта на автоматическом станке равна 0,8. найти вероятность того, что из 3 взятых наудачу деталей 2 окажутся деталями 1-го сорта.
2. При данном технологическом процессе в среднем 90% всего числа изготовляемых заводом телефонных аппаратов являются продукцией высшей категории качества. Какова вероятность того, что из 100 выбранных наудачу телефонных аппаратов будут соответствовать продукции высшей категории качества:
а) ровно 84 аппарата;
б) от 84 до 96 аппаратов?
Контрольные вопросы
1. Объясните условие независимых испытаний
2. Запишите формулу Бернулли
3. Сформулируйте локальную предельную теорему Муавра-Лапласа
4. Сформулируйте интегральную предельную теорему Муавра-Лапласа
Практическая работа № 6
Тема: «Построение закона распределения вероятностей дискретных случайных величин. Нахождение числовых характеристик»
Цель: познакомится с понятием дискретной случайной величины, строить законы распределения вероятностей дискретной случайной величины. Научиться находить математическое ожидание, дисперсию и среднеквадратическое отклонение дискретной случайной величины. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично. Аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
| Х | х1 | х2 | … | хп |
| Р | р1 | р2 | … | рп |
События х1, х2, …, хп образуют полную группу, следовательно, сумма вероятностей этих событий равна единицы.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина X может принимать только значения х1, х2, ..., хп, вероятности которых соответственно равны р1, р2, .. ., рп. Тогда математическое ожидание М(X) случайной величины X определяется равенством
М(Х) = х1р1 + х2р2+...+хпрп.
Если дискретная случайная величина X принимает счетное множество возможных значений, то
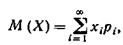
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = M[X—M(X)]2
Т.к. вычисления по этой формуле получаются громоздкими, то для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:
D(X) = M (X2) — [М (X)]2.
Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:
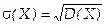
Решить задачи согласно своего варианта:
Вариант № 1
1. Вероятность попадания в цель при одном выстреле для данного стрелка равна 0,8. Стрелок производит 3 выстрела. Составить закон распределения случайной величины Х - числа попаданий в цель. Найти математическое ожидание и дисперсию случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,5, М(Х) = 3,5, D(X) = 0,25
Вариант № 2
1. Вероятность попадания в цель при одном выстреле для данного стрелка равна 0,9. Составить закон распределения случайной величины Х - число попаданий в цель при двух выстрелах. Найти математическое ожидание в дисперсию этой величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,5, М(Х) = 3, D(X) = 4
Вариант № 3
1. Игральная кость брошена 3 раза. Составить закон распределения случайной величины Х - числа появлений шестёрки. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,1, М(Х) = 1,9, D(X) = 0,09
Вариант № 4
1. Игральная кость брошена 2 раза. Составить закон распределения случайной величины Х - числа появлений 2. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,2, М(Х) = 2,6, D(X) = 0,64
Вариант № 5
1. Игральная кость брошена 4 раза. Составить закон распределения случайной величины Х - числа появления тройки. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,5, М(Х) = 5,5, D(X) = 0,25
Вариант № 6
1. Составить закон распределения вероятностей числа появлений события А в трех не зависимых испытаниях, если вероятность появления события в каждом испытании равна 0,6. Найти макс. ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,2, М(Х) = 1,8, D(X) = 0,16
Вариант № 7
1. Монета бросается 3 раза. Составить закон распределения случайной величины Х - числа появления герба. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,2, М(Х) = 2,8, D(X) = 0,16
Вариант № 8
1. Монета бросается 2 раза. Составить закон распределения случайной величины Х-числа появления герба. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,1, М(Х) = 2,8, D(X) = 0,36
Вариант № 9
1. Монета бросается 4 раза. Составить закон распределения случайной величины Х -числа появления герба. Найти математическое ожидание и дисперсию этой случайной величины
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,4, М(Х) = 2,2, D(X) = 1,96
Вариант № 10
1. Монета бросается 5 раз. Составить закон распределения случайной величины Х - числа появлений герба. Найти математическое ожидание и дисперсию этой величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,5, М(Х) = 2,5, D(X) = 2,25
Вариант № 11
1. Монета бросается 6 раз. Составить закон распределения случайной величины Х - числа появлений герба. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,9, М(Х) = 1,4, D(X) = 1,44
Вариант № 12
1. Производится 4 выстрела по мишени. Вероятность попаданий при каждом выстреле равна 0,8. Составить закон распределения случайной величины Х - числа попаданий в мишень. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,9, М(Х) = 1,1, D(X) = 0,09
Вариант № 13
1. По мишени ведутся выстрелы до первого попадания или до израсходования всех патронов. Составить закон распределения случайной величины Х - числа израсходованных патронов, если вероятность попадания при отдельном выстреле равна 0,8, а число имеющихся патронов 3. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,9, М(Х) = 1,2, D(X) = 0,36
Вариант № 14
1. По мишени ведутся выстрелы до первого попадания или до израсходования всех патронов. Составить закон распределения случайной величины Х - числа израсходованных патронов, если вероятность попадания при каждом выстреле 0,6, а число имеющихся патронов 4. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,9, М(Х) = 1,3, D(X) = 0,81
Вариант № 15
1. По мишени ведутся выстрелы до первого попадания или до израсходования всех патронов. Составить закон распределения случайной величины Х - числа израсходования патронов, если вероятность попадания при каждом выстреле 0,8, а число имеющихся патронов 5. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,8, М(Х) = 1,2, D(X) = 0,16
Вариант № 16
1. По мишени ведутся выстрелы до первого попадания или до израсходования всех патронов. Составить закон распределения случайной величины Х - числа израсходованных патронов, если вероятность попадания при каждом выстрелы 0,4, а число имеющихся патронов 5. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,8, М(Х) = 1,4, D(X) = 0,64
Вариант № 17
1. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,5. Составить закон распределения случайной величины Х - числа попадания в мишень при 5 выстрелах. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,8, М(Х) = 1,6, D(X) =1,44
Вариант № 18
1. Составить закон распределения случайной величины Х - числа появлений событий А в 2 независимых испытаниях, если вероятность появления событий в каждом испытании равна 0,3. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,8, М(Х) = 1,8, D(X) = 2,56
Вариант № 19
1. Составить закон распределения случайной величины Х - числа появлений событий А в трех независимых испытаниях, если вероятность появления события в каждом испытании равна 0,1. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,8, М(Х) = 2, D(X) = 4
Вариант № 20
1. Составить закон распределения случайной величины Х - числа появлений события А в четырех независимых испытаниях, если вероятность появления событий в каждом испытании равна 0,4. Найти математическое ожидание и дисперсию этой случайной
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,6, М(Х) = 1,4, D(X) = 0,25
Вариант № 21
1. В партии 10% нестандартных деталей. Наудачу отобраны три детали. Составить закон распределения случайной величины Х – числа стандартных деталей отобранных. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,6, М(Х) = 1,8, D(X) =1,96
Вариант № 22
1. В партии 10% нестандартных деталей. Наудачу отобраны 2 детали. Составить закон распределения случайной величины Х - числа нестандартных деталей среди двух отобранных. Найти математическое ожидание и дисперсию случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,6, М(Х) = 2,2, D(X) = 2,56
Вариант № 23
1. В партии из 8 деталей имеются 6 стандартных. Наудачу отобраны 2 детали. Составить закон распределения случайной величины Х - числа стандартных деталей среди двух отобранных. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,6, М(Х) = 2,6, D(X) =3,84
Вариант № 24
1. В партии из 8 деталей имеются 6 стандартных. Наудачу отобраны 3 детали. Составить закон распределения случайной величины Х - числа стандартных деталей среди трех отобранных. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,5, М(Х) = 1,5, D(X) = 0,25
Вариант № 25
1. В партии из 6 деталей имеются 4 стандартных. Наудачу отобраны 2 детали. Составить закон распределения случайной величины Х - числа стандартных деталей среди отобранных. Найти математическое ожидание и дисперсию этой случайной величины.
2. Дискретная случайная величина Х может принимать только 2 значения: Х1 и Х2, причем Х1<Х2. Известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х). Найти закон распределения этой случайной величины.
Р1 = 0,5, М(Х) = 2, D(X) = 1
Контрольные вопросы
1. Что называется случайной величиной? Примеры
2. Какую случайную величину называют дискретной? Пример
3. Какую случайную величину называют непрерывной? Пример
4. Что называют законом распределения дискретной случайной величины?
5. Что называют числовыми характеристиками случайной величины?
6. Что такое математическое ожидание?
7. Что характеризует математическое ожидание?
8. Свойства математического ожидания
9. Что является числовой характеристикой рассеяния случайной величины?
10. Формула для вычисления дисперсии
11. Свойства дисперсии
12. Что характеризует дисперсия?
13. Что называю среднеквадратическим отклонением случайной величины?
14. Как найти среднеквадратическое отклонение дискретной случайной величины?
Практическая работа № 7
Тема: «Определение функции и плотности распредления вероятностей случайной величины, построение графиков. Нахождение числовых характеристик»
Цель: Научиться находить функцию, плотность распределения вероятностей непрерывной случайной величины, строить графики функций, а также математическое ожидание, дисперсию и среднеквадратическое отклонение непрерывной случайной величины. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Пусть х—действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т. е. вероятность события X < х, обозначим через F(x). Разумеется, если х изменяется, то, вообще говоря, изменяется и F(x), т. е. F(x)—функция от х.
Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т. е.
F(x) = P(X < x).
Геометрически это равенство можно истолковать так: F (х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используют термин «интегральная функция».
График функции распределения расположен в полосе, ограниченной прямыми у = 0, у=1 (первое свойство).
При возрастании х в интервале (а, Ь), в котором заключены все возможные значения случайной величины, график «подымается вверх» (второе свойство).
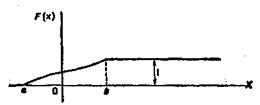
При х ≤ а ординаты графика равны нулю; при х ≥ b ординаты графика равны единице (третье свойство).
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) — первую производную от функции распределения F(x):
f(x) = F'(x).
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:
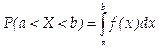
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f (х) и прямыми х = а и х = b.
Зная плотность распределения f(x), можно найти функцию распределения F (х) по формуле
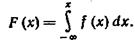
По известной функции распределения может быть найдена плотность распределения, а именно:
f(x) = F'(x).
Решить задачи согласно своего варианта:
Вариант № 1
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 2 | 3 | 6 |
| Р | 0,4 | 0,5 | 0,1 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 
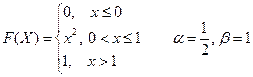
Вариант № 2
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 1 | 3 | 5 |
| Р | 0,6 | 0,1 | 0,3 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 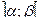
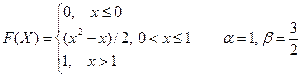
Вариант № 3
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 1 | 4 | 6 |
| Р | 0,2 | 0,4 | 0,4 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 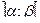
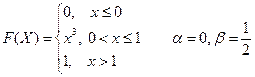
Вариант № 4
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 2 | 5 | 8 |
| Р | 0,4 | 0,5 | 0,1 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 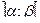
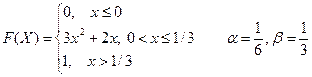
Вариант № 5
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 7 | 10 |
| Р | 0,1 | 0,5 | 0,4 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 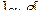
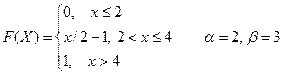
Вариант № 6
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 4 | 6 | 7 |
| Р | 0,2 | 0,3 | 0,5 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 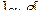
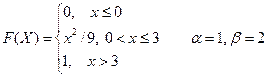
Вариант № 7
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 5 | 7 |
| Р | 0,4 | 0,5 | 0,1 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 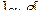
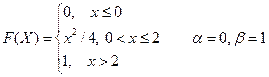
Вариант № 8
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 1 | 4 | 7 |
| Р | 0,3 | 0,5 | 0,2 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 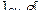
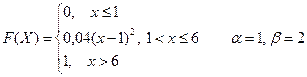
Вариант № 9
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 5 | 7 | 9 |
| Р | 0,1 | 0,5 | 0,4 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 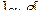

Вариант № 10
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 4 | 8 | 12 |
| Р | 0,3 | 0,5 | 0,2 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 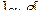
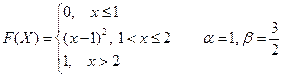
Вариант № 11
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 2 | 3 | 4 |
| Р | 0,7 | 0,1 | 0,2 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 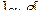
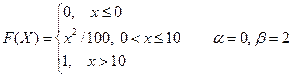
Вариант № 12
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 6 | 9 |
| Р | 0,5 | 0,3 | 0,2 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 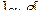
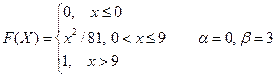
Вариант № 13
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 1 | 5 | 7 |
| Р | 0,2 | 0,2 | 0,6 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 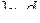
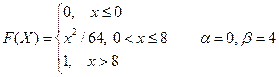
Вариант № 14
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 2 | 5 | 9 |
| Р | 0,2 | 0,7 | 0,1 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 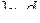
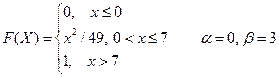
Вариант № 15
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 6 | 8 |
| Р | 0,4 | 0,3 | 0,3 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 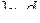
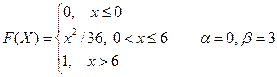
Вариант № 16
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 2 | 3 | 5 |
| Р | 0,1 | 0,7 | 0,2 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 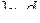
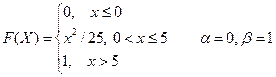
Вариант № 17
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 4 | 8 | 10 |
| Р | 0,1 | 0,2 | 0,7 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 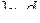
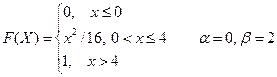
Вариант № 18
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 10 | 12 |
| Р | 0,2 | 0,1 | 0,7 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 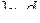
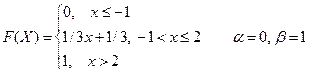
Вариант № 19
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 5 | 8 | 10 |
| Р | 0,8 | 0,1 | 0,1 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 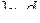
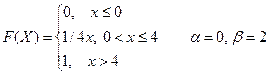
Вариант № 20
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 4 | 8 |
| Р | 0,6 | 0,1 | 0,3 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 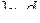
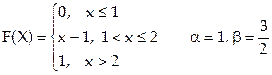
Вариант № 21
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 1 | 2 | 3 |
| Р | 0,5 | 0,2 | 0,3 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 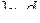
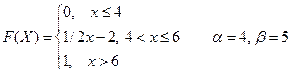
Вариант № 22
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 8 | 10 | 11 |
| Р | 0,3 | 0,3 | 0,4 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 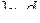
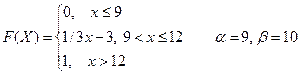
Вариант № 23
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 2 | 3 | 8 |
| Р | 0,1 | 0,3 | 0,6 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 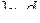
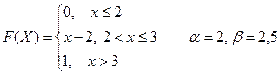
Вариант № 24
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 5 | 6 | 8 |
| Р | 0,2 | 0,7 | 0,1 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 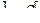
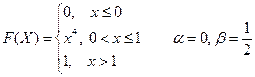
Вариант № 25
1. Дискретная случайная величина Х задана законом распределения. Найти функцию распределения F(X) и начертить ее график
| Х | 3 | 10 | 15 |
| Р | 0,1 | 0,1 | 0,8 |
2. Случайная величина Х задана функцией распределения F(X). Найти: а) плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины; б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу 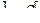
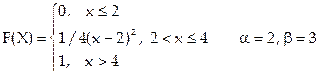
Контрольные вопросы
1. Определение функции распределения. Пример
2. Свойства функции распределения.
3. График функции распределения. Пример
4. Что называют плотностью распределения вероятностей непрерывной случайной величины?
5. Как найти вероятность попадания непрерывной случайной величины в заданный интервал?
6. Свойства плотности распределения
7. Что называют математическим ожиданием непрерывной случайной величины?
8. Что называют дисперсией непрерывной случайной величины?
9. Как найти среднеквадратическое отклонение непрерывной случайной величины?
Практическая работа № 8
Тема: «Нормальное распределение. Вычисление вероятнгостей заданного отклонения»
Цель: научиться находить параметры нормального распределения, вероятности попадания в заданный интервал нормальной случайной величины; находить верояности заданного отклонения; использовать правило трех сигм. Научиться использовать справочные таблицы при решении задач. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
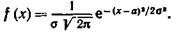
Мы видим, что нормальное распределение определяется двумя параметрами: а и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение.
Вероятностный смысл этих параметров таков: а есть математическое ожидание, σ — среднее квадратическое отклонение нормального распределения.
М (X) = а, т. е. математическое ожидание нормального распределения равно параметру а.
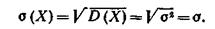
Среднее квадратическое отклонение нормального распределения равно параметру σ.
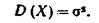
Уже известно, что если случайная величина X задана плотностью распределения f(х), то вероятность того, что X примет значение, принадлежащее интервалу (α, β), такова:
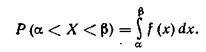
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (α, β), равна
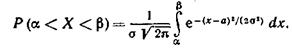
Пользуясь функцией Лапласа

окончательно получим
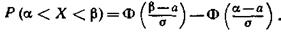
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа δ, т. е. требуется найти вероятность осуществления неравенства
|Х—а|< δ.
Заменим это неравенство равносильным ему двойным неравенством
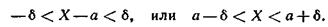
Пользуясь ранее полученной формулой, получим
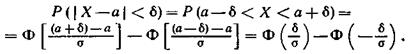
Приняв во внимание равенство
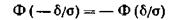
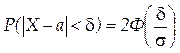
Преобразуем формулу
Р(|Х-а|< δ) = 2Ф(δ / σ) , положив δ = σ t. В итоге получим
Р(|Х— а|< σ t) = 2Ф(t).
Если t = 3 и, следовательно, σ t = Зσ, то
Р (| X — а |< Зσ) = 2Ф (3) = 2 ∙ 0,49865 = 0,9973,
т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Решить задачи согласно своего варианта:
Вариант № 1
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 13, σ = 7, a = 8, β = 11, δ = 2
2. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с параметрами а = 16км, σ = 100м. Найти вероятность того, что расстояние между этими пунктами не меньше 15,8км
Вариант № 2
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 12, σ = 3, a = 7, β = 13, δ = 5
2. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с параметрами а = 16км, σ = 100м. Найти вероятность того, что расстояние между этими пунктами не более 16,25км
Вариант № 3
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 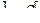
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 9, σ = 5, a = 3, β = 10, δ = 6
2. Рост взрослого мужчины является случайной величиной, распределенной по нормальному закону. Пусть ее математическое ожидание равно 170см, а дисперсия – 36. Вычислить вероятность того, что хотя бы один из наудачу выбранных четырех мужчин будет иметь рост от 168см до 172см
Вариант № 4
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 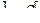
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 8, σ = 9, a = 10, β = 16, δ = 10
2. Рост взрослой женщины является случайной величиной, распределенной по нормальному закону с параметрами а = 164см, σ = 5,5см. Вычислить вероятность того, что одна из наудачу выбранных трех женщин имеет рост от 153см до 175см
Вариант № 5
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 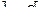
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 14, σ = 8, a = 4, β = 18, δ = 8
2. Диаметр детали, изготовленной заводом, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001, а математическое ожидание – 2,5см. Найти границы, в которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали.
Вариант № 6
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 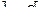
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 3, σ = 10, a = 5, β = 12, δ = 16
2. Производится измерение диаметра вала без систематических ошибок, случайные ошибки измерения Х подчинены нормальному закону со средним квадратическим отклонением σ = 5мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 7мм
Вариант № 7
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 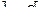
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 7, σ = 10, a = 14, β = 19, δ = 12
2. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки подчинены нормальному закону со средним квадратическим отклонением σ = 10г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 5г.
Вариант № 8
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 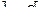
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 5, σ = 6, a = 12, β = 16, δ = 12
2. Автомат штампует детали. Деталь считается годной, если отклонение Х ее длины от проектной не превышает 0,9мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением σ = 0,5мм, найти сколько в среднем будет годных деталей среди 100 изготовленных
Вариант № 9
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 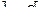
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 4, σ = 11, a = 16, β = 23, δ = 24
2. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 12мм. Случайные отклонения размера от проектного подчинены нормальному закону со средним квадратическим отклонением σ =8мм. Какова вероятность изготовления годной детали автоматом?
Вариант № 10
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 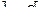
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 6, σ = 13, a = 15, β = 26, δ = 8
2. Случайная величина Х распределена нормально с математическим ожиданием а=20 и средним квадратическим отклонением σ = 5. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9544 попадет величина Х в результате испытания.
Вариант № 11
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 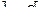
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 10, σ = 4, a = 2, β = 13, δ = 6
2. Случайная величина Х распределена нормально со средним квадратическим отклонением σ =10 мм. Найти длину интервала, симметричного относительно математического ожидания, в которой с вероятностью 0,6826 попадёт Х в результате испытания.
Вариант № 12
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 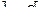
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 9, σ = 5, a = 5, β = 14, δ = 6
2. Станок-автомат изготовляет шарики, причём контролируется их диаметр Х. Считая, что Х – нормально распределённая случайная величина с математическим ожиданием a=6 мм и средним квадратическим отклонением σ =0,1 мм, найти интервал, симметричный относительно математического ожидания, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных шариков.
Вариант № 13
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 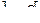
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 8, σ = 2, a = 4, β = 9, δ = 3
2. Размер диаметра детали, выпускаемой цехом, распределяется по нормальному закону с параметрами а=5 мм, σ 2=0,81. Найти вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более, чем на 2см.
Вариант № 14
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 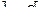
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 7, σ = 2, a = 3, β = 10, δ = 1
2. Результаты измерения расстояния между двумя населёнными пунктами подчинены нормальному закону с параметрами а=200 км, σ =500 м. Найти вероятность того, что расстояние между этими пунктами не меньше 199км.
Вариант № 15
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 6, σ = 3, a = 2, β = 11, δ = 5
2. Результаты измерения расстояния между двумя населёнными пунктами подчинены нормальному закону с параметрами а=100 км, σ =200 м. Найти вероятность того, что расстояние между этими пунктами не более 100,4км.
Вариант № 16
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 5, σ = 4, a = 2, β = 12, δ = 3
2. Рост взрослого мужчины является случайной величиной, распределённой по нормальному закону с параметрами а=174 см, σ =6 см. Вычислить вероятность того, что хотя бы один из наудачу выбранных мужчин будет иметь рост от 168 до 180см.
Вариант № 17
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 4, σ = 5, a = 2, β = 11, δ = 7
2. Рост взрослого мужчины является случайной величиной, распределённой по нормальному закону. Пусть её математическое ожидание равно 174см, а дисперсия – 64. Вычислить вероятность того, что один из двух наудачу выбранных мужчин будет иметь рост от 170 см до 178 см.
Вариант № 18
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 3, σ = 2, a = 3, β = 6, δ = 3
2. Длина некоторой детали, изготовленной заводом, является случайной величиной, распределённой по нормальному закону. Математическое ожидание её равно 20 см, а дисперсия – 0,01. Найти интервал, в котором с вероятностью 0,9973 заключена длина наудачу взятой детали.
Вариант № 19
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 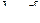
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 2, σ = 5, a = 4, β = 9, δ = 9
2. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением σ =50 мг. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящих по абсолютной величине 10 мг.
Вариант № 20
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 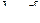
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 2, σ = 4, a = 6, β = 10, δ = 5
2. Вес карпа, вылавливаемого из колхозного пруда, подчинён нормальному закону с параметрами а=1200г и σ =50г. Найти вероятность того, что вес первого карпа, пойманного на удочку в этом пруду, не будет превышать 1250г.
Вариант № 21
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 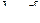
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 15, σ = 2, a = 12, β = 19, δ = 3
2. Вес клубней картофеля, подготовленного для посадки, подчинён нормальному закону с параметрами а=60г, σ =5г. Найти вероятность того, что вес наудачу взятого клубня будет не меньше 55г.
Вариант № 22
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 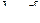
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 14, σ = 4, a = 10, β = 20, δ = 8
2. Случайная величина Х распределена нормально с параметрами а=45 и σ =2. Найти
интервал, симметричный относительно математического ожидания, который с вероятностью 0,4844 попадёт Х в результате испытания.
Вариант № 23
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 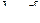
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 13, σ = 5, a = 11, β = 21, δ = 8
2. Случайная величина Х распределена нормально с математическим ожиданием а=24. Вероятность попадания Х в интервал ]24; 30[ равна 0,3. Чему равна вероятность попадания Х в интервал ]18; 30[ ?
Вариант № 24
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 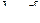
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 12, σ = 5, a = 12, β = 22, δ = 12
2. Стрельба ведётся из орудия вдоль некоторой прямой. Средняя дальность полёта снаряда равна 1200м. Предполагая, что дальность полёта Х распределена по нормальному закону со средним квадратическим отклонением 40м, найти, какой процент выпускаемых снарядов даст перелёт от 60 до 80м.
Вариант № 25
1. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины Х. Найти:
а) вероятность того, что в результате испытания случайная величина попадет в интервал 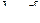
б) вероятность того, что абсолютная величина отклонения случайной величины от своего математического ожидания меньше положительного числа δ.
а = 11, σ = 8, a = 13, β = 23, δ = 6
2. На станке изготовляется некоторая деталь. Ее длина Х представляет собой случайную величину, распределенную по нормальному закону со средним значением 20см и средним квадратическим отклонением 0,2см. Какой процент деталей, изготовленных на этом станке, будет иметь длину, отличающуюся от средней не более чем на 0,3 см?
Контрольные вопросы
1. Что называют нормальным распределением?
2. Какими параметрами определяется нормальное распределение?
3. Чему равно математическое ожидание нормального распределения?
4. Чему равна дисперсия нормального распределения?
5. Чему равно среднеквадратическое отклонение нормального распределения?
6. Какой график имеет нормальная кривая?
7. Как вычислить попадание в заданный интервал нормальной случайной величины?
8. Как вычислить вероятность заданного отклонения?
9. Как используется правило трех сигм?
Практическая работа № 9
Тема: «Расчет сводных характеристик выборки»
Цель: научиться пользоваться методом произведений для вычисления выборочных средней и дисперсии. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h. Условными называют варианты, определяемые равенством
ui = (xi – C)/h
где С – ложный нуль (новое начало отсчета), h – шаг, т.е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба)
Обычным эмпирическим моментом порядка k называют среднее значение k-x степеней разностей хi—С:
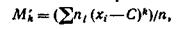
где xi—наблюдаемая варианта, ni—частота варианты, 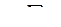 - объем выборки, С—произвольное постоянное число (ложный нуль).
- объем выборки, С—произвольное постоянное число (ложный нуль).
Начальным эмпирическим моментом порядка k называют обычный момент порядка k при С — О
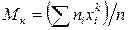
Центральным эмпирическим моментом порядка k называют обычный момент порядка k при 
В частности,
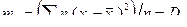
т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.
Условным эмпирическим моментом порядка k называют начальный момент порядка k, вычисленный для условных вариант:
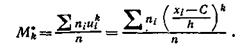 I
I
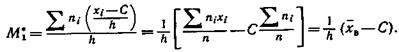
Отсюда
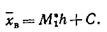
Формула для вычисления выборочной дисперсии по условным моментам первого и второго порядков
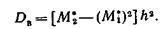
Решить задачи согласно своего варианта:
Вариант № 1
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 5,2 | 5,6 | 6,0 | 6,4 | 6,8 | 7,2 | 7,6 | 8,0 | 8,4 | 8,8 | 9,2 | 6,6 |
| частоты | 8 | 7 | 4 | 10 | 25 | 57 | 9 | 11 | 4 | 5 | 3 | 7 |
Вариант № 2
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 1,25 | 3,25 | 5,25 | 7,25 | 9,25 | 11,25 | 13,25 | 15,25 | 17,25 | 19,25 | 21,25 |
| частоты | 32 | 40 | 90 | 110 | 74 | 144 | 10 | 1 | 3 | 7 | 5 |
Вариант № 3
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 10,3 | 10,5 | 10,7 | 10,9 | 11,1 | 11,3 | 11,5 | 11,7 | 11,9 | 12,1 | 12,3 | 12,5 |
| частоты | 4 | 7 | 8 | 10 | 25 | 15 | 12 | 10 | 4 | 5 | 6 | 4 |
Вариант № 4
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 |
| частоты | 12 | 40 | 90 | 120 | 88 | 400 | 10 | 2 | 7 | 5 | 4 |
Вариант № 5
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 | 10,5 | 11,5 | 12,5 | 13,5 |
| частоты | 75 | 175 | 300 | 75 | 130 | 405 | 200 | 5 | 7 | 6 | 9 |
Вариант № 6
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 |
| частоты | 15 | 47 | 6 | 48 | 14 | 350 | 1 | 47 | 63 | 52 | 22 |
Вариант № 7
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 3,15 | 4,15 | 5,15 | 6,15 | 7,15 | 8,15 | 9,15 | 10,15 | 11,15 | 12,15 | 13,15 |
| частоты | 75 | 175 | 30 | 75 | 130 | 405 | 100 | 2 | 7 | 3 | 57 |
Вариант № 8
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 1,15 | 3,15 | 5,15 | 7,15 | 9,15 | 11,15 | 13,15 | 15,15 | 17,15 | 19,15 | 21,15 |
| частоты | 38 | 2 | 198 | 56 | 6 | 250 | 50 | 2 | 13 | 5 | 48 |
Вариант № 9
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 | 10,5 | 11,5 | 12,5 | 13,5 |
| частоты | 65 | 165 | 290 | 85 | 130 | 345 | 220 | 10 | 14 | 2 | 5 |
Вариант № 10
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 2,25 | 2,75 | 3,25 | 3,75 | 4,25 | 4,75 | 5,25 | 5,75 | 6,25 | 6,75 | 7,25 |
| частоты | 7 | 13 | 13 | 12 | 5 | 60 | 30 | 2 | 4 | 45 | 8 |
Вариант № 11
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 325 | 375 | 425 | 475 | 525 | 575 | 625 | 675 | 725 | 775 | 825 |
| частоты | 3 | 12 | 25 | 28 | 12 | 520 | 2 | 4 | 7 | 1 | 9 |
Вариант № 12
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
| частоты | 27 | 68 | 47 | 29 | 9 | 120 | 7 | 8 | 9 | 4 | 2 |
Вариант № 13
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 2,25 | 2,75 | 3,25 | 3,75 | 4,25 | 4,75 | 5,25 | 5,75 | 6,25 | 6,75 | 7,25 |
| частоты | 13 | 22 | 59 | 20 | 6 | 72 | 18 | 5 | 47 | 8 | 9 |
Вариант № 14
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 |
| частоты | 10 | 20 | 20 | 16 | 16 | 88 | 10 | 5 | 4 | 8 | 4 |
Вариант № 15
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 6,3 | 12,3 | 18,3 | 24,3 | 30,3 | 36,3 | 42,3 | 48,3 | 54,3 | 60,3 | 66,3 |
| частоты | 7 | 8 | 20 | 10 | 5 | 97 | 23 | 57 | 4 | 8 | 9 |
Вариант № 16
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 110 | 115 | 120 | 125 | 130 | 135 | 140 | 145 | 150 | 155 | 160 |
| частоты | 5 | 10 | 17 | 12 | 6 | 50 | 2 | 41 | 5 | 7 | 14 |
Вариант № 17
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
| частоты | 1 | 7 | 18 | 18 | 6 | 50 | 35 | 42 | 4 | 8 | 5 |
Вариант № 18
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,1 | 1,2 | 1,3 |
| частоты | 10 | 30 | 10 | 26 | 16 | 80 | 5 | 2 | 7 | 14 | 6 |
Вариант № 19
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 0,15 | 1,15 | 2,15 | 3,15 | 4,15 | 5,15 | 6,15 | 7,15 | 8,15 | 9,15 | 10,15 |
| частоты | 10 | 16 | 25 | 26 | 14 | 90 | 14 | 7 | 25 | 34 | 9 |
Вариант № 20
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| частоты | 3 | 10 | 13 | 12 | 92 | 40 | 20 | 13 | 47 | 5 | 8 |
Вариант № 21
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 154 | 158 | 162 | 166 | 170 | 174 | 178 | 182 | 186 | 190 | 194 |
| частоты | 10 | 14 | 26 | 22 | 12 | 72 | 4 | 8 | 2 | 4 | 15 |
Вариант № 22
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 |
| частоты | 45 | 40 | 10 | 30 | 10 | 225 | 270 | 180 | 90 | 24 | 7 |
Вариант № 23
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 28 | 31 | 34 | 37 | 40 | 43 | 46 | 49 | 52 | 55 | 58 |
| частоты | 5 | 13 | 22 | 28 | 18 | 310 | 4 | 14 | 7 | 23 | 2 |
Вариант № 24
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 4,5 | 10,5 | 16,5 | 22,5 | 28,5 | 34,5 | 40,5 | 46,5 | 52,5 | 58,5 | 64,5 |
| частоты | 30 | 110 | 240 | 310 | 215 | 395 | 14 | 4 | 75 | 2 | 4 |
Вариант № 25
Найти методом произведений выборочные среднее квадратическое отклонение и дисперсию по данному статистическому распределению выборки:
| Варианты | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 | 10,5 |
| частоты | 20 | 10 | 240 | 310 | 215 | 395 | 114 | 4 | 75 | 12 | 4 |
Контрольные вопросы
1. Какие варианты называют равноотстоящими?
2. Какие варианты называют условными?
3. Что называют обычным эмпирическим моментом?
4. Что называют начальным эмпирическим моментом?
5. Что называют центральным эмпирическим моментом?
6. Что называют условным эмпирическим моментом?
7. Как выражаются обычные моменты через условные?
8. Как выражаются центральные моменты через условные?
9. Техника вычислений центральных моментов по условным с помощью метода произведений.
Практическая работа № 10
Тема: «Вычисление параметров выборочного уравнения прямой линии регрессии по сгруппированным данным. Выборочный коэффициент корреляции»
Цель: научиться применять формулы Бернулли, локальную и интегральную теоремы Лапласа. Научиться использовать справочные таблицы при решении задач. Формировать приемы правильного оформления работы, рациональной записи решения. Обращать внимание на грамотность использования формул, правильный анализ условия задачи. Развивать продуктивное мышление и навыки самоконтроля.
Ход работы
Используя новую величину – выборочный коэффициент корреляции, получим уравнение регрессии в следующем виде
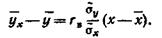
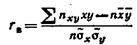 , или
, или 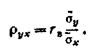
Аналогично, выборочное уравнение прямой линии регрессии X на Y вида
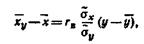
Выборочный коэффициент корреляции определяется равенством
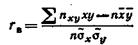
где х, у—варианты (наблюдавшиеся значения) признаков X и Y; nху — частота пары вариант (х, у); n — объем выборки (сумма всех частот);  ,
,  —выборочные средние квадратические отклонения;
—выборочные средние квадратические отклонения;  ,
, 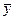 —выборочные средние.
—выборочные средние.
Известно, что если величины Y и X независимы, то коэффициент корреляции r =0; если r = ± 1, то Y и X связаны линейной функциональной зависимостью. Отсюда следует, что коэффициент корреляции r измеряет силу (тесноту) линейной связи между У и X.
Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии.
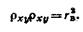
Отсюда
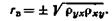
Знак при радикале совпадать со знаком коэффициентов регрессии.
Методика вычисления выборочного коэффициента корреляции
Пусть требуется по данным корреляционной таблицы вычислить выборочный коэффициент корреляции. Можно значительно упростить расчет, если перейти к условным вариантам (при этом величина rв не изменится)
ui=(xi – C1)/h1 и vi = (yj – C2)/h2
В этом случае выборочный коэффициент корреляции вычисляют по формуле
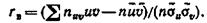
Величины 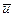 ,
, 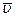 ,
,  ,
,  можно найти методом произведений, а при малом числе данных — непосредственно исходя из определений этих величин. Остается указать способ вычисления
можно найти методом произведений, а при малом числе данных — непосредственно исходя из определений этих величин. Остается указать способ вычисления 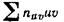 , где nuv — частота пары условных вариант (u, v).
, где nuv — частота пары условных вариант (u, v).
Можно доказать, что справедливы формулы:
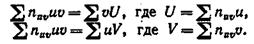
Для контроля целесообразно выполнить расчеты по обеим формулам и сравнить результаты; их совпадение свидетельствует о правильности вычислений.
Решить задачи согласно своего варианта:
Вариант № 1
Дана корреляционная таблица.
| У | Х | |||||||
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | nу | |
| 5 | 7 | 3 | - | - | - | - | - | 10 |
| 7 | 4 | 8 | 2 | - | - | - | - | 14 |
| 9 | - | 5 | 11 | 5 | - | - | - | 21 |
| 11 | 2 | 4 | 8 | 13 | 1 | 2 | - | 30 |
| 13 | 1 | - | - | 7 | 16 | 6 | 3 | 33 |
| 15 | - | - | 2 | 1 | 3 | 19 | 7 | 32 |
| 17 | - | - | - | - | - | 3 | 17 | 20 |
| nх | 14 | 20 | 23 | 26 | 20 | 30 | 27 | n = 160 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 2
Дана корреляционная таблица.
| У | Х | |||||||
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | nу | |
| 5 | - | - | - | - | - | 2 | 5 | 7 |
| 9 | - | - | - | 1 | 6 | 1 | - | 8 |
| 13 | - | - | 6 | 2 | 2 | - | - | 10 |
| 17 | - | 4 | 3 | 1 | - | - | - | 8 |
| 21 | 2 | 4 | 1 | - | - | - | - | 7 |
| 25 | 7 | 3 | - | - | - | - | - | 10 |
| nх | 9 | 11 | 10 | 4 | 8 | 3 | 5 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 3
Дана корреляционная таблица.
| У | Х | |||||||
| 15 | 25 | 35 | 45 | 55 | 65 | 75 | nу | |
| 9 | 2 | 4 | - | - | - | - | - | 6 |
| 15 | 5 | 6 | 1 | - | - | - | - | 12 |
| 21 | - | 3 | 8 | 12 | 2 | - | - | 25 |
| 27 | - | - | 9 | 16 | 6 | - | - | 31 |
| 33 | - | - | 3 | 2 | 4 | 7 | 1 | 17 |
| 39 | - | - | - | - | 1 | 2 | 6 | 9 |
| nх | 7 | 13 | 21 | 30 | 13 | 9 | 7 | n = 100 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 4
Дана корреляционная таблица.
| У | Х | |||||
| 5 | 15 | 25 | 35 | 45 | nу | |
| 0,5 | 7 | - | - | - | - | 7 |
| 5,5 | 11 | 5 | - | - | - | 16 |
| 10,5 | - | 19 | 15 | 5 | - | 39 |
| 15,5 | - | 3 | 15 | 6 | 1 | 25 |
| 20,5 | - | - | 2 | 4 | 4 | 10 |
| 25,5 | - | - | - | - | 3 | 3 |
| nх | 18 | 27 | 32 | 15 | 8 | n = 100 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 5
Дана корреляционная таблица.
| У | Х | |||||
| 10 | 15 | 20 | 25 | 30 | nу | |
| 2,5 | - | - | - | - | 6 | 6 |
| 3,0 | - | - | - | 6 | 6 | 12 |
| 3,5 | 2 | 4 | 2 | - | - | 8 |
| 4,0 | - | - | 6 | 4 | - | 10 |
| 4,5 | 4 | - | - | - | - | 4 |
| nх | 6 | 4 | 8 | 10 | 12 | n = 40 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 6
Дана корреляционная таблица.
| У | Х | |||||
| 325 | 375 | 425 | 475 | 525 | nу | |
| 125 | 3 | - | - | - | - | 3 |
| 175 | 2 | 8 | 2 | - | - | 12 |
| 225 | - | 7 | 5 | 13 | - | 25 |
| 275 | - | 1 | 10 | 10 | 7 | 28 |
| 325 | - | - | - | 7 | 5 | 12 |
| nх | 5 | 16 | 17 | 30 | 12 | n = 80 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 7
Дана корреляционная таблица.
| У | Х | |||||
| 100 | 200 | 300 | 400 | 500 | nу | |
| 7,75 | - | - | 1 | 2 | 1 | 4 |
| 8,25 | - | 3 | -10 | 1 | - | 14 |
| 8,75 | 3 | 40 | 2 | - | - | 45 |
| 9,25 | 5 | 20 | 1 | - | - | 26 |
| 9,75 | 10 | 1 | - | - | - | 11 |
| nх | 18 | 64 | 14 | 3 | 1 | n = 100 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 8
Дана корреляционная таблица.
| У | Х | |||||
| 15 | 25 | 35 | 45 | 55 | nу | |
| 25 | 7 | 20 | - | - | - | 27 |
| 35 | 5 | 23 | 30 | 10 | - | 68 |
| 45 | - | - | 47 | 11 | 9 | 67 |
| 55 | - | - | 2 | 20 | 7 | 29 |
| 65 | - | - | - | 6 | 3 | 9 |
| nх | 12 | 43 | 79 | 47 | 19 | n = 200 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 9
Дана корреляционная таблица.
| У | Х | |||||
| 500 | 1500 | 2500 | 3500 | 4500 | nу | |
| 1,75 | - | - | - | 1 | 6 | 7 |
| 2,25 | - | - | 4 | 6 | 3 | 13 |
| 2,75 | - | 3 | 6 | 4 | - | 13 |
| 3,25 | 2 | 6 | 3 | 1 | - | 12 |
| 3,75 | 3 | 2 | - | - | - | 5 |
| nх | 5 | 11 | 13 | 12 | 9 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 10
Дана корреляционная таблица.
| У | Х | |||||
| 45 | 55 | 65 | 75 | 85 | nу | |
| 12,5 | 5 | 10 | - | - | - | 15 |
| 17,5 | 7 | 7 | 27 | - | - | 41 |
| 22,5 | - | 26 | 40 | 24 | - | 90 |
| 27,5 | - | - | 20 | 10 | 4 | 34 |
| 32,5 | - | - | - | 8 | 12 | 20 |
| nх | 12 | 43 | 87 | 42 | 16 | n = 200 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 11
Дана корреляционная таблица.
| У | Х | |||||||
| 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | nу | |
| 2,5 | 7 | 4 | 2 | - | - | - | - | 13 |
| 7,5 | - | 6 | 8 | 6 | 2 | - | - | 22 |
| 12,5 | - | 5 | 8 | 20 | 14 | 10 | 2 | 59 |
| 17,5 | - | - | 2 | 5 | 3 | 4 | 6 | 20 |
| 22,5 | - | - | - | - | - | 2 | 4 | 6 |
| nх | 7 | 15 | 20 | 31 | 19 | 16 | 12 | n = 120 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 12
Дана корреляционная таблица.
| У | Х | |||||||
| 30 | 40 | 50 | 60 | 70 | 80 | 90 | nу | |
| 0 | - | - | - | - | - | 4 | 6 | 10 |
| 6 | - | - | - | 6 | 6 | 8 | - | 20 |
| 12 | - | 1 | 2 | 14 | 3 | - | - | 20 |
| 18 | 1 | 5 | 18 | 2 | - | - | - | 26 |
| 24 | - | 4 | 10 | 2 | - | - | - | 16 |
| 30 | 1 | 5 | 2 | - | - | - | - | 8 |
| nх | 2 | 15 | 32 | 24 | 9 | 12 | 6 | n = 100 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 13
Дана корреляционная таблица.
| У | Х | |||||
| 45 | 55 | 65 | 75 | 85 | nу | |
| 1,125 | - | - | - | 2 | 6 | 8 |
| 1,375 | - | - | 4 | 7 | 4 | 15 |
| 1,625 | 1 | 1 | 7 | 5 | - | 14 |
| 1,875 | 2 | 4 | 1 | - | - | 7 |
| 2,125 | 3 | 3 | - | - | - | 6 |
| nх | 6 | 8 | 12 | 14 | 10 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 14
Дана корреляционная таблица.
| У | Х | |||||
| 32,5 | 37,5 | 42,5 | 47,5 | 52,5 | nу | |
| 5 | 2 | - | - | - | - | 2 |
| 7 | 17 | 10 | 3 | - | - | 30 |
| 9 | 9 | -17 | 24 | 6 | 2 | 58 |
| 11 | 3 | 9 | 16 | 24 | 11 | 63 |
| 13 | - | - | 13 | 12 | 22 | 47 |
| nх | 31 | 36 | 56 | 42 | 35 | n = 200 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 15
Дана корреляционная таблица.
| У | Х | |||||
| 1 | 3 | 5 | 7 | 9 | nу | |
| 0,5 | 3 | 2 | 2 | - | - | 7 |
| 1,5 | 1 | 4 | 3 | - | - | 8 |
| 2,5 | - | 6 | 10 | 4 | - | 20 |
| 3,5 | - | - | 3 | 6 | 1 | 10 |
| 4,5 | - | - | - | 3 | 2 | 5 |
| nх | 4 | 12 | 18 | 13 | 3 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 16
Дана корреляционная таблица.
| У | Х | |||||
| 0 | 8 | 16 | 24 | 32 | nу | |
| 80 | 2 | 2 | 1 | - | - | 5 |
| 90 | 1 | 3 | 6 | - | - | 10 |
| 100 | - | 3 | 5 | 8 | 1 | 17 |
| 110 | - | - | 2 | 7 | 3 | 12 |
| 120 | - | - | - | 2 | 4 | 6 |
| nх | 3 | 8 | 14 | 17 | 8 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 17
Дана корреляционная таблица.
| У | Х | |||||||
| 122,5 | 127,5 | 132,5 | 137,5 | 142,5 | 147,5 | 152,5 | nу | |
| 22,5 | 1 | - | - | - | - | - | - | 1 |
| 25,5 | 3 | 2 | 1 | 1 | - | - | - | 7 |
| 28,5 | - | 6 | 5 | 6 | 1 | - | - | 18 |
| 31,5 | - | 1 | 5 | 7 | 4 | 1 | - | 18 |
| 34,5 | - | - | - | 2 | 2 | 1 | 1 | 6 |
| nх | 4 | 9 | 11 | 16 | 7 | 2 | 1 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 18
Дана корреляционная таблица.
| У | Х | |||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | nу | |
| 130 | 3 | 4 | 3 | - | - | - | - | 10 |
| 150 | 3 | 5 | 6 | 2 | - | - | - | 16 |
| 170 | - | 3 | 8 | 10 | 4 | - | - | 25 |
| 190 | - | - | 2 | 8 | 10 | 6 | - | 26 |
| 210 | - | - | - | 6 | 5 | 2 | 1 | 14 |
| 230 | - | - | - | - | 1 | 2 | 6 | 9 |
| nх | 6 | 12 | 19 | 26 | 20 | 10 | 7 | n = 100 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 19
Дана корреляционная таблица.
| У | Х | ||||||
| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | nу | |
| 10 | 4 | 2 | - | - | - | - | 6 |
| 15 | - | 2 | - | 6 | - | - | 8 |
| 20 | - | - | 2 | - | - | - | 2 |
| 25 | - | - | - | 4 | - | - | 4 |
| 30 | - | - | - | 4 | 6 | - | 10 |
| 35 | - | - | - | - | 6 | 4 | 10 |
| nх | 4 | 4 | 2 | 14 | 12 | 4 | n = 40 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 20
Дана корреляционная таблица.
| У | Х | |||||
| 550 | 650 | 750 | 850 | 950 | nу | |
| 90 | 2 | 1 | - | - | - | 3 |
| 100 | 3 | 4 | 3 | - | - | 10 |
| 110 | - | 3 | 5 | 5 | - | 13 |
| 120 | - | - | 4 | 4 | 4 | 12 |
| 130 | - | - | - | 2 | - | 2 |
| nх | 5 | 8 | 12 | 11 | 4 | n = 40 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 21
Дана корреляционная таблица.
| У | Х | |||||
| 0,1 | 0,25 | 0,40 | 0,55 | 0,70 | nу | |
| 40 | 7 | 5 | 3 | - | - | 15 |
| 50 | 3 | 12 | 4 | 1 | - | 20 |
| 60 | - | 10 | 15 | 3 | - | 28 |
| 70 | - | 1 | 6 | 12 | 5 | 24 |
| 80 | - | - | 2 | 4 | 7 | 13 |
| nх | 10 | 28 | 30 | 20 | 12 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 22
Дана корреляционная таблица.
| У | Х | ||||
| 5 | 10 | 15 | 20 | nу | |
| 10 | 2 | - | - | - | 2 |
| 20 | 5 | 4 | 1 | - | 10 |
| 30 | 3 | 8 | 6 | 3 | 20 |
| 40 | - | 3 | 6 | 6 | 15 |
| 50 | - | - | 2 | 1 | 3 |
| nх | 10 | 15 | 15 | 10 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 23
Дана корреляционная таблица.
| У | Х | |||||
| 65 | 95 | 125 | 155 | 185 | nу | |
| 30 | 5 | - | - | - | - | 5 |
| 40 | 4 | 12 | - | - | - | 16 |
| 50 | - | 8 | 5 | 4 | - | 17 |
| 60 | - | 1 | 5 | 7 | 2 | 15 |
| 70 | - | - | - | - | 2 | 2 |
| nх | 9 | 21 | 10 | 11 | 4 | n = 55 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 24
Дана корреляционная таблица.
| У | Х | ||||||
| 4 | 9 | 14 | 19 | 24 | 29 | nу | |
| 15 | 2 | 3 | - | - | - | - | 5 |
| 25 | - | 7 | 3 | - | - | - | 10 |
| 35 | - | - | 2 | 50 | 2 | - | 54 |
| 45 | - | - | 1 | 10 | 6 | - | 17 |
| 55 | - | - | - | 4 | 7 | 3 | 14 |
| nх | 2 | 10 | 6 | 64 | 15 | 3 | n = 100 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Вариант № 25
Дана корреляционная таблица.
| У | Х | |||||||
| 120,5 | 127,5 | 134,5 | 141,5 | 148,5 | 155,5 | 162,5 | nу | |
| 12,8 | 1 | - | - | - | - | - | - | 1 |
| 15,8 | 2 | 3 | 1 | 2 | - | - | - | 8 |
| 18,8 | - | 5 | 5 | 6 | 1 | - | - | 17 |
| 21,8 | - | 1 | 5 | 7 | 4 | 1 | - | 18 |
| 24,8 | - | - | - | 2 | 2 | 1 | 1 | 6 |
| nх | 3 | 9 | 11 | 17 | 7 | 2 | 1 | n = 50 |
Найти: а) выборочный коэффициент корреляции; б) выборочные уравнения прямых регрессии.
Контрольные вопросы
1. Какую зависимость называют статистической?
2. Какую зависимость называют корреляционной?
3. Что называют условным средним?
4. В качестве каких оценок принимают условные средние?
5. Какое уравнение называют выборочным уравнением регрессии?
6. Какую функцию называют выборочной регрессией?
7. Что называют выборочной линией регрессии?
8. Что называют выборочным коэффициентом регрессии?
9. Как находятся параметры выборочного уравнения прямой линии регрессии по сгруппированным данным?
Приложения
Приложение 1

Приложение 2
Таблица значений функции 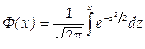
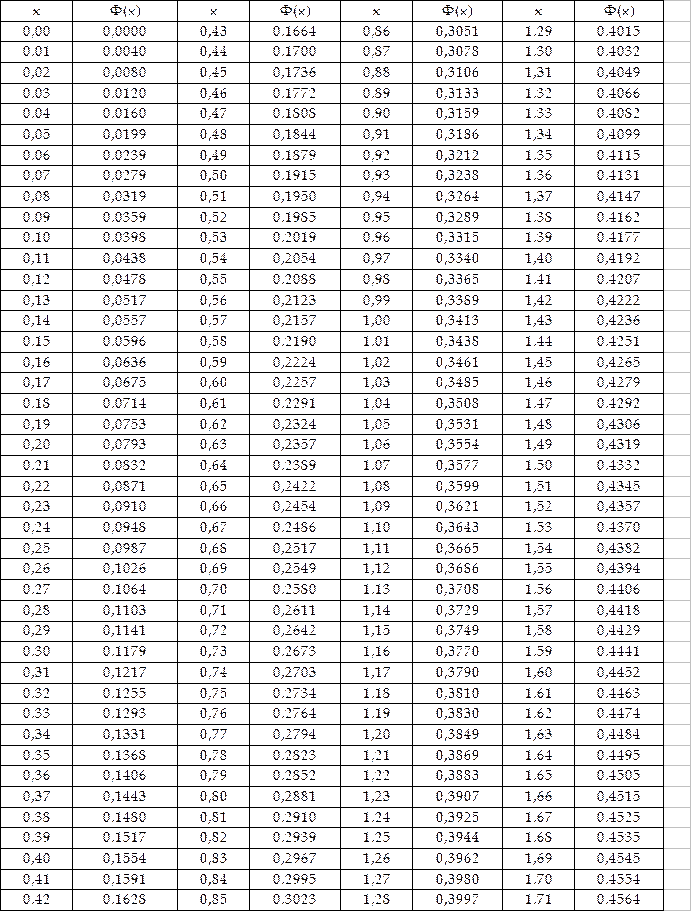
Продолжение приложения 2
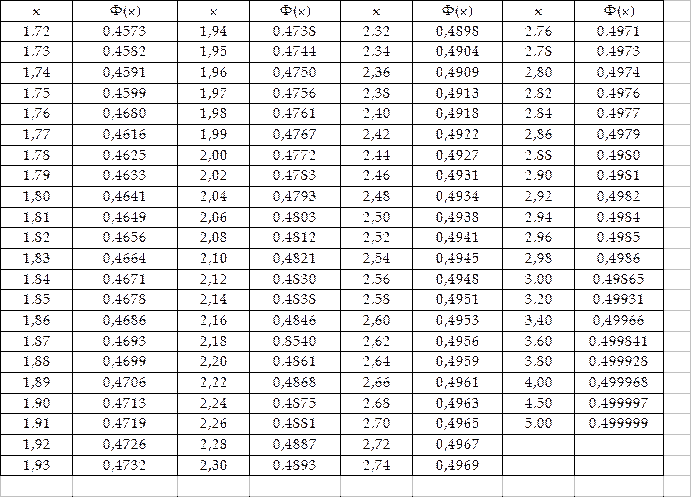
Приложение 3
Таблица значений 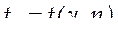
| n |
| n |
| ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 5 | 2,78 | 4,60 | 8,61 | 20 | 2,093 | 2,861 | 3,883 |
| 6 | 2,57 | 4,03 | 6,86 | 25 | 2,064 | 2,797 | 3,745 |
| 7 | 2,45 | 3,71 | 5,96 | 30 | 2,045 | 2,765 | 3,659 |
| 8 | 2,37 | 3,50 | 5,41 | 35 | 2,032 | 2,720 | 3,600 |
| 9 | 2,31 | 3,36 | 5,04 | 40 | 2,023 | 2,708 | 3,558 |
| 10 | 2,26 | 3,25 | 4,78 | 45 | 2,016 | 2,692 | 3,527 |
| 11 | 2,23 | 3,17 | 4,59 | 50 | 2,009 | 2,679 | 3,502 |
| 12 | 2,20 | 3,11 | 4,44 | 60 | 2,001 | 2,662 | 3,464 |
| 13 | 2,18 | 3,06 | 4,32 | 70 | 1,996 | 2,649 | 3,439 |
| 14 | 2,16 | 3,01 | 4,22 | 80 | 1,001 | 2,640 | 3,418 |
| 15 | 2,15 | 2,98 | 4,14 | 90 | 1,987 | 2,633 | 3,403 |
| 16 | 2,13 | 2,95 | 4,07 | 100 | 1,984 | 2,627 | 3,392 |
| 17 | 2,13 | 2,92 | 4,02 | 120 | 1,980 | 2,617 | 3,374 |
| 18 | 2,11 | 2,90 | 3,97 | 
| 1,960 | 2,576 | 3,291 |
| 19 | 2,10 | 2,88 | 9,92 | ||||
Приложение 4
Таблица значений 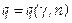
| n |
| n |
| ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 5 | 1,37 | 2,67 | 5,64 | 20 | 0,37 | 0,58 | 0,88 |
| 6 | 1,09 | 2,01 | 3,88 | 25 | 0,32 | 0,49 | 0,73 |
| 7 | 0,92 | 1,62 | 2,98 | 30 | 0,28 | 0,43 | 0,63 |
| 8 | 0,80 | 1,38 | 2,42 | 35 | 0,26 | 0,38 | 0,56 |
| 9 | 0,71 | 1,20 | 2,06 | 40 | 0,24 | 0,35 | 0,50 |
| 10 | 0,65 | 1,08 | 1,80 | 45 | 0,22 | 0,32 | 0,46 |
| 11 | 0,59 | 0,98 | 1,60 | 50 | 0,21 | 0,30 | 0,43 |
| 12 | 0,55 | 0,90 | 1,45 | 60 | 0,188 | 0,269 | 0,38 |
| 13 | 0,52 | 0,83 | 1,33 | 70 | 0,174 | 0,245 | 0,34 |
| 14 | 0,48 | 0,78 | 1,23 | 80 | 0,161 | 0,226 | 0,31 |
| 15 | 0,46 | 0,73 | 1,15 | 90 | 0,151 | 0,211 | 0,29 |
| 16 | 0,44 | 0,70 | 1,07 | 100 | 0,143 | 0,198 | 0,27 |
| 17 | 0,42 | 0,66 | 1,01 | 150 | 0,115 | 0,160 | 0,211 |
| 18 | 0,40 | 0,63 | 0,96 | 200 | 0,099 | 0,139 | 0,185 |
| 19 | 0,39 | 0,60 | 0,92 | 250 | 0,089 | 0,120 | 0,162 |
Литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебн. пособие для вузов. - М: Высш.шк. , 2003. – 479 с.:ил.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособие для вузов. М: Высш.шк., 2003. – 405 с.:ил.
3. Вентцель Е.С. Теория вероятностей. Учебн. пособие для вузов. – М: Высш.шк. , 2002. – 575 с.:ил.
4. Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. Учебн. пособие для втузов. - М: Высш.шк. , 2000. – 480 с.:ил.
5. Кромер Н.Ш. Теория вероятностей. Учебн. пособие для вузов. – М: ЮНИТИ-ДАНА , 2001. – 543 с.
Дата добавления: 2019-09-13; просмотров: 502; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!