Уравнения прямой в пространстве
1. Уравнения прямой, проходящей через точку 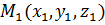 и параллельной вектору
и параллельной вектору 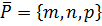 .
.
Пусть 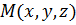 произвольная точка прямой, тогда
произвольная точка прямой, тогда 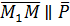 ,
,
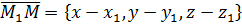 и по условию коллинеарности векторов (см.2.1.2)
и по условию коллинеарности векторов (см.2.1.2)

Уравнения (5) называются каноническими уравнениями прямой.
Вектор 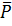 называется направляющим вектором прямой.
называется направляющим вектором прямой.
2. Параметрические уравнения прямой получим, приняв каждое из отношений (5) параметру t:
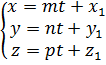 (6)
(6)
3. Уравнения прямой, проходящей через две точки 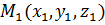 и
и 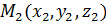 :
:

4. Общие уравнения прямой:

Угол между прямой 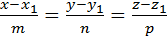 и плоскостью Ax+By+Cz+D=0
и плоскостью Ax+By+Cz+D=0
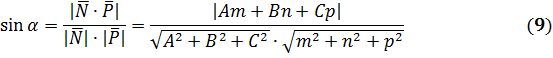
Уравнения прямой на плоскости.
Уравнения прямой с угловым коэффициентом.

Угловой коэффициент 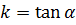 , где -
, где - 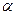 угол наклона прямой к оси ОХ.
угол наклона прямой к оси ОХ.
Общее уравнение прямой
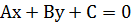
Уравнение прямой в отрезках на осях Х
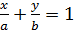 , где a и b – величины отрезков, отсекаемых прямой на осях координат.
, где a и b – величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две заданные точки 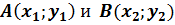

Уравнения пучка прямых, проходящих через заданную точку 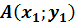 :
:

Угол 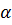 , отсчитанный против часовой стрелки от прямой
, отсчитанный против часовой стрелки от прямой 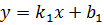 до прямой
до прямой 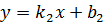 определяется формулой
определяется формулой

Условие перпендикулярности 
Условие параллельности 
Решение типового варианта.
Задача№3.
Даны координаты точек A,B,C,D.
Найти: а) угол между векторами 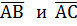 ;
;
б) площадь треугольника АВС;
в) высоту треугольника АВС, опущенную из вершины С;
|
|
|
г) объем пирамиды ABCD;
д) высоту пирамиды ABCD, опущенную из вершины D на основание АВС.
А(-1,2,3), В(4,-1,3), С(2,0,5), D(7,8,-1)
Решение:
а) 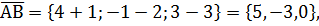
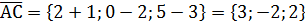
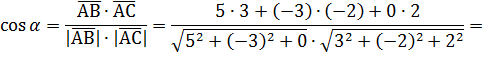
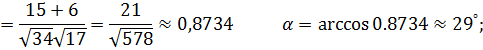
б) Площадь треугольника АВС, построенного на векторах 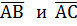
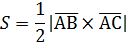
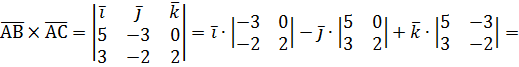
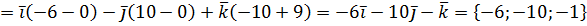
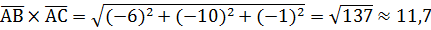
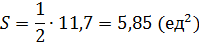
в) Известно, что 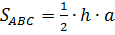 , значит
, значит 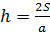 ,
, 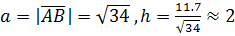
г) 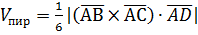
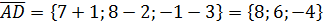
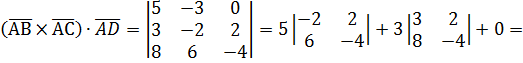
=5(8-12)+3(-12-16)=-20-84= - 104
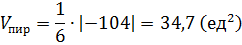
д) 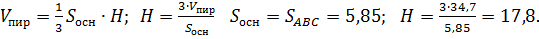
Задача №4.
Составить уравнение плоскости проходящей через точку А и перпендикулярно вектору 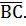 А(1;4;-2), B(6;7;0), C(8;6;3).
А(1;4;-2), B(6;7;0), C(8;6;3).
Решение.
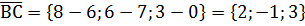 –нормальный вектор к искомой плоскости (см. 2.2.1.)
–нормальный вектор к искомой плоскости (см. 2.2.1.)
Пусть точка M(x,y,z) – произвольная точка искомой плоскости, 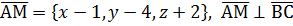 и по условию перпендикулярности векторов 2(х-1)+(-1)(y-4)+3(z+2)=0, 2x-2-y+4+3z+6=0,
и по условию перпендикулярности векторов 2(х-1)+(-1)(y-4)+3(z+2)=0, 2x-2-y+4+3z+6=0,
2x-y+3z+8=0 - уравнение искомой плоскости.
Задача №5.
Даны координаты точек A,B,C,D.
Найти: а) уравнение плоскости, проходящей через точки А,В,С;
б) расстояние точки D до плоскости АВС;
в) угол между плоскостью АВС и плоскостью 5x-3y+7z-3=0
А(1;1;3), В(-2;1;4), С(-1;2;3), D(-1;1;5).
Решение:
а) В искомой плоскости возьмём некоторую точку M(x,y,z), тогда вектора
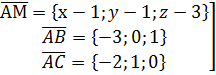 лежат в искомой плоскости, значит компланарны.
лежат в искомой плоскости, значит компланарны.
Запишем условие компланарности трёх векторов (см. 2.1.4.):
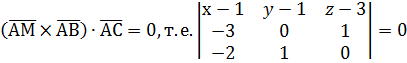
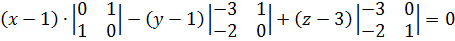
(x-1)(0-1)-(y-1)(0+2)+(z-3)(-3+0)=0
-x+1-2y+2-3z+9=0
X+2y+3z-12=0 – уравнение плоскости АВС, её нормальный
|
|
|
вектор 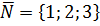 .
.
б) Найдем расстояние точки D до плоскости АВС. (см. 2.2.1. формула (4))
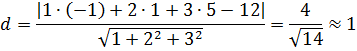
в) угол между плоскостями равен углу между их нормальными векторами
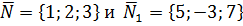
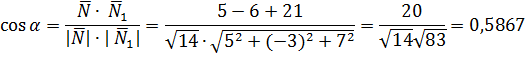
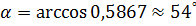
Задача №6.
Прямая 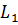 задана общими уравнения.
задана общими уравнения.
Найти: а) канонические и параметрические уравнения прямой 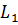 ;
;
б) найти угол между прямой 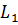 и прямой
и прямой 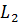 :
: 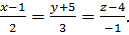
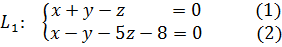
Решение:
а) Прямая 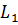 задана как пересечение плоскостей (1) и (2) с нормальными векторами соответственно.
задана как пересечение плоскостей (1) и (2) с нормальными векторами соответственно. 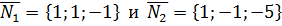 .
.
Направляющий вектор прямой 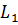
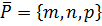 ортогонален
ортогонален 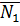 и
и 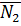 , найдем его как векторное произведение (см. 2.1.3).
, найдем его как векторное произведение (см. 2.1.3).
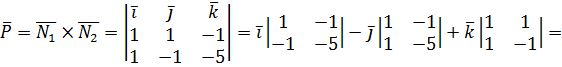
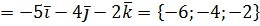
Для простоты возьмём направляющим вектором противоположный
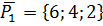 Найдем какую-нибудь точку, лежащую на
Найдем какую-нибудь точку, лежащую на 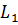 , т.е. удовлетворяющую условиям (1) и (2).
, т.е. удовлетворяющую условиям (1) и (2).
Пусть z=0, тогда 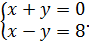 Сложим уравнение, получим 2х=8, х=4, значит y=-4. Точка
Сложим уравнение, получим 2х=8, х=4, значит y=-4. Точка 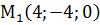 принадлежит искомой прямой, параллельной вектору
принадлежит искомой прямой, параллельной вектору 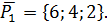 Пусть точка M(x,y,z) некоторая точка искомой, тогда вектор
Пусть точка M(x,y,z) некоторая точка искомой, тогда вектор 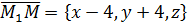 коллинеарен вектору
коллинеарен вектору 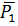 . Запишем условие коллинеарности двух векторов (см.2.2.2)
. Запишем условие коллинеарности двух векторов (см.2.2.2)
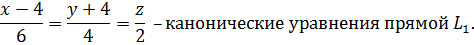
Тогда параметрические уравнения прямой 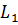 имеют вид (см. 2.2.2):
имеют вид (см. 2.2.2):
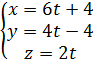
б) Угол между прямыми 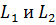 равен углу между их направляющими векторами
равен углу между их направляющими векторами 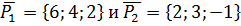
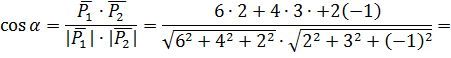
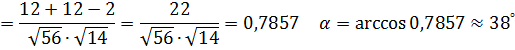
Задача №7.
Найти точку пересечения прямой и плоскости. Найти угол между прямой и плоскостью. 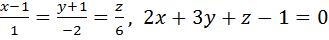
|
|
|
Решение:
Уравнения прямой запишем в параметрическом виде (см. 2.2.2):
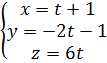 Выражения подставим в уравнения плоскости, решим его относительно t:
Выражения подставим в уравнения плоскости, решим его относительно t:
2(t+1)+3(-2t-1)+6t-1=0, 2t+2-6t-3+6t-1=0, 2t=2, t=1.
Чтобы найти точку пересечения прямой и плоскости 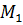 , подставим найденное значение t в параметрические уравнения, получим x=2, y=-3, z=6, т.е.
, подставим найденное значение t в параметрические уравнения, получим x=2, y=-3, z=6, т.е. 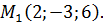 Угол
Угол 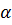 между прямой и плоскостью находим по формуле (9) пункта 2.2.2. Направляющий вектор прямой
между прямой и плоскостью находим по формуле (9) пункта 2.2.2. Направляющий вектор прямой 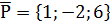 , нормальный вектор плоскости
, нормальный вектор плоскости 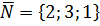 .
.
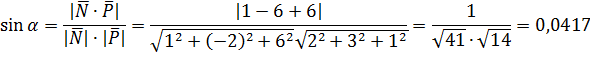
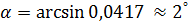
Задача №8.
Даны координаты точек А,В,С.
Найти: а) уравнение медианы AD;
б) уравнение высоты АЕ;
в) угол между AD и АЕ;
г) уравнение прямой, проходящей через точку С параллельно АВ.
А (-4;2), В (6;-4), С (4;10).
Решение: 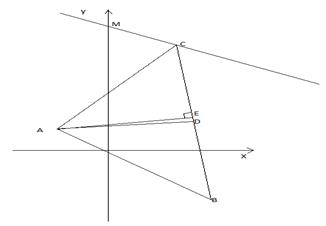
а) Точка D – середина отрезка ВС, её координаты (см. 2.1.1.):
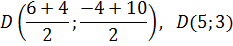
Уравнение медианы AD находим как уравнение прямой, проходящей через две точки (см. (11) в пункте 2.2.3.).
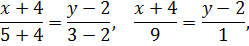
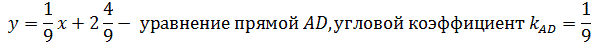
б) Чтобы найти уравнение высоты АЕ, составим уравнение перпендикулярной ей СВ (см. (11)).
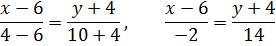
-7(x-6)=y+4, y=-7x+38 - уравнение СВ, 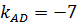
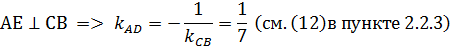
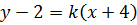 и поставим вместо k значение
и поставим вместо k значение 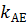
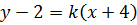
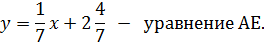
в) По формуле (13) пункта 2.2.3 найдем угол между АЕ и AD, в нашем случае
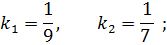
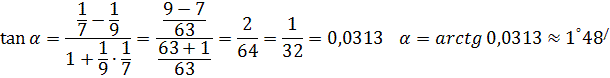
г) Найдем уравнение прямой АВ (см. (11)
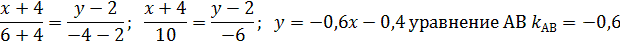
Искомая прямая 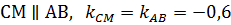 (см. (15) пункт 2.2.3)
(см. (15) пункт 2.2.3)
|
|
|
Запишем уравнение пучка прямых, проходящих через точку С:
y-10=k(x-4) и подставим вместо k значение 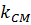 .
.
y-10=-0,6(x-4)
y=-0,6x+12,4 уравнение прямой СМ.
Дата добавления: 2019-09-13; просмотров: 148; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
