Векторная алгебра. Аналитическая геометрия.
Векторная алгебра.
Сложение векторов. Умножение вектора на скаляр.
Вектором называется направленный отрезок 
, в котором точка А рассматривается как начало, а точка В - как конец вектора.
Модуль (длина) вектора обозначается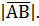 
В параллелограмме, построенном на данных и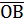 
, одна вектор – диагональ есть сумма векторов 
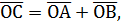а другая вектор-диагональ есть разность векторов 
.
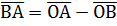Произведением вектора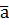 
на число (скаляр) m называется вектор, имеющий длину 
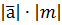и направленный одинаково 
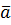с (при m > 0) или противоположно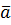
(при m<0).
Если известны координаты начала А 
и конца вектора В 
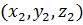, то координаты вектора можно найти по правилу
, 
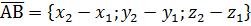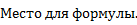
координаты середины отрезка АВ:
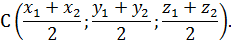
Если векторы заданы в координатной форме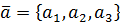 
, 
, 
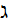- константа, то
1) 
- координаты суммы (разности) векторов;
2) 
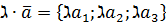- координаты произведения вектора на число;
3) 
- длина вектора .
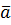Скалярное произведение двух векторов.
Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Свойства скалярного произведения:
1. 
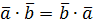- переместительный закон.
2. 
– распределительный закон.
3. 
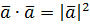, поэтому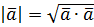 
4. Если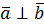 
, то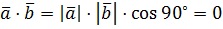 
5. Если векторы заданы координатами 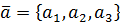и , то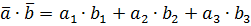 
Угол между векторами:
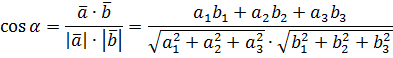
Условие коллинеарности векторов 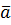и 
:
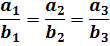
Условие ортогональности векторов 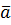и :
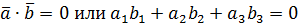
Векторное произведение двух векторов.
Определение: Векторным произведением вектора 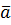на вектор , называется вектор, обозначаемый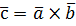 
и определяемы следующими тремя условиями:
|
|
|
1) 
;
2) , , 
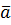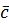образуют правую тройку, т.е. из конца третьего вектора движение первого ко второму по кратчайшему пути наблюдается против часовой стрелки;
3) 
, где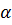 
- угол между векторам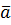и и .
Свойства векторного произведения:
1. 
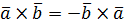
2. 
3. Если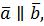 
то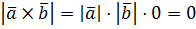 
Векторные произведение векторов:
Если векторы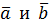 
заданы в координатной форме 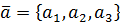и , то 
Площадь параллелограмма, построенного на векторах 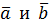, численно равна модулю их численного произведения:
.
Площадь треугольника, построенного на векторах :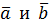
.
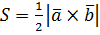Смешанное произведение трёх векторов
Определение: Смешенным произведением векторов 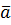, и 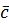называется выражение вида 
.
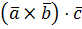Если векторы 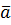, и 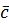заданы своими координатами, то
.
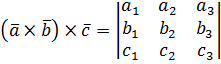Свойства смешенного произведения:
1. От перестановки двух соседних сомножителей смешенное произведение меняет знак:
.
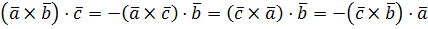2. Если два из трех данных векторов равны или коллинеарные, то их смешенное произведение равно нулю.
3. Имеет место тождество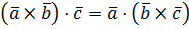 
, поэтому смешенное произведение можно записать в виде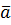 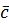, т.е. без знаков действий и без скобок.
Объем параллелепипеда, построенного на векторах 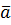, и :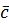
|
|
|
.
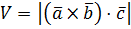Объем пирамиды, построенной на векторах 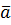, и :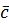
.
Условия компланарности трёх векторов:
Есл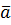и , и 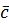компланарны, то 
и наоборот.
Аналитическая геометрия.
Уравнения плоскости.
1.Уравнение плоскости, проходящей через точку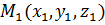 
и перпендикулярной к вектору 
.
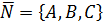Пусть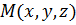 
произвольная точка плоскости,
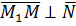и по условию ортогональности векторов (см. 2.1.2.)
(1)
2.Общее уравнение плоскости:
(2)
Вектор 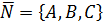называется нормальным вектором к плоскости (1) и (2).
3.Уравнение плоскости в отрезках на осях:
(3)
Пусть заданы две плоскости Ax+By+Cz+D=0 и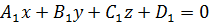 
1.Угол, образованный двумя плоскостями равен углу между их нормальными векторами:
2.Условие параллельности плоскостей
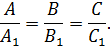
3.Условие перпендикулярности плоскостей:
Расстояние точки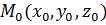 
от плоскости Ax+By+Cz+D=0:
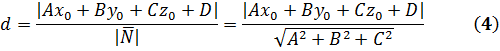
Дата добавления: 2019-09-13; просмотров: 307; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!