Формирование целых чисел в позиционных системах счисления
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением цифры называют замену её следующей по величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры - 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 - замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета [4]:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Применяя это правило, запишем первые десять целых чисел
- в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
- в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
- в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
- восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Принципы кодирования чисел в позиционных системах счисления
Чтобы перевести число, скажем, 12345N, из системы счисления с основанием 
в десятичную систему, нужно умножить значение каждой цифры на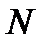 
в степени, равной ее разряду:
P XuvvP4PLvwAAAP//AwBQSwMEFAAGAAgAAAAhAMI51JzdAAAACgEAAA8AAABkcnMvZG93bnJldi54 bWxMj8FOwzAQRO9I/IO1SNxaJ0YOJcSpKiSOIJGCxNGNTRyw11HstuHvWU5wXM3TzNtmuwTPTnZO Y0QF5boAZrGPZsRBwev+cbUBlrJGo31Eq+DbJti2lxeNrk0844s9dXlgVIKp1gpczlPNeeqdDTqt 42SRso84B53pnAduZn2m8uC5KIqKBz0iLTg92Qdn+6/uGBR0ftc/if2zu33/LFF0b8lhmZS6vlp2 98CyXfIfDL/6pA4tOR3iEU1iXoGU5Q2hClZCSGBEVJW8A3YgVG6Atw3//0L7AwAA//8DAFBLAQIt ABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10u eG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5y ZWxzUEsBAi0AFAAGAAgAAAAhANdfySJFAwAAVAYAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9E b2MueG1sUEsBAi0AFAAGAAgAAAAhAMI51JzdAAAACgEAAA8AAAAAAAAAAAAAAAAAnwUAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAACpBgAAAAA= " adj="-1941,27076" fillcolor="#ff9" stroked="f">
| N0 = 1 |
|
|
|
1 2 3 4 5N = 1·N4 + 2·N3 + 3·N2 + 4·N1 + 5·N0
· последняя цифра записи числа в системе счисления с основанием – это остаток от деления этого числа на ;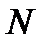
· две последние цифры – это остаток от деления на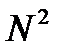 
, и т.д.
Пример. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход: вспомним алгоритм перевода числа из десятичной системы в систему с основанием N, из него следует, что младшая цифра результата – это остаток от деления исходного числа на N, а две младших цифры – это остаток от деления на N 2 и т.д. В данном случае N =4, остаток от деления числа на N 2=16 должен быть равен 114 = 5. Потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16.
Решение (через десятичную систему): Общий вид чисел, которые дают остаток 5 при делении на 16 k·16+5, где k – целое неотрицательное число (0, 1, 2, …). Среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при k=0) и 21 (при k=1). Таким образом, верный ответ – 5, 21.
|
|
|
Пример.Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Общий подход: Здесь обратная задача – неизвестно основание системы счисления, мы обозначим его через N. Поскольку последняя цифра числа – 2, основание должно быть больше 2, то есть N >2. Вспомним алгоритм перевода числа из десятичной системы в систему с основанием N, из него следует, что младшая цифра результата – это остаток от деления исходного числа на N.
Решение: Итак, нужно найти все целые числа N ≥3, такие что остаток от деления 23 на N равен 2, или (что-то же самое), 23=k · N+2 (*), где k – целое неотрицательное число (0, 1, 2, …); сложность в том, что и k, и N неизвестны, однако здесь нужно «играть» на том, что это натуральные числа;из формулы (*) получаем k · N =21, так что задача сводится к тому, чтобы найти все делители числа 21, которые больше 2; в этой задаче есть только три таких делителя: N=3,7 и 21; таким образом, верный ответ – 3, 7, 21.
Пример. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31оканчивается на 11.
|
|
|
Общий подход: Неизвестно основание системы счисления, мы обозначим его через N . Пока будем считать, что запись числа 31 в системе с основанием N состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через k) нужно найти:
2 1 0 ← разряды
31 k 1 1N = k·N2 + N1 + N0 = k·N2 + N + 1
Можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить, как 31=k·N2+N+1 при некотором целом k; например, для числа с пятью разрядами получаем:
4 3 2 1 0 ← разряды
31 = k4 k3 k2 1 1N = k4·N4 + k3·N3 + k2·N2 + N1 + N0= k·N2 + N + 1
Для k=k4N2+k3N+k2 (из первых трех слагаемых вынесли общий множитель N2).
Решение: Итак, нужно найти все целые числа N≥2, такие что 31=k · N 2+N+1 (**), где k – целое неотрицательное число (0, 1, 2, …); сложность в том, что и k, и N неизвестны, однако здесь нужно «играть» на том, что это натуральные числа. Из формулы (**) получаем (k · N+1)N =30, так что задача сводится к тому, чтобы найти все делители N числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом k, то есть,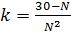 
– целое число выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30, из всех этих делителей только для 2, 3, 5 и 30 значение 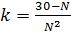– целое число (оно равно соответственно 7, 3, 1 и 0). Таким образом, верный ответ – 2, 3, 5, 30.
|
|
|
Дата добавления: 2019-09-08; просмотров: 236; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!