Интегрирование рациональных дробей.
Дробно-рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочленов, т. е.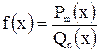 
, где 
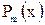- многочлен степени 
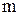, a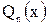 
- многочлен степени 
.
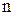Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т.е.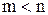 
; в противном случае (если 
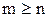) рациональная дробь называется неправильной.
Всякую неправильную рациональную дробь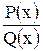 
можно, путем деления числителя на знаменатель, представить в виде суммы многочлена 
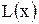и правильной рациональной дроби 
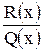, то есть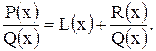 
Например,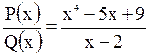 
- неправильная рациональная дробь. Разделим числитель на знаменатель. Получим частное 
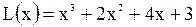и остаток 
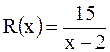. Следовательно, 
.
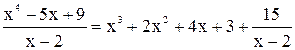Теорема 3. Пусть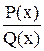 
- правильная рациональная дробь с вещественными коэффициентами, знаменатель которой имеет вид
.
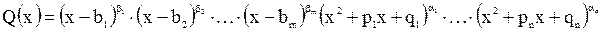Тогда для этой дроби справедливо следующее разложение на сумму простейших дробей:
В этом разложении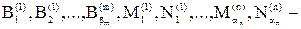 
некоторые вещественные постоянные, часть из которых может быть равна нулю.
Поясним формулировку теоремы на следующих примерах:
1. 
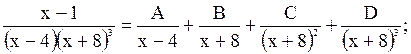
2. 
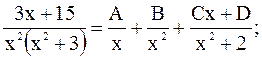
3. 
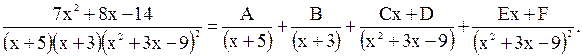
Для нахождения неопределенных коэффициентов в равенстве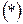 
можно применить метод сравнивания коэффициентов. Суть метода такова:
1. В правой части равенства приведем к общему знаменателю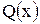 
; в результате получим тождество 
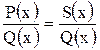, где 
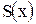- многочлен с неопределенными коэффициентами.
|
|
|
2. Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т. е.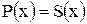 
.
3. Приравнивая коэффициенты при одинаковых степенях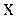 
в обеих частях тождества, получим систему линейных уравнений, из которой и определим искомые коэффициенты.
Пример 4.
Представить дробь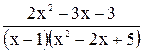 
в виде суммы простейших дробей.
В силу рассмотренной теоремы имеем:
.
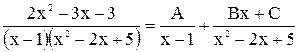Приведём правую часть к общему знаменателю:
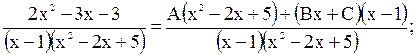
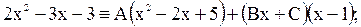
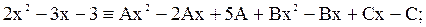
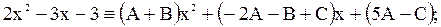
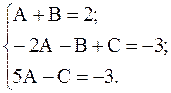
Находим, что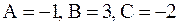 
. Следовательно,
.
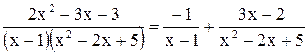Теперь мы подготовлены к тому, чтобы в общем виде решить проблему об интегрировании рациональной дроби с вещественными коэффициентами.
Прежде всего, отметим, что эта проблема сводится к проблеме интегрирования только правильной рациональной дроби, ибо всякую неправильную рациональную дробь можно (посредством деления числителя на знаменатель «столбиком») представить в виде суммы алгебраического многочлена и правильной рациональной дроби.
Интегрировать многочлен мы умеем (напомним, что неопределенный интеграл от многочлена представляет собой некоторый многочлен степени, на единицу более высокой). Остается научиться интегрировать правильную рациональную дробь. Таким образом, проблема интегрирования правильной рациональной дроби сводится к интегрированию простейших дробей следующих четырех типов:
|
|
|
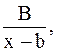I 
II 
III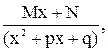 
IV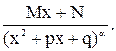 
Здесь a = 2,3, ...; b = 2,3, ...; В, М, N , b, р и q - некоторые вещественные числа, причем трехчлен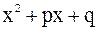 
не имеет вещественных корней, т. е. 
.
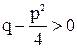Докажем, что каждая из четырех указанных дробей интегрируема в элементарных функциях.
Дроби вида I и II элементарно интегрируются при помощи подстановки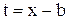 
. Мы получим
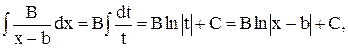
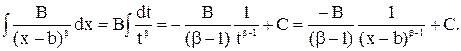
Для вычисления интеграла от дроби вида III представим квадратный трехчлен в виде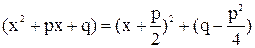 
учитывая, что 
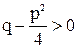, введем в рассмотрение вещественную постоянную 
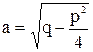. Сделав подстановку 
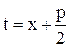, будем иметь
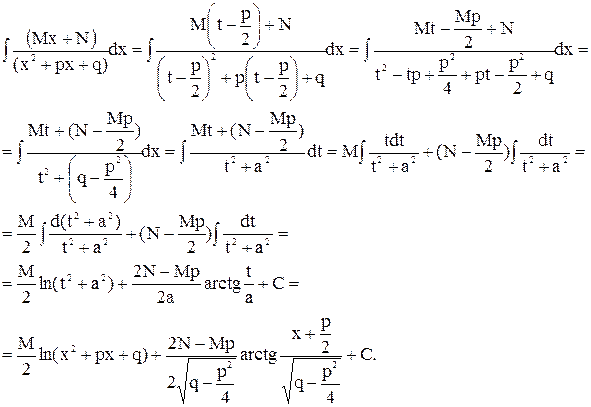
Остается вычислить интеграл от дроби вида IV. Используя введенные выше обозначения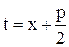 
, будем иметь
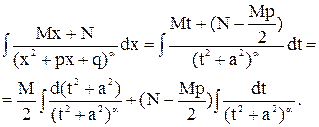
Введем обозначения
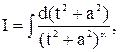
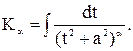
Интересующий нас интеграл будет вычислен, если будут вычислены интегралы I и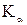 
. Интеграл I берется элементарно:
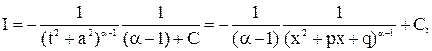
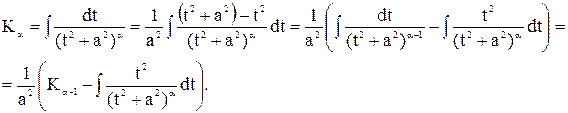
К последнему интегралу применим интегрирование по частям:
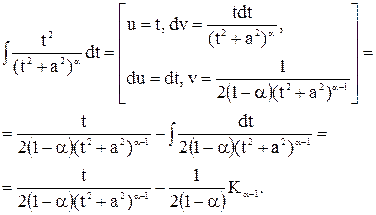
В результате получаем
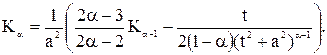
Итак, нами вычислены интегралы от всех четырех простейших дробей и доказано, что каждый из этих интегралов представляет собой элементарную функцию. Тем самым мы приходим к следующей теореме, исчерпывающей проблему интегрирования рациональной дроби.
|
|
|
Теорема 4. Всякая рациональная дробь интегрируема в элементарных функциях.
Сформулируем общее правило интегрирования рациональных дробей:
1. Если дробь неправильная, то представить её в виде суммы многочлена и правильной дроби;
2. Разложив знаменатель правильной рациональной дроби на множители, представить её в виде суммы простейших рациональных дробей;
3. Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример 5. Найти интегралы:
1) 
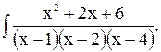
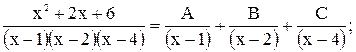
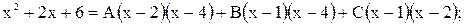
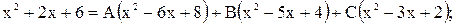
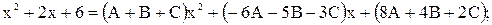
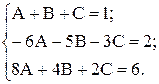
Из системы находим,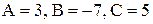 
тогда
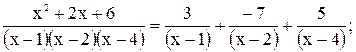
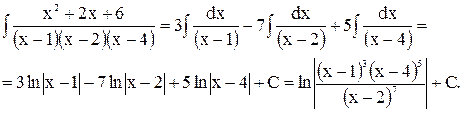
2) 
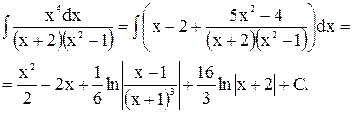
Дата добавления: 2019-09-02; просмотров: 289; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!