Метод непосредственного интегрирования.
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»):
, а- число;
- число;
;
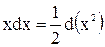и т.д.
Формула 
часто используется при вычислении интегралов.
Пример 1.
Вычислить интеграл и проверит результат:
1. 
2. 
3. 
Метод подстановки или замена переменной.
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.
Теорема 1. Пусть функция 
определена и дифференцируема на некотором множестве X, а T - множество значений этой функции. Пусть далее для функции 
существует на множестве Т первообразная функция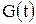 
, то есть
Тогда всюду на множестве Х для функции 
существует первообразная функция, равная 
, то есть
Доказательство.
Для доказательства этого утверждения достаточно воспользоваться правилом дифференцирования сложной функции:
и учесть, что, по определению первообразной, 
Предположим теперь, что нам требуется вычислить интеграл
|
|
|
В ряде случаев удаётся выбрать в качестве новой переменной такую дифференцируемую функцию 
, что имеет место равенство
причём функция легко интегрируется, то есть интеграл
просто вычисляется. Доказанное выше утверждение позволяет нам написать следующую формулу для интеграла 
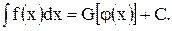
На основании выше изложенного получаем формулу интегрирования подстановкой
.
Данная формула также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования 
назад к переменной 
.
Пример 2.
1) 
2) 
3) 
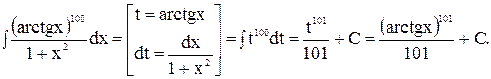
4) 
5) 
Интегрирование по частям.
К числу весьма эффективных методов интегрирования относится метод интегрирования по частям. Этот метод основывается на следующем утверждении.
Теорема 2. Пусть каждая из функций 
и 
дифференцируема на множестве Х, и, кроме того, на этом множестве существует первообразная для функции 
. Тогда на множестве Х существует первообразная и для функции 
, причём справедлива формула
.
Замечание. Определение дифференциала позволяет записать предыдущую формулу в виде:
. (1)
|
|
|
Доказательство. Для доказательства запишем формулу для производной произведения двух функций:
.
Умножим это равенство на 
и возьмём интеграл от обеих частей полученного таким путём равенства. Так как по условию для всех х из множества Х существует 
и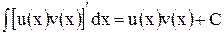 
, то для всех 
из множества Х существует и интеграл 
.
Формула (1) сводит вопрос о вычислении интеграла 
к вычислению интеграла 
. В ряде конкретных случаев этот последний интеграл без труда вычисляется.
Вычисление интеграла 
посредством применения формулы (1) и называется интегрированием по частям.
Пример 3.
1) 
2) 
Практика показывает, что большая часть интегралов, берущихся посредством интегрирования по частям, может быть разбита на следующие три группы:
1) К первой группе относятся интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций: 
, 
, 
, 
, 
, 
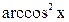, . . . Для вычисления интегралов первой группы следует применить формулу (1), полагая в ней 
равной одной из указанных выше функций.
2) Ко второй группе относятся интегралы вида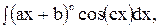 
, где a, b, c – некоторые постоянные, n – любое целое положительное число. Интегралы второй группы берутся путём n – кратного применения формулы интегрирования по частям (1), причём в качестве 
всякий раз требуется брать 
в соответствующей степени. После каждого интегрирования по частям эта степень будет понижаться на единицу.
|
|
|
3) К третьей группе относятся интегралы вида 
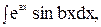
. . . Обозначая любой из интегралов этой группы через I и производя двукратное интегрирование по частям, мы составим для I уравнение первого порядка.
Конечно, указанные три группы не исчерпывают всех без исключения интегралов, берущихся по средствам интегрирования по частям. Приведём примеры интеграла, не входящего ни в одну из перечисленных трёх групп, но вычисляемого по формуле (1).
Дата добавления: 2019-09-02; просмотров: 298; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!