Помехоустойчивость фазовой манипуляции при флуктуационных помехах и отсутствии замираний

Как и ранее,  будем считать, что флуктуационная помеха имеет нормальный закон распределения. Такая по­меха, пройдя через избирательный тракт приемника с резонанс­ной частотой ω₁, будет представлять собой узкополосный случай­ный процесс вида

 

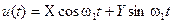                                      .                        (10.24)

Величины X и Y есть медленно меняющиеся функции времени, описываемые нормальным законом распределения

;                                                                                                        

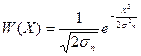                                                                         (10.25)                                                                                                      

,         

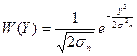где 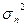  — дисперсия величин X и Y , совпадающая с диспер­сией помехи на входе фазового детектора.

Сумму сигнала (10.23) н помехи (10.24) можно представить в следующем виде:

 

;

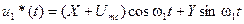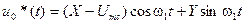.                                     (10.26)

Из (10.26) видно, что помеха имеет синфазную с сигналом сос­тавляющую, амплитуда которой равна X , атакже ортогональную с сигналом составляющую, амплитуда которой равна Y . При этом колебание u ₁ *( t ) соответствует посылке u ₁ ( t ), а колебание u_о*(t) — активной паузе u_o ( t ).

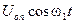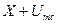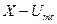На фазовый детектор приемника кроме колебаний вида (10.26) поступает колебание опорной частоты  синхронное и синфазное с принимаемым сигналом ФТ. Это позволяет пол­ностью исключить действие ортогональной к сигналу соответству­ющей помехи. Фазовый детектор реагирует лишь на амплитуду сигнала U_mc и амплитуду синфазной составляющей помехи X . Совершенно ясно, что амплитуды и также будут описываться нормальным законом распределения

;

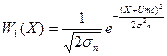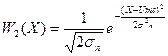.                              (10.27)

 

На рис. 10.7 приведены кривые плотности вероятности, пост­роенные по формулам (10.27), из которых следует, что при уста­новке порога регистрации сигналов в нуле вероятность сбоя по­сылки и активной паузы резко уменьшается, поскольку эти сигналы разнесены друг от друга на двойную амплитуду принимае­мого сигнала.

 

 

Рис. 10.7

Вероятность сбоя сигнала посылки и активной паузы равна

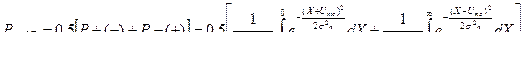.(10.28)

Производя традиционную замену 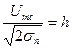, после интегрирования (10.28) находим выражение для вероятности ошибки при приеме сигналов ФТ в отсутствие замираний и действий флуктуационных помех

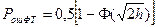.                                            (10.29)

 

Помехоустойчивость фазовой манипуляции при флуктуационных помехах и наличии замираний

 

Для нахождения помехоустойчивости ФТ при наличии зами­раний необходимо учитывать закон распределения амплитуд при­нимаемого сигнала. При рассмотрении .помехоустойчивости AT было показано, что он описывается формулой (10.13).

Учитывая, что закон замирания сигналов ФТ и AT одинаков, поскольку колебание ФТ можно представить двумя колебаниями AT, у которых фаза отличается на π, после соответствующих вы­числений находим вероятность ошибки ФТ при наличии замира­ний

                                       .                (10.30)

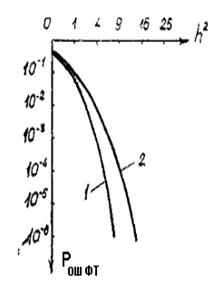
Зависимость вероятности ошибок от отношения сигнал/поме­ха, вычисленных по формулам (10.29) и (10.30), представлены на рис.10.8   кривыми 1 и 2 соответственно.

Рис. 10.8

По сравнению с системами радиосвязи, в которых использу­ются другие виды телеграфии, система с ФТ имеет самую высо­кую помехоустойчивость. Что касается многократной фазовой телеграфии, то ее помехоустой­чивость ухудшается по сравнению с ФТ, так как с ростом кратности уменьшается мини­мальная разность фаз между сигналами.

Как известно, явление «об­ратной работы» исключило при­менение ФТ на практике. На смену ФТ пришла ОФТ, кото­рая, обладая всеми преимущест­вами фазовой телеграфии, свободна от «обратной работы».

Помехоустойчивость ОФТ зависит от способа сравнения по­сылок в приемнике. В главе 1 отмечалось, что такое сравнение может проводиться по высокой частоте (ОФТ-1) или по низкой частоте (ОФТ-2). В [13] показано, что ОФТ-2 обладает помехоустойчи­востью, наиболее близкой к потенциальной.

Так, при переходе от ФТ к ОФТ-2 проигрыш по мощности при вероятности ошибки 10 ^-6не превышает 1,5 дБ. При тех же условиях для ОФТ-1 этот .проигрыш составляет около 2 дБ.

Сказанное выше справедливо при выполнении условий обес­печения высокой стабильности частоты колебаний. Следует пом­нить, что эти требования ужесточаются с ростом рабочей частоты и увеличением скорости телеграфирования.

 

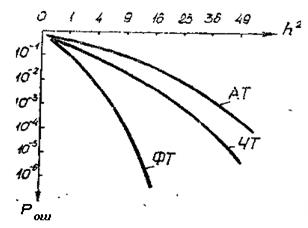
Рис 10.9

В заключение рассмотрим графики зависимости помехоустой­чивости AT, ЧТ и ФТ (рис. 10.9), .построенные по формулам (10.15), (10.22) и (10.30). Из сравнения кривых видно, что помехо­устойчивость ФТ (ОФТ) существенно выше, чем у AT. Относи­тельная фазовая телеграфия, как и ФТ, кроме выигрыша в по­мехоустойчивости позволяет экономно расходовать полосу частот, поскольку 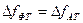. Это обстоятельство является особенно важным тогда, когда при больших скоростях передачи необходи­мо передать максимальное количество информации в ограничен­ной полосе частот. Вот почему в последнее время к ОФТ и другим ее разновидностям проявляется такой большой интерес.

 

10.1.4. ПОМЕХОУСТОЙЧИВОСТЬ СЛОЖНЫХ СИНАЛОВ

При рассмотрении помехоустойчивости AT, ЧТ и ФТ было показано, что вероятность ошибки при приеме элементов сооб­щения зависит от отношения мощности сигнала P_с к мощности шума Р_ш на выходе приемного устройства.

При действии шум с равномерным спектром вместо отношения 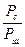вводит пропорциональную ему величину отношения энергии сигнала Е_с за время элементарной посылки Т кспект­ральной плотности шума  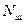[5]

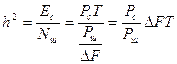                             ,                            (10.31)

где 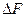 — полоса пропускания приемника, согласованная с ши­риной спектра сигнала.

Произведение 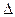FT =В - база сигнала.

Естественно ожидать, что достоверность связи должна увели­чиваться с ростом h². Из формулы (10.31) следует, что увеличить h²можно за счет увеличения либо отношения 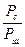, либо  базы сигнала 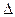FT. Отсюда можно сделать очень интересный вывод, что для ограниченных отношений  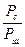  сцелью получения требуемого h² нужно использовать такие виды дискретных сигналов, у ко­торых база 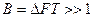. При таком подходе можно осуществить прием сигналов при отношениях 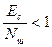. Эту возможность позволяют практически реализовать так называемые сложные сос­тавные сигналы (ССС). Эти сигналы формируются по опреде­ленным правилам, что позволяет статистические свойства ССС сделать близкими к свойствам гауссова шума. Как известно, га­уссов шум имеет почти равномерный энергетический спектр и функцию корреляции в виде узкого основного пика и небольших боковых выбросов. Шумоподобные сигналы такого вида относят­ся к типу широкополосных сигналов (ШПС).

Сложная структура и значительная избыточность ШПС при­дают им многие важные свойства по сравнению с узкополосны­ми сигналами. Применение ШПС в радиосвязи позволило умень­шить влияние многолучевости, ослабить селективные замирания, повысить устойчивость к сосредоточенным и импульсным поме­хам, обеспечить энергетическую скрытность, а также осущест­вить многоадресную передачу информации [3].

Значительный вклад в теорию систем связи с ШПС внесли Л. Е. Варакин, Н. Т. Петрович, М. К. Размахнин, В. Б. Пестряков, Ю. Б. Окунев и др.

Сложные составные сигналы находят широкое применение в дискретных системах радиосвязи. Алгоритм построения ССС поз­воляет даже при базах сигнала, равных тысяче и более, незави­симо формировать их на передающей и приемной стороне, обеспе­чивая при этом жесткую синхронизацию сигналов.

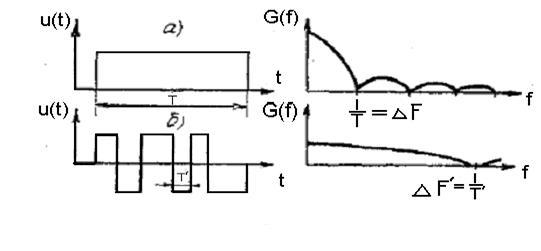
Рис. 10.10

Покажем на примере один из способов формирования ССС, обладающего свойствами шума. Пусть в качестве информацион­ного сигнала выступает посылка длительностью Т (рис. 10.10,а).

 Ширина спектра такого сигнала равна 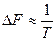,а база .

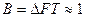Разобьем теперь эту посылку на серию из N бинарных эле­ментов квазислучайной последовательности (рис. 10.10,б). Теперь уже ширина спектра такого сигнала определяется длительностью самого короткого импульса Т¹, а база будет равна .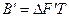

По­скольку 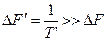,то и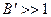

Последовательности бинарных элементов должны обеспечить некоторые заданные свойства сигнала. Для этого используют те или иные коды, на которых остановимся несколько ниже.

Перенос сигнала в область рабочих частот производится с помощью модуляции. Полученный широкополосный сигнал обла­дает рядом новых свойств, которые отсутствовали у исходного уз­кополосного сигнала.

Во-первых, ШПС практически не мешает узкополосным стан­циям, работающим в этом же диапазоне, поскольку уровень ши­рокополосного сигнала ниже уровня помех, так как его мощность распределена в широкой полосе частот.

Во-вторых, сигналы обычных станций не приводят к замет­ным искажениям ШПС, поскольку они при свертке на приемной стороне сами превращаются в ШПС и воспринимаются в виде шума, уровень которого может быть даже ниже уровня естест­венных помех. Кроме того, узкополосные сигналы можно отфильтровать на входе приемника, не причинив особого вреда ШПС.

В-третьих, селективные замирания подавляют ШПС в некото­ром узком диапазоне частот, что не ведет к существенной поте­ре энергии сигнала.

В-четвертых, в ШПС каждый элемент сообщений передается не одним, а многими бинарными элементами, которые несут в се­бе одну и ту же информацию. Чем больше база сигнала, тем больше число бинарных элементов. Созданная таким способом структурная избыточность ШПС позволяет осуществлять накоп­ление сигнала и тем самым реализовать высокую помехоустойчивость даже для случая, когда на входе приемника .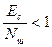

В-пятых, путем выбора соответствующих некоррелированных последовательностей на основе ШПС можно построить многоад­ресную систему радиосвязи, в которой сигналы других абонен­тов будут восприниматься как обычный шум.

При достаточно большом числе N бинарных элементов, пере­даваемых за время информационной посылки, можно прибли­зиться к максимальной пропускной способности канала, опреде­ляемой формулой Шеннона. При этом функция корреля­ции будет иметь главный максимум, сосредоточенный в интер­вале 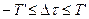и боковые лепестки незначительного уровня (рис. 10.11). Как видно из рисунка, эта функция похожа на функцию автокорреляции гауссова шума. Этим и объясняется название — шумоподобные сигналы.

 

 

Рис 10.11

 

 В то же время сложная структура и расположение последовательностей бинарных элементов в определенном порядке определила и второе название широкополосных сигналов, а именно-сложные составные сигналы (ССС).

 

Известны три способа по­строения ССС на частотно-временной плоскости: последовательный, параллельный и комбинированный [5]. Струк­тура ССС для этих случаев показана на рис. 10.12.

При последовательном способе построения ССС сигнал пред­ставляет собой совокупность элементов длительностью Т_с. Каж­дый элемент может занимать одну и ту же полосу частот (рис. 10.12,а) или передаваться на разных частотах (рис. 10.12,6). Параллельный способ построения ССС основан на од­новременной передаче совокупности элементов несколькими раз­личными частотами (рис. 10.12,в).

 

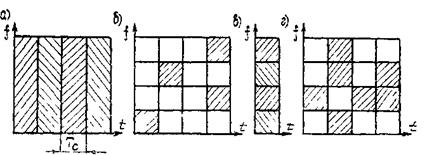
Рис.10.12

В случае комбинированного способа построения ССС все элементы разделяются на две группы, одна из которых передается последовательно во времени на одной частоте, а вторая — одновременно на разных частотах (рис. 10.12,г).

Остановимся более подробно на некоторых видах ССС, ис­пользуемых в радиосвязи.

Последовательные сложные составные сигналы представляют собой N-значные М-последовательности, которые отображают исходную информационную посылку постоянного тока. Они и явля­ются модулирующими сигналами генераторов высоких частот. По­скольку длительность последовательности равна длительности Т_с исходного информационного сигнала, то полоса частот ССС будет равна

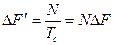,                                                 (10.32)

где 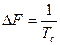— полоса частот  узкополосного информационного сигнала.

 Совершенно очевидно, что и база ССС 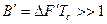. В качестве M-последовательностей чаще всего применяются линейные рекуррентные последовательности, которые обладают хорошими корреляционными свойствами, и их относительно лег­ко реализовать. Несмотря на регулярный способ формирования ССС их структура имеет случайный характер, что и придает им свойства шума. Наибольший интерес представляют собой псевдо­случайные последовательности Хаффмена, которые обладают рядом замечательных свойств. В частности, нормированная функ­ция автокорреляции в непрерывном режиме работы имеет глав­ный максимум, равный единице, и боковые лепестки одинакового уровня, равные — 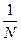. Функция взаимной корреляции для раз­личных последовательностей равна — 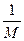. Кроме того, различные М-последовательности при заданном числе знаков отличаются как порядком чередования элементов, так и максимальным значе­нием боковых лепестков.

Наряду с сигналами Хаффмена на практике широко приме­няются сигналы Пэли-Плоткина, коды Баркера, многофазные коды Фрэнка, последовательности символов Лежандра и др.

Применение последовательностей упрощает формирование и прием ССС с помощью регистров сдвига, а также их синхро­низацию.

Последовательные ССС могут составляться из элементов оди­наковой частоты. Для отличия их друг от друга применяется манипуляция фазы частоты элементов исходным информационным сигналом в виде М-последовательности или кодов Баркера, Фрэнка и т. п. Сигналы такого типа имеют хорошие корреляци­онные свойства, что позволяет вести эффективную борьбу с сос­редоточенными помехами, осуществлять селекцию лучей в много­лучевых каналах и обеспечивать скрытность связи.

Последовательные сложные составные сигналы могут форми­роваться из элементов различных частот, которые заданы час­тотно-временной матрицей. В этом случае расстановка частот во времени производится в соответствии с выбранной М-последовательностью. Такие ССС применяются для уплотнения каналов в многоадресных системах радиосвязи.

Кроме последовательных CСC можно сформировать парал­лельные ССС с элементами различных частот [5]. Эти сигна­лы составляются из элементов, образующих множество ортого­нальных функций, на интервале времени, равном Т_с , сисполь­зованием полиномов Эрмита, ортогональных гармонических колебаний и т. п. Такие ССС используются для борьбы с многолучевостью и селективными замираниями.

Практическое применение в последние годы находят ССС с линейным изменением частоты внутри импульса (ЛЧМ). В таких ССС частота прямоугольного импульса длительностью Т_сиз­меняется по линейному закону

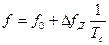                           ,                                          (10.33)

где 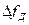 — девиация частоты.

Спектр сигнала ЛЧМ сосредото­чен в полосе частот 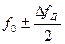.При этом он определяется значе­нием базы В= 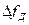Т_с. Область концентрации мощности таких сигналов смещается во времени вдоль оси частот. Эти сигналы также име­ют хорошие корреляционные свойства. Прием сигналов ЛЧМ осуществляется с помощью согласованных фильтров.

Применение ССС не исключает ни одного известного спосо­ба модуляции. Как и в случае узкополосных сигналов, при AM из­меняются амплитуда бинарных элементов ССС, при ЧМ — средняя частота следования элементов, а при ФТ — разность фаз между соседними элементами.

Кроме перечисленных видов модуляции, в системах, исполь­зующих ССС, может еще применяться свойственный только им вид модуляции — структурная модуляция или модуляция по форме сигнала. Примером таких сигналов могут служить про­тивоположные и ортогональные сигналы вида 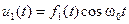и 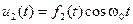. Здесь функции f ₁ ( t ) и f ₂ ( t ) в соответствии с М-последовательностью должны принимать значения ±1 и удовлетворять условию ортогональности .

 Отметим, что техника передачи дискретных со­общений давно вышла за пределы передачи только сигналов теле­графии. Наиболее перспективные системы передачи непрерывных сообщений основываются на преобразовании их посредством квантования в дискретные сигналы. Поэтому системы радиосвя­зи с применением сложных составных сигналов позволяют пере­давать практически все виды дискретной и непрерывной ин­формации.

Применение ССС обеспечивает эффективную борьбу с флуктуационными, сосредоточенными и импульсными помехами. Каза­лось бы, что расширение спектра ССС должно привести к воз­растанию мощности помех в полосе сигнала и к повышению взаимных помех от соседних по спектру сигналов. Однако это не так, поскольку по отношению к ССС применяется опти­мальный прием.

Рассмотрим действие флуктуационных помех на ССС. Извест­но [5], что в случае оптимального приема дискретных сигналов, передаваемых по каналам с гауссовыми шумами, помехоустой­чивость зависит только от отношения энергии сигнала Е_с к спектральной плотности шума N _ш , а от ширины спектра сиг­нала не зависит. Отсюда следует, что помехоустойчивость как узкополосных, так и широкополосных систем одинакова. Прием ССС, как правило, производится на фильтр, согласованный с его широкополосным спектром в полосе ΔF. Если принять коэф­фициент передачи фильтра равным единице во всей полосе ΔF, то отношение мощностей сигнала и шума на выходе согласованно­го фильтра будет равно

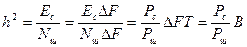                             (10.34)

Полученное выражение совпадает с (10.34). Оно показывает, что при приеме ССС на согласованный фильтр выигрыш на его выходе по сравнению со входом в отношении 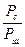   возрастает в В раз. Ранее уже отмечалось, что ССС обладает струк­турной избыточностью. Это позволяет так же, как при синхрон­ном накоплении, в результате обработки ССС и шума в согла­сованном фильтре все N бинарных элементов сигнала, численно равных базе сигналов В, сложить по напряжению, а шумы — по мощности.

Если кроме Р_ш в полосе согласованного фильтра 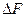 действу­ет еще и сосредоточенная помеха мощностью P_{п ,} например от узкополосной радиостанции или специально организованная, то

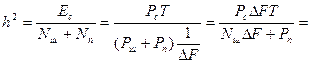
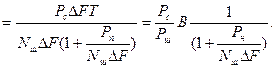           (10.35)

Из (10.35) видно, что при Р_n = const мешающее действие сос­редоточенной помехи обратно пропорционально полосе частот 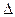F . С сосредоточенной помехой невозможно будет бороться лишь в том случае, если отношение  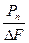с ростом 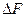остается постоян­ным. Это может случиться только тогда, когда с увеличением 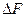будет пропорционально расти мощность помехи. Понятно, что такой вид помехи может быть лишь специально организованной помехой. Однако при достаточно широкой полосе частот может потребоваться настолько большая Р_п, что ее невозможно бу­дет обеспечить. С другой стороны, при приеме сосредоточенной помехи она будет преобразована по закону опорного ССС, в результате чего произойдет распределение энергии сосредото­ченной помехи в широкой полосе частот. Поэтому спектральная плотность помехи понизится, а мощность помехи на выходе при­емника будет определяться только той частью ее спектра, ко­торая проходит через фильтр. Таким образом, сложные состав­ные сигналы более помехоустойчивы к сосредоточенным и спе­циально организованным помехам, чем узкополосные сигналы.

Помехи же от ССС для узкополосных систем подобны флуктуационным шумам и их влияние обратно пропорционально отношению 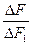, где 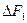— ширина спектра узкополосного сигна­ла. Этим определяется возможность совместной работы широко­полосных и узкополосных систем радиосвязи, если только в их рабочем диапазоне соблюдается регламентация частот для каж­дой радиостанции.

Широкополосные сигналы имеют сравнительно малую спект­ральную плотность, а при некоторых значениях базы сигнала она может стать ниже спектральной мощности шумов. Это откры­вает возможность вести скрытую передачу ССС в рабочем диа­пазоне узкополосных станций и практически не оказывать им мешающего действия.

И, наконец, рассмотрим вопрос о взаимном влиянии между сложными составными сигналами. Будем полагать, что в рабо­чем диапазоне 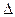F_P передаются п полностью перекрывающихся по спектру широкополосных сигналов, каждый мощностью P_с. Здесь любой сигнал от соседней станции будет восприниматься как помеха. В соответствии с (10.34) отношение сигнал/помеха на выходе согласованного фильтра будет определяться соотношени­ем

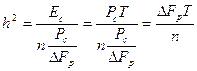.                        (10.36)

Эта формула соответствует случаю, когда все ССС никак не коррелированы между собой. В этом случае несмотря на то, что спектры всех ССС полностью перекрываются, всегда можно со­ответствующим выбором длительности сигнала Т получить тре­буемое превышение его над уровнем сигналов соседних широко­полосных станций. Взаимные же помехи от соседних станций бу­дут действовать как шум, некогерентный с опорным сигналом.

При большом числе широкополосных станций отдельные эле­менты ССС уже могут стать когерентными с опорным сигналом той или иной станции, что приведет к возрастанию помех со сто­роны соседних широкополосных станций.

Вопросы применения широкополосных сигналов для борьбы с мультипликативными помехами в многолучевых каналах радио­связи рассматриваются в [5].

 

10.2. НЕПРЕРЫВНЫЕ СИСТЕМЫ РАДИОСВЯЗИ

Отношение мощности сигнала Р_с к мощности помехи Р_п в канале радиосвязи может быть улучшено приемником. При этом степень улучшения существенно зависит от вида модуляции.

При выборе определенного вида модуляции в той или иной системе радиосвязи прежде всего учитывается получаемая поме­хоустойчивость радиосвязи и ширина полосы частот, занимаемая сигналом в радиоканале. При этом целесообразность выбора то­го или иного вида модуляции оценивается ожидаемой эффектив­ностью канала связи. Как уже отмечалось в главе 7, под эффективностью понимается степень использования полосы частот при заданном отношении мощностей сигнала Р_с и помехи Р_п на вы­ходе приемника.

Анализ процесса детектирования показывает [7], что отношение 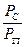на выходе линейного детектора связано с величиной отношения  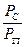на его входе соотношением

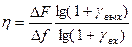^,                               (10.37)

где 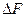 — полоса частот модулирующего сигнала;                                 

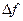 — полоса частот модулированного сигнала;

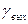— отношение  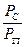на выходе приемника;

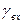  — отношение 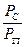на входе приемника.

Выбор вида модуляции зависит от назначения системы ра­диосвязи и условий ее эксплуатации. При этом важнейшим пока­зателем канала радиосвязи выступает требуемая помехоустойчи­вость, которая характеризует степень соответствия принятого со­общения переданному при заданном уровне и характере помех.

В непрерывных системах радиосвязи в качестве меры точнос­ти воспроизведения сообщения на приемном конце принимают величину 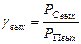, которая в первую очередь зависит от вида модуляции и способа обработки сигнала.

Для удобства сравнения различных систем радиосвязи и оцен­ки их помехоустойчивости часто пользуются величиной

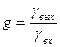                                      (10.38)

или величиной обобщенного выигрыша системы

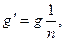                                     (10.39)

где 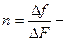 отношение полос пропускания на входе и выхо­де приемника.

Для наглядности (10.39) представим в виде

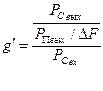.                                (10.40)

Выражение (10.40) раскрывает физический смысл обобщенного выигрыша системы. Он показывает, во сколько раз увеличива­ется отношение мощности сигнала к средней спектральной плот­ности помех на выходе приемника по отношению к мощности сигнала, отнесенной к спектральной плотности помех на входе приемника.

При сравнении различных видов модуляции необходимо знать вид помех, характерный для данной системы радиосвязи.

В диапазоне KB определяющими являются помехи от других систем радиосвязи. Для диапазона УКВ наиболее характерными являются флуктуационные помехи.

Исходя из этого, рассмотрим некоторые виды модуляции с точки зрения величины обобщенного выигрыша системы.

---

Дата добавления: 2019-07-15; просмотров: 642; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!