Помехоустойчивость амплитудной манипуляции при флуктуационных помехах и отсутствие замирания сигналов
Сигнал AT, изображенный на рис. 1.12.бпредставляет собой колебания вида
; (10.2)
u0(t)=0.
Для упрощения задачи вероятность появления u1( t ) и u 0 ( t ) будем считать равной, т. е. p1=р0=0,5.
Вследствие действия на вход приемника сигнала и помехи регистрация как посылки, так и паузы может производиться с ошибкой. Если обозначить вероятность ошибки в регистрации посылки через р+( - ),а вероятность ошибки в регистрации паузы через р - (+), то полная вероятность ошибочного приема будет равна
. (10.3)
Принцип регистрации сигналов AT (рис. 10.1) состоит в том. что если огибающая продетектированного колебания превысит порог U0, то регистрируется посылка, а если окажется ниже порога, то регистрируется пауза.
Рис. 10.1
В паузах на входе приемника действует только флуктуационная помеха с нормальным законом распределения вероятностей. После детектирования плотность вероятности огибающей этой флуктуационной помехи описывается законом Релея
, (10.4)
где Uп— огибающая помехи;
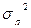— дисперсия помехи.
Плотность вероятности огибающей суммы гармонического сигнала и флуктуационной помехи описывается обобщенным законом Релея
|
|
|
, (10.5)
где U m с — амплитуда гармонического сигнала;
— функция Бесселя первого рода нулевого порядка от мнимого аргумента.
На рис. 10.2 представлены плотности вероятности W ( Un ) и W ( Uсп) для различных отношений сигнала Um с к помехе 
.
Случаи 
соответствует отсутствию сигнала, при котором кривая описывается выражением (10.4).
Выше уже отмечалось, что огибающая на выходе детектора с определенной вероятностью может принимать то или иное положительные значения, а значит, могут появляться ошибки в регистрации посылок и пауз относительно выбранного порога U0 (рис. 10.1).
Полная вероятность ошибочного приема символа будет равна
. (10.6)
В выражении (10.6) первому интегралу соответствует площадь под кривой W ( Uсп) при определенном отношении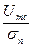 
слева от выбранного порога регистрации u0, а второму интегралу — площадь под кривой W (Uп)справа от U0. Например, для кривой 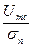= 0 и кривой 4 на рис. 10.2 это соответственно зачерненная и заштрихованная площади.
Рис. 10.2
Превышения порогового уровня 
напряжением помехи Uп (заштрихованная площадь) оценивается вероятностью ложной тревоги Pлт. Если сигнал Uсп окажется ниже порога (зачерненная площадь), то этот случай оценивается вероятностью пропуска цели Рпц. Увеличение мощности сигнала смещает кривую Uсп вправо и вероятность пропуска цели уменьшается при неизменном пороге . Кроме того, увеличивая порог ограничения , можно уменьшить и вероятность ложной тревоги.
|
|
|
Таким образом, величина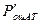 
зависит от установленного порога регистрации U 0 .
подставляя в (10.6) формулы (10.4) и (10.5), получим
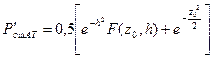, (10.7)
где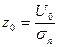 
- отношение порога ограничения к эффективному напряжению помехи;
F ( z0, h ) — функция Райса.
Из формулы (10.7) видно, что вероятность ошибки зависит только от отношения 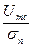и 
. Другими словами, при заданном уровне помех ошибки при регистрации сигналов AT зависят только от выбранного порога регистрации U0и величины напряжения сигнала Um с на выходе приемного устройства. При заданном же отношении 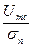вероятность ошибки зависит только от порога регистрации.
Оптимальный порог U0опт , прикотором 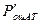будет минимальной, соответствует точке пересечения кривых W ( Uп) и W ( Uсп) приведенных на рис. 10.2.
Исследование на минимум выражения (10.7) приводит к следующему результату
. (10.8)
|
|
|
Решение этого трансцендентного уравнения графически представлено на рис. 10.3.
Рис. 10.3
При больших значениях h , т. е. при малых помехах, справедливо приближенное равенство
, (10.9)
что соответствует оптимальному порогу регистрации сигналов AT, равному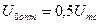 
.
Для малых значений h 
, а оптимальный порог
. (10.10)
Таким образом, для получения минимального значения 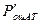, что соответствует максимальной помехоустойчивости, система радиосвязи с AT должна иметь возможность автоматического регулирования порога регистрации, которая в зависимости от отношения сигнал/помеха изменяла бы не только абсолютное значение порога 
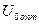, но и его относительную величину 
.
Решить эту задачу довольно сложно, поэтому в системах радиосвязи AT порог регистрации не оптимален, что и является причиной низкой помехоустойчивости амплитудного телеграфирования. При автоматическом приеме на регистрирующую аппаратуру изменение оптимального порога регистрации сигналов AT необходимо производить при 
. При значениях 
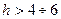оптимальный порог регистрации может быть установлен постоянным
U0опт=0,5Umc . (10.11)
|
|
|
При слуховом приеме сигналов AT удовлетворительные данные могут быть получены при отношении сигнал/помеха 
.
В системах радиосвязи AT для получения максимального отношения сигнала к помехе необходимо полосу пропускания приемного устройства выбирать оптимальной, приблизительно равной 
[4]. При определении минимально возможной полосы пропускания следует учитывать стабильность частоты передатчика и гетеродина приемника, а также требование к форме импульсов с точки зрения обеспечения нормальной работы выходного устройства. При узкой полосе пропускания форма импульсов отличается от прямоугольной, что ухудшает работу оконечных телеграфных устройств. Поэтому для сохранения формы импульсов, близкой к прямоугольной, полосу пропускания приемника выбирают в 3—5 раз шире оптимальной полосы с точки зрения наименьшей вероятности ошибки при приеме сигналов AT.
Дата добавления: 2019-07-15; просмотров: 392; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!