Область пространства, существенная для РРВ. Зоны Френеля.
Каждая точка волнового фронта является источником вторичных волн. Точечный источник формирует сферическую волну, это волну можно разбить на точечные вторичные излучатели которые формируют свою сферическую волну, и если в момент времени 2 аппроксимируем их максимум получим следующую сферическую волну. Т.е. любую волну можно представить в виде вторичных источников, это значит что свет распространяется прямолинейно.(Гюйгенс)
Френель доработал принцип Гюйгенса с точки зрения количественных характеристик.
(П - вектор Герца)
Рассмотрим объем, ограниченный поверхностью, имеется некоторая точка A(точка наблюдения), токи в объеме отсутствуют. Проведем поверхность S за точкой наблюдения, получим некоторую волновую поверхность. Плотность потока мощности мб посчитана как сумма всех источников.
Рис. 2
Можно непосредственно посчитать мощность через вектор герца. (1 выражение сумма вторичных источников (Кирхгоф), 2- сумма непосредственных источников(Герц))
Формула Кирхгофа - математическое обоснование принципа Гюйгенса-Френеля.
Зона существенная для распространения:
Рис. 3
Обосновал Френель. Он разбил поверхность между передатчиком и приемником на зоны.
Рис. 4
Расстояния он выбрал таким образом, чтобы фазы отличались на 
. Это можно записать:
(1)
Фаза при переходе от одной зоны к другой:
(2)
Область существенная для распространения радиоволн будет определятся 1й зоной Френеля. Если мы разобьем 1ю зону Френеля на элементарные отрезки, мы будем иметь знакопеременный ряд:
|
|
|
(3)
Преобразовав и устремив n к бесконечности получим:
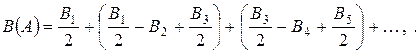(4)
Величина 
будет стремиться к середине 1й зоны Френеля.
Рис. 5
Область существенная для распространения радиоволн содержит в 1ю зону Френеля и некоторые ближайшие участки. (1яона представляет собой круг, а остальные, концентрические кольца)
Рассчитаем размеры зон Френеля:
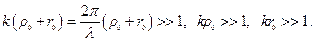(много больше 1, потому что дальняя зона)
Рассмотрим 
:
Отсюда размеры 1й зоны Френеля:
Размер n-й зоны:
Площадь 1й зоны определяется:
Если поверхность S передвинем ближе к приемному концу. Пространственные зоны Френеля представляют собой эллипс:
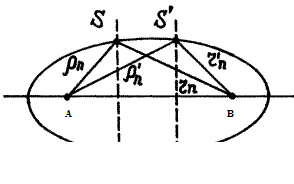
Рис. 6
Уравнение эллипса, с фокусами в точке A и B.
Размеры зон определяются:
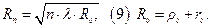
Амплитуда поля за препятствием.
Влияние препятствия(экрана) на распространение, зависит от его расположения относительно области существенной для распространения радиоволн.
Из рис. 8, поле в точке A существенно не изменится, зато в точке A1 оно существенно ослабляется препятствием. В данном случае влияние экрана на распределения поля носит название дифракции(возмущения поля за препятствием). Амплитуда поля за экраном зависит от того какие зоны Френеля оказываются закрыты экраном. При закрытии периферийных зон Френеля амплитуда поля осциллирует, т.е. то уменьшается если открыто четное число зон Френеля, то увеличивается, если отрыто нечетное число зон. Амплитуда поля осцилляции увеличивается по мере приближения экрана к ближним зонам Френеля. При перекрытии ближних зон Френеля и подходе к 1й зоне(область II), амплитуда поля за экраном максимальная, т.е. влияние полностью открытой 1й зоны Френеля практически не компенсируется полями перекрытых остальных зон, по мере перекрытия 1 зоны(область III и IV), амплитуда поля монотонно убывает, поскольку вклад этой зоны в дифракцию является определяющим.
|
|
|
Рис. 9
Рис. 10
Дата добавления: 2019-07-15; просмотров: 315; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!