Назначение, устройство, принцип действия и классификация зеркальных антенн Основные геометрические соотношения и параметры параболических зеркал.

Очень широкое распространение получили зеркальные антенны. Формирует довольно узкую ДН. Обеспечивает фокусирование электромагнитной энергии, в качестве облучателя обычно используются рупорные антенны.

 

 

Существует множество видов зеркальных антенн наибольшее распространение получили антенны в виде зеркала параболоида вращения(справа) либо параболического цилиндра(слева)

Если необходимо создать ДН веерной формы используют вырезки из параболоида вращения(слева).

Для того чтобы сформировать ДН специального вида(косеконсную) для дальномера, она формируется за счет кривизны зеркала.

 

 

С развитием науки начали использовать многозеркальные антенны. Спутниковые системы делают двузеркальные. Система Грегори.

Система Кассегрена

 

 

Параболическая антенна:

Есть возможность формирования многолучевой ДН:

 

Перископическая антенна, нет необходимости тянуть волноводный тракт, на верхнее зеркало(г). В виде полу развернутой книжки, но набольшее распространение получили зеркальные антенны.

 

Основные геометрические соотношения параболических зеркал.

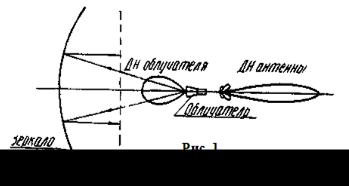
Из всех типов зеркал наилучшим фокусирующими свойствами. Парабола является геометрическим местом точек равноудаленных от некоторой прямой (директрисой) и точки фокуса несовпадающей с этой прямой. Изобразим параболу

 

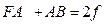
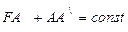
Из определения параболы слндует ее основное свойство: Сумма расстояний от фокуса ф до произвольной точки А и от точки а до точки А` на раскрыве величина постоянная. Благодаря этому оптические пути от фокуса до точек раскрыва оказываются одинаковыми, и сферическая волна, создаваемая облучателем, помещенным в фокус, после отражения от параболоида вращения превращается в плоскую.

-ДН излучателя.

F – точка фокуса

О – вершина зеркала

FO – оптическая ось

Z­₀ – глубина зеркала

f_0­­(θ) –ДН облучателя

2θ₀ – угол раскрыва зеркала

a–радиус зеркала

 

 

Решаем апертурным методом:

Исходя из определения параболы:

Для того, чтобы путь ээммаг волны от облучателя к плоскости зеркала обратно к плоскости апертуры путь был одинаков, для этого зеркало искривляется специальным образом:

 

подставим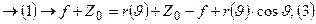

Решим относительно:

(4) уравнение параболы в полярной системы координат, с фокусом в точке F.

 

В прямоугольной системе координат:

где p это параметр(расстояние от точки фокуса до директрисы параболы): из рисунка 5б: - позволяет определить один из геометрических размеров параболы(если известны 2 других).

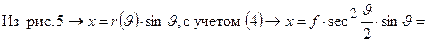путем элементарных преобразований

В плоскости апертуры:

- характеризует количественно и качественно глубину зеркала. При 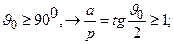-глубокие зеркала.Мелкие зеркала -

---

Дата добавления: 2019-07-15; просмотров: 380; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!