Множитель системы прямоугольно раскрыва с разделяющимся амплитудно-фазовым распределением.
Размер по горизонтали
(от -a/2 до a/2) , размер по горизонтали. Вертикальный размер (от -b/2 до b/2). Остальное аналогично рис 2.
Рассмотрим ДН плоского прямоугольного раскрыва в плоскости XOY. Размер узкой стенки определим величиной (b), узкой (a). Определить множитель системы. Данная постановка задачи не ограничивает общности рассуждения поскольку ось OX выбрана произвольно.
Учтем что: 
Следовательно:
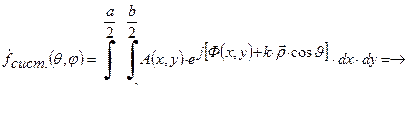
и учтем что 
Замечание: множитель системы излучателей расположенных в плоскости (7) представляет собой двумерной преобразование Фурье амплитудно-фазового распределения(АФР) в раскрыве, поэтому множитель системы является двумерной функцией с ограниченным спектром.
В (7) первый интеграл зависит от X, второй от Y. Здесь вводится в рассмотрение разделяющееся АФР. Практически для всех антенн СВЧ УКВ диапазона можно считать АФР разделяющееся. При разделяющемся АФР:
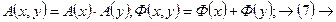
Множитель системы для прямоугольного излучающего раскрыва представляет собой произведение двух независимых сомножителей каждый из которых зависит от одной координаты X и Y. Полученные соотношения позволяют рассмотреть ДН прямоугольного излучающего раскрыва.
Множитель системы в главных плоскостях.
Рассмотрим ДН прямоугольного раскрыва в главных плоскостях:
(вдоль оси X)
Множитель системы в плоскости H запишем:
Т.к. множитель системы в плоскости не зависит от координаты Y, то второй интеграл константа, то:
|
|
|
Аналогично для плоскости E:
Полученные выражения (10) и (11) с точностью до постоянного множителя, совпадает с рассмотренной множителем системы для линейной системы излучателей. Из этих выражений следует, что при разделяющихся АФР ДН прямоугольного раскрыва в главных плоскостях сводится к ДН линейных антенн, соответственно вдоль координатных осей X и Y.(т.е. можно рассматривать линейку излучателей вдоль осей при разделяющихся АФР)
Все выводы полученные для линейных систем излучателей справедливы и здесь:
«Н»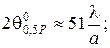 
(12) «Е» 
(13) 
Можно управлять ДН в плоскостях X и Y.(по азимуту и углу места).
При сканировании нарушение симметричности, за счет уменьшения действующей длины:
ДН с точки зрения сканирующих антенн:
Круглый излучающий раскрыв.
Рассмотрим круглый излучающий раскрыв. Поместим
начало координат в центр раскрыва и выразим амплитудно-фазовое распределение через полярные координаты раскрыва и подставим их в выражение (3).
Наиболее часто используются синфазные раскрывы с амплитудным распределением, не зависящим от радиуса 
также введем некоторые обозначения, получим:
Используя представление для функции Бесселя нулевого порядка:
|
|
|
Как это следует из физических соображений, множитель системы от 
не зависит, является вещественной функцией. Последнее означает, что раскрыв излучает сферическую волну. Фазовый центр находится в центре антенны. В случае равномерного амплитудного распределения:
При: 
Нормированная ДН:
Ширина ДН, уровень боковых лепестков, КНД, и коэффициент использования поверхности:
Таким образом, видно, что при переходе от прямоугольно раскрыва к круглому приводит снижению уровня боковых лепестков и расширению главного лепестка.
Дата добавления: 2019-07-15; просмотров: 340; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!