Понятие о дискретной системе излучателей. Поле системы излучателей. Теорема перемножения диаграммы направленности антенны (ДНА).
Пусть имеется некоторая дискретная система (набор дискретных излучателей) расположенных произвольным образом в пространстве. Определить поле в точке Р.
В законы электродинамики все параметры входят в первой степени, значит они линейны, следовательно, принцип суперпозиции применим. Разобьем антенну на элементарные излучатели, тогда поле в точке Р.
Поле центрального излучателя:
Соответственно поле i-го излучателя:
Комплексная векторная ДН определяется:
Т.к. источники идентичны то и их ДН идентичны:
Т.о. поле в точке наблюдения можно записать:
А так как поле мы рассматриваем в дальней зоне, то 
(справа из прошлой темы). 
Проанализируем выражение(6) преобразованное с учетом (5) и (7):
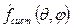-множитель системы.
Правило перемножения диаграмм(правило Бонч-Бруевича)
Проведем математические преобразования:
(8) 
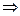
- амплитудное распределения в системе токов или полей. 
-фазовое распределение токов или полей.
Мы можем записать:
Соответственно:
Отсюда и вытекает правило перемножения диаграмм. Если нам необходимо определить ДН системы дискретных излучателей мы должны взять ДН центрального излучателя и умножить на множитель системы. Условия применения: идентичные излучатели, одинаково ориентированы, одна поляризация.
Физический смысл множителя системы - состоит в том, что он описывает пространственную, интерференционную картину излучения(комплексную ДН), системы изотропных излучателей с тем же амплитудно-фазовым распределением что и в антенне.
|
|
|
Графическая интерпретация правила перемножения диаграмм.
Результирующая ДН изображена пунктиром.
В основном ДН определяет множитель системы.
При перемножении не должно быть чтобы макс множителя системы совпадал, с мин ДН центрального излучения.
Понятие об амплитудном и фазовом распределении. Множитель линейной дискретной системы с равномерным амплитудным и линейным фазовым распределением.
Множитель системы линейной дискретной системы с равномерным амплитудным и линейным фазовым распределением.
Рассмотрим модель из двух излучателей. Дальняя зона. Внизу справа критерии дальней зоны.
Из определения cos:
Подставим в (9)
Равномерное амплитудное распределение, =1.
Линейное фазовое распределение(N- количество излучателей в системе)
С учетом количества излучателей:
А с учетом обозначении(14) и =1:
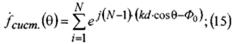
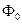-начальная фаза. Обозначим 
Используем формулу геометрической прогрессии. 
Выполнив преобразования:
-фазовое распределение в системе(фазовая диаграмма решетки).
В общем случае нас интересует модуль:
Вводится обобщенны угол 
следовательно множитель системы преобразуется( 
- обобщенный угол):
|
|
|
Анализ множителя линейной дискретной системы. Направление главных максимумов и ширина ДН. Условие единственности главного максимума. Направление нулевого излучения и боковые лепестки. Коэффициент направленного действия.
Дата добавления: 2019-07-15; просмотров: 609; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!