Линейная непрерывная система излучателей с равномерным амплитудным и линейным фазовым распределением.
Рассмотри обычный симметричный вибратор.

Разобьем на элементарные излучающие участки. Чтобы определить поле в дальней зоне
 ДН определим по правилу перемножения диаграмм, множитель системы запишем как у дискретной системы излучателей.
ДН определим по правилу перемножения диаграмм, множитель системы запишем как у дискретной системы излучателей.


Из дискретной получим непрерывную систем, рассмотрев предельное соотношение(аналогично для фазового и амплитудного распределения):


(5)Множитель непрерывной системы излучателей для любого амплитудного и фазового распределения.
Множитель системы синфазной и равномерно возбужденной антенны.

 (преобразование по формулам Эйлера)
(преобразование по формулам Эйлера)
 - Нормированный множитель системы)
- Нормированный множитель системы)
Из графика видно что ноли ДН определяются:  Направление и уровень БЛ определяются соответственно:
Направление и уровень БЛ определяются соответственно: 
Ширина ДН определяется по уровню половинной мощности из условия:
 или решая это трансцидентное уравнение и пользуя таблицей
или решая это трансцидентное уравнение и пользуя таблицей  , получим
, получим  перейдя к реальным углам
перейдя к реальным углам  , а поскольку L>>
, а поскольку L>> 


Множитель системы синфазной линейной антенны с симметричным амплитудным распределением.


Вычислим интеграл (16) с учетом  и нормируя получим:
и нормируя получим:
 график на рис.3. Анализируя амплитудное и косинусоидальное распределения мы видим: произошло расширение гл. луча ДН и уменьшение уровня БЛ.
график на рис.3. Анализируя амплитудное и косинусоидальное распределения мы видим: произошло расширение гл. луча ДН и уменьшение уровня БЛ.
Решая это трансцидентное уравнение и пользуя таблицей  , получим:
, получим: 
В общем виде амплитудное распределение можно представить в виде:


Пример:
|
|
|
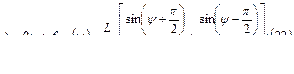
Нормированный множитель системы:

Таблица №1

Существует еще биномиальная ДН, ее характеристики гораздо лучше, чем у приведенных в таблице 1, но реализовать на техники ее на технике не удалось. Активно используется оптимальное амплитудное распределение (Дольф-Чебышевское), сочетает и узкую ДН и приемлемых уровень БЛ.
При косинусоидальном распределении мы можем антенну разбить, на множество элементарных антенн с равномерным амплитудным распределением, одна антенна короче другой, то ширина ДН будет увеличиваться, в связи с уменьшение действующей длины антенны, уровень бок лепестков будет уменьшаться.

 Ниже построим множитель системы(1 соответствует 1, n-n), для самой длинной антенны самая узкая ДН и самый высокий уровень, для самой короткой антенны наоборот. В итоге боковые лепестки компенсируют друг друга, в результате при косинусоидальном распределений получаем небольшой уровень БЛ.
Ниже построим множитель системы(1 соответствует 1, n-n), для самой длинной антенны самая узкая ДН и самый высокий уровень, для самой короткой антенны наоборот. В итоге боковые лепестки компенсируют друг друга, в результате при косинусоидальном распределений получаем небольшой уровень БЛ.
Сравнительный анализ множителей системы с различными амплитудно-фазовыми распределениями (АФР).
Рассмотрим линейное фазовое распределение:
Фазовое распределение представим в виде степенного ряда:
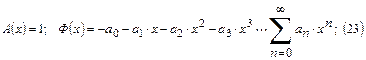
 Квадратичное и кубичное фазовое распределение используется редко, обычно используется, линейное.
Квадратичное и кубичное фазовое распределение используется редко, обычно используется, линейное.
|
|
|
Рассмотрим множитель системы, подставим 

Антенна от 1 до -1, линейное фазовое распределение 
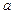 - определяет скорость нарастания. Множитель системы в обобщенных углах, сдвинут на величину
- определяет скорость нарастания. Множитель системы в обобщенных углах, сдвинут на величину 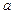 .
.

 Отсюда:
Отсюда:


 Множитель системы в обобщенных углах сдвинулся, в полярных координатах, сместившись на величину
Множитель системы в обобщенных углах сдвинулся, в полярных координатах, сместившись на величину 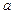 опустим перпендикуляр, то увидим, что действующая длина уменьшилась, следовательно будет расширяться гл. луч ДН, нарушение симметрии, расширяться, будет больше в ту сторону в которую отклоняется данный луч. Что отражено и в реальных углах на рис. 9
опустим перпендикуляр, то увидим, что действующая длина уменьшилась, следовательно будет расширяться гл. луч ДН, нарушение симметрии, расширяться, будет больше в ту сторону в которую отклоняется данный луч. Что отражено и в реальных углах на рис. 9

Т.о, мы видим что обобщенных углах нет нарушения симметрии, а в реальных есть.
(Рис 10а)- вращаем без сканирования получается тор, а если будем вращать со сканирующим лучом(Рис 10а) то будем наблюдать свертывание ДН в форму воронки, это снижает точность определения координат.
 Система излучателей, расположенных в плоскости.
Система излучателей, расположенных в плоскости.
Большинство антенн характеризуется излучателями, расположенными в плоскости.
Рассмотрим систему излучателей расположенных в плоскости, элементарная излучающая площадка dS(источник Гюйгенса).
Определим множитель системы. Применим теорему перемножения диаграмм.
|
|
|

Так площадь произвольная то множитель системы:  учтем что:
учтем что: 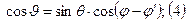
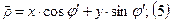 Тогда ДН:
Тогда ДН: 
 -площадь раскрыва антенны.
-площадь раскрыва антенны.
Дата добавления: 2019-07-15; просмотров: 822; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
