N-процеси домінують за наявності резистивних процесів

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

У цьому граничному випадку передбачається, що розподіл фононів встановлюється тільки за рахунок N-процесів, а розсіяння на дефектах не міняє цього розподілу. У варіаційний вираз N-процеси, таким чином, не дають внеску. Для даного виду (q) знаменник виразу можна записати в простій формі. Через те що

Знаменник має вигляд

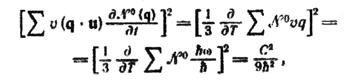
де величина |u| прийнята рівною 1, оскільки u² міститься і в чисельнику, і в знаменнику. Коли має місце ізотропне розсіяння і вірогідність P (q, q') залежить тільки від відносної орієнтації q та q', чисельник також набуває простій вигляд, і, замінюючи суму інтегруванням, його можна записати у такому вигляді

Тепловий опір тоді визначається формулою

яка співпадає з виразом Каллуея в тій же межі переважання N-процесів.

Слід відмітити, що якщо τ(q) ~ q^-4, як у разі точкових дефектів, то й вираз для теплопровідності залишається кінцевим, оскільки інтеграл має

Вигляд

і сходиться на обох межах. Якщо розсіяння менш сильно залежить від q, наприклад τ(q) ~ q^-1, то простий релаксаційний метод дає кінцеву теплопровідність; збільшення часу релаксації із зменшенням q не врівноважує зменшення внеску цих мод в теплопровідність, яка визначається енергією фононів і щільністю станів, пропорційною q². Вираз для ϰ, отриманий простим релаксаційним методом, містить тоді

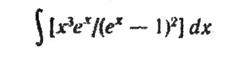
тоді як варіаційний вираз або формула Каллуея при домінуванні N-процесів містить

Всі ці інтеграли досягають граничних значень при дуже малих х, і відношення χ_рел/χ_N_дом стає рівним 1,3. Як видно, резистивне розсіяння все ще грає важливу роль для малих значень q, але внесок від домінуючих N-процесів сильно не збільшує теплового опору.

Метод Гюйе і Крумхансла

Серед методів, заснованих на використанні рівняння Больцмана для фононів, заслуговує уваги робота Гюйе і Крумхансла по гідродинаміці фононів. Вона є порівняно раннім дослідженням загальних властивостей фононних систем. Передбачається, що розподіл фононів залежить від часу і координат. Зміна розподілу по ширині кристала, а також і уздовж його довжини при постійному температурному градієнті приводить до пуазейльовського протікання, тоді як зміна розподілу з часом дозволяє отримати другий звук, який є хвилевим процесом розповсюдження зміни N.

Розгляд ведеться з використанням операторної форми для рівняння Больцмана, і загальні результати виражаються через оператори зіткнень, причому розрізняються оператори для нормального розсіяння N* і для резистивного розсіяння R*. Вирішення рівняння Больцмана і, отже, виразу для потоку тепла і теплопровідності записуються через цих операторів, тому необхідно тільки виразити останні через швидкості релаксації і , щоб довести відповіді до числових результатів.

За умови N* > R*, відповідному >> , теплопровідність виходить та ж, що і визначувана другим членом виразу Каллуея; отже, вона співпадає з величиною, знайденою варіаційним методом при переважанні N-процесів. За умови R* > N*, відповідному >> , виходить той же вираз для теплопровідності, що і при простому релаксаційному методі; тут вона також співпадає з першим членом у виразі Каллуея.

Гюйе і Крумхансл приводять вираз, справедливий для всього інтервалу відносних значень і :

(4.3.1)

де

а 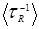– таке ж середнє для [τ_R(х)]^-1. Величина S рівна / 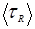і називається чинником перемикання. Якщо << , тo величина S велика і в дужках виразу (3.3.1) найбільш важливий член . Peзистивні процеси тоді переважають, і теплопровідність виходить така ж, як при використанні простого релаксаційного методу. У разі τ_R >> τ_N величина S мала і головну роль грає член ^-¹. Нормальні процеси визначають розподіли фононів, і вираз для теплопровідності співпадає з формулою Займана і Каллуея для цього граничного випадку, а тепловий опір аддитивний.

У проміжній області відносних значень τ_R і τ_N швидкості розсіяння, що отримуються при аналізі експериментів за допомогою виразів Каллуея і Гюйе – Крумхансла, дуже близькі, але погодження дещо гірше, якщо ≈ ^-1.

Висновки

Одним з ефектів, що обумовлений ангармонічним характером коливань атомів, є тепловий опір твердих тіл. Він не міг б виникнути, якби атоми здійснювали строго гармонійні коливання, що розповсюджуються в решітках у вигляді системи пружних хвиль, що не взаємодіють між собою. Відсутність взаємодії між хвилями дозволяла б їм розповсюджуватися в кристалі не розсіваючись, тобто не зустрічаючи ніякого опору, подібно до розповсюдження світла в порожнечі.

Якби в такому кристалі можна було створити різницю температур, то атоми гарячого кінця, що коливаються з великими амплітудами, передавали б свою енергію сусіднім атомам і фронт теплової хвилі розповсюджувався б уздовж кристала із швидкістю звуку. Оскільки ця хвиля не зустрічала б ніякого опору, то навіть при нескінченно малій різниці температур тепловий потік міг би досягати якої завгодно великої величини; теплопровідність такого кристала була б нескінченно великою.

У реальних кристалах при не дуже низьких температурах коливання атомів носять ангармонічний характер. Поява ангармонічності призводить до того, що нормальні коливання решіток втрачають незалежний характер і при зустрічах взаємодіють один з одним, обмінюючись енергією і змінюючи напрям свого розповсюдження (розсіваючись один на одному). Саме внаслідок протікання таких процесів взаємодії пружних хвиль стає можливою передача енергії від коливань однієї частоти до коливань іншої частоти і встановлення в кристалі теплової рівноваги.

Опис процесу розсіяння нормальних коливань один на одному зручно вести на мові фононів, розглядаючи термічно збуджений кристал як ящик, заповнений фононами. У гармонійному наближенні, в якому нормальні коливання решіток є незалежними, фонони утворюють ідеальний газ (газ невзаємодіючих фононів). Перехід до ангармонічних коливань еквівалентний введенню взаємодії між фононами, в результаті якої можуть відбуватися процеси розщеплювання фонона на два і більш і утворення одного фонона з двох. Такі процеси прийнято називати фонон-фононним розсіянням.

Всі процеси розсіяння, внаслідок якого розподіл фононів прагне до рівноважного, прямо впливають на теплопровідність. Для більшості процесів інтенсивність розсіяння залежить від частоти фононів, і N-процеси грають важливу роль, перерозподіляючи енергію між різними модами і тим самим перешкоджаючи сильному відхиленню від рівноважної населеності в кожній моді. Взагалі кажучи, важко виділити внесок від N-процесів, і необхідний досить докладний аналіз експериментальних результатів, щоб зрозуміти, як позначаються N-процеси на теплопровідності. Проте у ряді випадків їх вплив дуже істотний.

Дата добавления: 2019-07-15; просмотров: 184; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 Следующая ⇒

Мы поможем в написании ваших работ!