Випадок переважання резистивного розсіяння
Для кристала з великою кількістю дефектів всі моди сильно розсіваються унаслідок резистивних процесів; тоді для всіх мод τN >> τR , отже, τC ≈ τR. У такому разі ϰ2 << ϰ1 (якісно це можна зрозуміти, припустивши, що всі часи релаксації не залежать від частоти, тому при порівнянні ϰ1 та ϰ2 інтеграли скорочуються і ми маємо ϰ2/ ϰ1 = τR/τN << 1). Пізніше буде видно, що це порівняльно простий вираз придатний для аналізу експериментальних даних по теплопровідності не дуже ідеальних кристалів.
Випадок переважання N-процесів за наявності резистивного розсіяння
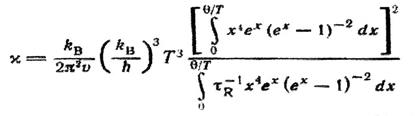
В цьому випадку час релаксації τC головним чином визначається N-процесами; тоді τR >> τN і τC ≈ τN. Звідси легко побачити, що ϰ2 >> ϰ1 (якісно це можна зрозуміти, припустивши незалежність часів релаксації від частоти, і отримати ϰ/ϰ1 = τR/τN >> 1). Для коефіцієнта теплопровідності тоді маємо
Перш за все дивно, що формула (4.1.2), яка визначає теплопровідність у разі переважання N-процесів, не містить τN. Проте N-процеси впливають на розподіл фононів і приводять його до форми (3.1). Коли N-процеси грають домінуючу роль, розподіл фононів стає «зміщеним» і не залежить від інтенсивності N-процесів. Тепловий опір виникає внаслідок резистивних процесів, що діють на цей розподіл.
Інший цікавий аспект формули (4.1.2) видно, якщо з її допомогою записати тепловий опір:
|
|
|
(4.1.3)
Для певного кристала при заданій температурі знаменник виразу (4.1.3) постійний. Оскільки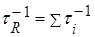 
– сума швидкостей розсіяння для всіх типів резистивних процесів, то видно, що 
, де Wi – тепловий опір, відповідний кожному резистивному процесу i, що діє окремо, але за умови переважання N-процесів. У загальному випадку тепловий опір неаддитивний, оскільки у формулі для ϰ1 швидкості релаксації складаються в знаменнику інтеграла (комбінований релаксаційний час міститься в чисельнику), а, крім того (за винятком розглянутого тут граничного випадку), формула для ϰ2 дуже складна і не приводить до такого простого результату.
Представляючи функції від ϰ, що входять в (4.1.3), через С(ϰ) і повну теплоємність С і проводячи прості арифметичні дії, запишемо вираз (4.1.3) у вигляді
(4.1.4.а)
Слід порівняти вираз (4.1.4.а) з виразом для теплопровідності, отриманим релаксаційним методом у відсутність N-процесів. В цьому випадку час релаксації кожної моди множиться на її внесок в теплоємність, а потім інтегрується по всіх модах для отримання теплопровідності. Якщо ж переважають N-процеси, то швидкість релаксації кожної моди множиться на її внесок в теплоємність і після інтеграції виходить повний тепловий опір. В останньому випадку квадрат теплоємності в знаменнику виразу (4.1.4.а) приводить до теплового опору, зворотного теплоємності, і до теплопровідності, пропорційній першому ступеню теплоємності.
|
|
|
Оскільки υτ = l. можна у вираз (4.1.4.а) ввести середню довжину вільного пробігу:
(4.1.4.б)
Варіаційний метод у разі переважання N-процесів дає той же результат, тобто вирази (4.1.4.а) і (4.1.4.б).
Існує серія експериментів, в яких досліджувався вплив дефектів, причому для пояснення їх можна прямо застосувати розглянуту тут теорію.
У одному випадку метод Каллуея не знаходить застосування. Якщо резистивне розсіяння має місце тільки на межах кристала, а N-процеси відбуваються достатньо часто, то у виразі (4.1.4.а) не можна представляти значення υ/D для 
(D – відповідний лінійний розмір кристала). Якщо проте це зробити, то отримаємо
Останній вираз представляє якраз опір внаслідок розсіяння на межах у відсутність N-процесів, а отже, виходить, що N-процеси в даному випадку не грають ніякої ролі. Насправді для цієї спеціальної комбінації розсіяння теплопровідність перевищує величину теплопровідності, отриману при розсіянні на межах у відсутність N-процесів, в число разів, рівне швидкості релаксації для N-процесів.
|
|
|
Дата добавления: 2019-07-15; просмотров: 177; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!