Симметричные двойственные задачи

Разновидностью двойственных задач линейного , программирования являются двойственные симметричные задачи, в ко­торых система ограничений как исходной, так и двойственной задач задается неравенствами, причем на двойст­венные переменные налагается условие неотрицательности.

Исходная задача. Найти матрицу-столбец Х = (x₁, x₂, …, x_n), которая удовлетворяет системе ограничений

(1.12).                АХ>А₀, Х>0

и минимизирует линейную функцию Z = СХ.

Двойственная задача. Найти матрицу-строку Y = (y₁, y₂, …, y_n), которая удовлетворяет системе ограничений YA £ C, Y ³ 0 и максимизирует линейную функцию f = YA ₀.

Систему неравенств с помощью дополнительных переменных мож­но преобразовать в систему уравнений, поэтому всякую пару симмет­ричных двойственных задач можно преобразовать в пару несимметрич­ных, для которых теорема двойственности уже доказана.

Используя симметричность, можно выбрать задачу, более удоб­ную для решения. Объем задачи, решаемой с помощью ЭВМ, ограни­чен числом включаемых строк, поэтому задача, довольно громоздкая в исходной постановке, может быть упрощена в двойственной формули­ровке. При вычислениях без помощи машин использование двойствен­ности упрощает вычисления.

Исходная задача. Найти минимальное значение линейной функции Z = x₁ + 2x₂ + 3x₃ при ограничениях

 

 2x₁ + 2x₂ - x₃ ³ 2,

x₁ - x₂ - 4x₃ £ -3,       x_i ³ 0 (i=1,2,3)

x₁ + x₂ - 2x₃ ³ 6,

 2x₁ + x₂ - 2x₃ ³ 3,

Очевидно, для того чтобы записать двойственную задачу, сначала необходимо систему ограничений исходной задачи привести к виду (1.12). Для этого второе неравенство следует умножить на -1.

Двойственная задача. Найти максимум линейной функции f = 2y₁+ 3y₂ + 6y₃ + 3y₄ при ограничениях

2y₁ - y₂ + y₃ + 2y₄ £ 1,

2y₁ + y₂ + y₃ + y₄ ³ 2,

 -y₁+ 4y₂ - 2y₃ - 2y₄ ³ 3,

Для решения исходной задачи необходимо ввести четыре дополни­тельные переменные и после преобразования системы - одну искус­ственную. Таким образом, исходная симплексная таблица будет состо­ять из шести строк и девяти столбцов, элементы которых подлежат преобразованию.

Для решения двойственной задачи необходимо ввести три допол­нительные переменные. Система ограничений не требует предваритель­ных преобразований, ее первая симплексная таблица содержит четыре строки и восемь столбцов.

Двойственную задачу решаем симплексным методом (табл. 1.3).

Оптимальный план двойственной задачи Y* = (0; 1/2; 3/2; 0), f_max = 21/2.

Оптимальный план исходной задачи находим, используя оценки (m + 1)-й строки последней итерации, стоящие в столбцах A₅, A₆, A₇ : x₁ = 3/2 + 0 = 3/2; x₂ = 9/2 + 0 = 9/2; x₃= 0+ 0 = 0. При оптимальном плане исходной задачи X* = (3/2; 9/2; 0) линейная функ­ция достигает наименьшего значения: Z_min =21/2.

Т а б л и ц а 1.3

i	Базис	С базиса	A0	2				3		6			3		0		0		0
				A1				A2		A3			A4		A5		A6		A7
1 2 3	A5 A3 A7	0 0 0	1 2 3	2 2 -1				-1 1 4		1 1 -2			2 -1 -2		1 0 0		0 1 0		0 0 1
m + 1	Zi - Cj		0	-2				-3		-6			-3		0		0		0
1 2 3	A3 A6 A7	6 0 0	1 1 5	2 0 3				-1 2 6		1 0 0			2 -1 2		1 -1 2		0 1 0		0 0 1
m + 1	Zi - Cj		6		10		-9				0		9		6		0		0
1 2 3	A3 A2 A7	6 3 0	3/2 ½ 2			2 0 3			0 1 0			1 0 0		3/2 -1/2 4		½ -1/2 5		½ ½ 3	0 0 1
m + 1	Zi - Cj		21/2			10			0			0		9/2		3/2		9/2	0

 

Виды математических моделей двойственных задач

На основании рассмотренных несимметричных и симметричных двойственных задач можно заключить, что математические модели пары двойственных задач могут иметь один из следующих видов.

Н е с и м м е т р и ч н ы е з а д а ч и

(1) Исходная задача       Двойственная задача

    Z_min = CX;                     f_max = YA₀;

       AX = A₀;                     YA £ С .

        X ³ 0.

(2) Исходная задача       Двойственная задача

      Z_max = CX;                     f_min = YA₀;

       AX = A₀;                       YA ³ С .

        X ³ 0.

С и м м е т р и ч н ы е з а д а ч и

(3) Исходная задача       Двойственная задача

      Z_min = CX;                     f_max = YA₀;

       AX ³ A₀;                       YA £ С .

        X ³ 0.                            Y ³ 0.

 (4) Исходная задача        Двойственная задача

      Z_max = CX;                     f_min = YA₀;

       AX £ A₀;                       YA ³ С .

        X ³ 0.                            Y ³ 0.

Таким образом, прежде чем записать двойственную задачу для данной исходной, систему ограничений исходной задачи необходимо привести к соответствующему виду. Запишем, например, математиче­скую модель двойственной задачи для следующей исходной.

Найти минимальное значение линейной функции Z = 2x₁ + x₂ + 5x₃ при ограничениях

 

 

x₁ – x₂ – x₃ £ 4,

x₁ – 5x₂ + x₃ ³ 5,             x_j ³ 0 (j = 1, 2, 3).

2x₁ – x₂ + 3x₃ ³6,

Рассматриваемая задача относится к симметричным двойственным задачам на отыскание минимального значения линейной функции. Для того чтобы было можно записать двойственную задачу, ее модель долж­на иметь вид (3). Переход осуществляется умножением первого не­равенства на -1.

Исходная задача:

Z_min = 2x₁ + x₂ + 5x₃ при ограничениях

-x₁ + x₂ + x₃ ³ -4,

x₁ – 5x₂ + x₃ ³ 5,             x_j ³ 0 (j = 1, 2, 3).

2x₁ – x₂ + 3x₃ ³6,

Двойственная задача:

f_min = -4x₁ + 5x₂ + 6x₃ при ограничениях

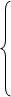-y₁ + y₂ + 2y₃ £ 2,

y₁ – 5y₂ - y₃ £ 1,             y_i ³ 0 (i = 1, 2, 3).

2y₁ + y₂ + 3y₃ £ 5,

Приведем без доказательства следующую теорему. Теорема 1.1. Если при подстановке компонент оптимального пла­на в систему ограничений исходной задачи i-e ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи равна нулю.

Если i-я компонента оптимального плана двойственной задачи по­ложительна, то i-e ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.

---

Дата добавления: 2019-07-15; просмотров: 181; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!