Временное и спектральное представление дискретизированного сигнала
Дельта - импульс (единичный импульс) – математическая абстракция, амплитуда которого равна нулю при любых значениях времени, кроме t=0. В природе его не существует, но он широко используется для моделирования реальных сигналов. Дельта - импульс должен удовлетворять двум условиям:
Δt =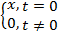 
=1
Рис.3. Временная диаграмма одиночного импульса
Рис.4. Спектр одиночного дельта импульса
Рис.5. Временная диаграмма периодической последовательности дельта-импульсов
Так как сигнал периодический, то его спектр будет дискретным. Спектр периодической последовательности - импульсов представлен на рис. 6.
Рис.6. Спектр периодической последовательности дельта-импульсов
Рис.7. Спектр исходного непрерывного сигнала.
Спектр дискретного сигнала состоит из суммы спектров исходного непрерывного сигнала, сдвинутых друг относительно друга по оси частот на величину равную частоте дискретизации ωд
Рис.7. Спектр дискретизированного сигнала.
Реально при дискретизации располагают не последовательностью дельта-импульсов, а последовательностью импульсов конечной длительности.
В результате процесса дискретизации получают не последовательность дельта-импульсов, амплитуда которых соответствует значению непрерывного сигнала в тактовые моменты времени, а последовательность реальных, например, прямоугольных импульсов, амплитуда которых соответствует значениям непрерывного сигнала в тактовые моменты времени.
|
|
|
Рис.8. Временные диаграммы аналогового сигнала, периодической
последовательности импульсов и дискретизированного сигнала
Спектр дискретизированного сигнала импульсами конечной длительности, похож на спектр дискретизированного сигнала при дискретизации дельта-импульсами, но амплитуда составляющих спектра убывает с ростом номера гармоники.
Рис.9. Спектр дискретизированного сигнала импульсами
конечной длительности
Процесс квантования
Полученный, после дискретизации, АИМ-сигнал является аналоговым, поскольку амплитуда импульсов изменяется в соответствии с амплитудой непрерывного сигнала и может принимать бесконечное множество значений. Поэтому помехоустойчивость АИМ-сигнала не превышает помехоустойчивости исходного аналогового сигнала.
Для преобразования АИМ-сигнала в цифровой производится квантование сигнала по уровню мощности и последующее кодирование квантованных отсчетов. Обобщенно данные операции называют аналого-цифровым преобразованием.
При квантовании по уровню диапазон возможных значений сигнала делится на отрезки, называемые шагами квантования. Внутри каждого шага выбирают разрешенные значения сигнала – уровни квантования.
|
|
|
Рис.10. Квантование и шум квантования
Амплитуда каждого отсчета Uаим(t) округляется до значения ближайшего уровня квантования и отсчету присваивается значение величины разрешенного уровня Uкв(t). Амплитуды квантованных импульсов отличаются от амплитуды отчетов, что приводит к искажению сигнала, а на приемном конце возникают помехи, которые называют шумом квантования. Шум квантования представляет собой последовательность импульсов следующих с частотой дискретизации и имеющих случайную амплитуду.
Ошибка квантования может быть определена как
(t) = 
В зависимости от того, изменяется ли шаг квантования в области значений сигнала, процесс квантования называют равномерным (линейным) или неравномерным (нелинейным).
Равномерным (линейным) называется квантование, если шаг квантования (∆) остается постоянным в допустимых пределах возможных значений.
Амплитудная характеристика имеет два характерных участка: зону квантования и зону ограничения. Если входной АИМ – сигнал удовлетворяет условиям (-U0)≤ Uвх≤ U0, то он попадает в зону квантования. Если это условие не удовлетворяется, то сигнал попадает в зону ограничения. В результате произойдет ограничение максимального значения сигнала, и ему будет присвоено значение Uогр.
|
|
|
Ограничение мгновенных значений сигнала приводит к появлению шумов ограничения. Средняя мощность шума квантования: Рш.кв.=∆2/12, где ∆- шаг квантования.
Максимальное число уровней квантования:
М =(2Uмах /∆) + 1= (2Uогр. /∆) + 1
Необходимое число уровней при равномерном квантовании М=512…2048.
Рис.11. Амплитудная характеристика квантующего устройства
Uвых=f(Uвх) с равномерным шагом квантования
Недостатком равномерного квантования является то, что относительная ошибка шума квантования велика для слабых сигналов и уменьшается с возрастанием уровня квантования.
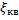– абсолютная ошибка шума квантования;
γкв – относительная ошибка шума квантования.
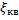γкв= /Uкв
Устранить недостатки равномерного квантования можно, используя неравномерное (нелинейное) квантование.
Неравномерным(нелинейным) называется квантование, если шаг квантования изменяется в допустимых пределах амплитудных значений, возрастая с увеличением уровня сигнала.
Относительная ошибка шума квантования будет практически постоянна на всем диапазоне изменения входного сигнала.
|
|
|
Неравномерное квантование позволяет сократить число шагов квантования. Для обеспечения требуемого качества при равномерном квантовании необходимо М = 2048, что соответствует m=11 (разрядность код.группы), а при неравномерном квантовании для тех же показателей М=128, m=7, следовательно, существенно упрощается аппаратура.
Рис.11. Амплитудная характеристика квантующего устройства
с неравномерным шагом квантования
4. Процесс кодирования.
При переходе от аналоговых к цифровым сетям связи возникла необходимость преобразовать аналоговый электрический сигнал в цифровой формат на передающей стороне, то есть закодировать, и затем после приема перевести обратно в аналоговую форму, то есть декодировать.
Цель любой схемы кодирования - получить такую цифровую последовательность, которая требует минимальной скорости передачи и из которой декодер может восстановить исходный речевой сигнал с минимальными искажениями.
Как указывалось выше, при преобразовании речевого сигнала в цифровую форму, так или иначе имеют место два процесса – дискретизация и квантование. Указанные два шага (дискретизация и квантование) определяют процессы, осуществляемые приимпульсно-кодовой модуляции (ИКМ). Они позволяют перейти от аналогового представления речевого сигнала к цифровому.
Для сигнала с ограниченным спектром, к которому относится и сигнал стандартного телефонного канала (0,3 – 3,4) кГц, имеющего частоту среза fcp = 4 кГц, применима теорема Котельникова-Найквиста, определяющая fд = 2 fcр. Отсюда получаем, что для стандартного телефонного канала частота дискретизации составляете 8 кГц(т.е. выборки аналогового сигнала следуют с периодом дискретизации Тд = 125 мкс).
Численное значение каждой выборки в этой схеме может быть далее представлено (закодировано) в виде 7 или 8 битного двоичного кода (на практике при использовании аналого-цифровых преобразователей (АЦП), двоичное кодирование осуществляется непосредственно при квантовании). Такое кодирование (часто называемое кодификацией) дает возможность передать 128 (27) или 256 (28) дискретных уровней амплитуды речевого сигнала, обеспечивая качественную передачу речи формально с динамическим диапазоном порядка 42 или 48 дБ. Учитывая, что выборки должны передаваться последовательно, получаем двоичный цифровой поток со скоростью 56 кбит/с (8 кГц х 7 бит) в случае 7 битного кодирования или 64 кбит/с (8 кГц х 8 бит) в случае 8 битного кодирования.
Рис.12. Формирование двоичного потока при ИКМ
с 7 – битным кодированием
Дата добавления: 2019-07-15; просмотров: 605; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!