Временное и спектральное представление ФМ сигнала.

    Фазовой модуляцией называется процесс изменения мгновенного значения фазы высокочастотного несущего колебания по закону низкочастотного информационного сигнала (сообщения), оставляя при этом неизменной амплитуду его колебаний. Для простоты анализа рассмотрим модуляцию гармоническим колебанием одной частоты Ω, изменяющейся по закону косинуса т.е.

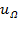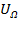= cosΩt

При фазовой модуляции сигналом одного тона, получить выражение для тока при ФМ не сложно. Обычный немодулированный сигнал представляется следующим выражением iа=I_mcos(wt+j₀),где j₀– начальная фаза, определяемая выбором начала отсчёта времени. Этот сигнал получает дополнительный фазовый сдвиг ΔjcosWt, который изменяется по закону модулирующего сигнала. Тогда уравнение модулированного по фазе тока принимает следующий вид: iа=I_mcos(wt+j₀+ΔjcosWt).Приняв j₀ = 0, получим

iа=I_mcos(wt+ΔjcosWt),где Δφ- величина, характеризующая максимальное отклонение полной фазы колебания от её значения до модуляции.

Максимальная девиация фазы при фазовой модуляции Δj называется индексом фазовой модуляции (Δj пропорционален амплитуде модулирующего напряжения 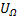и не зависит от его частоты).

График фазово-модулированного колебания приведен на рис.5. из которого видно, что во время положительного полупериода модулирующего напряжения фазово-модулированное колебание опережает по фазе колебание несущей частоты.

 

Рис.5. График фазово-модулированного колебания

 

Из графика видно, что во время положительного полупериода модулирующего напряжения фазовомодулированное колебание опережает по фазе колебание несущей частоты. При этом период колебания радиочастоты уменьшается, а частота возрастает. В отрицательный полупериод модулирующего напряжения фазовомодулированное колебание отстаёт по фазе то колебания средней (несущей) частоты. Период его увеличивается, а частота уменьшается.

Таким образом, фазовая модуляция сопровождается частотной. Изменение частоты при фазовой модуляции можно выразить следующим образом:

ω= 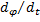 = 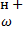ΔjΩsinWt.

       Здесь произведение ΔjΩявляется девиацией частоты при фазовой модуляции. Значение девиации частоты при фазовой модуляции прямо пропорционально амплитуде модулирующего напряжения 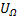 и его частоте Ω.

       Поскольку и при частотной, и при фазовой модуляции происходит изменение фазового угла, то каждую из них называют угловой модуляцией.

    Сравнивая уравнения тока в антенне при фазовой модуляции с таким же уравнением для тока при частотной модуляции, видим, что при модуляции одним тоном частотная и фазовые модуляции оказываются одинаковыми и различить их невозможно.

    Однако при модуляции спектром частот, например при разговоре, частотная и фазовая модуляции существенно отличаются. Это различие в том, что при частотной модуляции приращение частоты радиочастотных колебаний пропорционально только амплитуде модулирующего колебания (силе звука) Δω = К 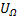 и не зависит от частоты модуляции. А при фазовой модуляции приращение частоты Δω пропорционально не только амплитуде, но частоте модулирующего напряжения 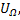т.е. Δω = К .

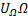    Поэтому при приёме фазовомодулированных колебаний на приёмник с частотным детектором более высокие частоты передаваемого звука будут воспроизведены с большей громкостью, чем низкие. И передача будет искажена.

Установлено, что при фазовой модуляции также как и при частотной модуляции воздействие одной модулирующей частоты дает не две боковые частоты, а бесчисленное множество боковых частот. Эти боковые частоты отстоят друг от друга на величину модулирующей частоты и амплитуды их уменьшаются по мере увеличения частоты.

При определенных условиях спектры ЧМ и ФМ-сигналов могут быть совершенно одинаковыми, как показано на рис. 6, а и в.

Ширина спектра ФМ колебания будет равна Δ 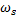≈2 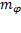+1)Ω или

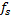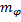Δ ≈2( +1)F.

Однако достаточно измениться, например, частоте модуляции (при неизменной амплитуде управляющего сигнала), чтобы спектры ЧМ- и ФМ-сигналов стали различными. На рис. 6, б показано, как изменяется спектр ЧМ-сигнала при уменьшении вдвое частоты модуляции. При этом соответственно уменьшается интервал между боковыми составляющими, но ширина спектра остается практически неизменной, поскольку индекс модуляции увеличивается вдвое и девиация частоты не меняется.

При этом же изменении частоты модуляции спектр ФМ-сигнала меняется иначе (рис. 6, г). Здесь также соответственно уменьшается интервал между боковыми составляющими, но уменьшается и ширина спектра, так как вдвое уменьшается девиация частоты при неизменном индексе модуляции.

Таким образом, из сравнения рис. 6, б и г видно, что в общем случае спектры ЧМ и ФМ-сигналов отличаются при одном и том же управляющем сигнале. При этом, как видно из рисунка, отличаются не только амплитуды боковых составляющих (за счет разных индексов модуляции), но и их число.

 

Рис.6. Сравнение спектров ЧМ и ФМ сигналов

   Для определения спектрального состава колебания с угловой модуляцией (ЧМ и ФМ) используется выражение :

s(t) =  +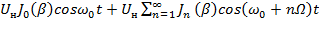

+ ,

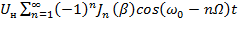где 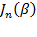 - Бесселева функция первого рода n-го порядка от аргумента β,

в данном случае β – это индекс модуляци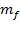и (  или ).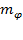

---

Дата добавления: 2019-07-15; просмотров: 942; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!