Этап 4 Спецификация и параметризация
Этап 1 Постановочный
Целью этой работы является изучение взаимозаменяемости продовольственных товаров: масла животного и масла растительного. А затем построение модели, которую можно было бы использовать для прогнозирования взаимозаменяемости товаров.
Этап 2 Априорный
Изучив сложившуюся ситуацию на рынке продовольственных товаров, я пришла к выводу, что взаимозаменяемость вышеуказанных продуктов зависит от цент на эти продукты, от национальных предпочтений, от удаленности от производства, сезонных особенностей употребления этих продуктов.
Итак, результативный признак Y – потребление животного масла кг., фактор Х – потребление растительного масла кг.
Этап 3 Информационный
Для изучения влияния именно фактора Х (потребление растительного масла), постараемся отобрать в выборку однородные участки, т.е. с примерно одинаковыми характеристиками, и за один и тот же период времени.
В выборку отобрано 55 регионов РФ, расположенных в Южном федеральном округе, Приволжском федеральном округе, Уральском федеральном округе, Сибирском федеральном округе и Дальневосточном федеральном округе на январь – февраль 2007 года.
Источник статистических данных – сайт Госкомстата РФ, распечатки прилагаются.
| № | У (потребление животного масла), кг | Х (потребление растительного масла), кг |
| Республика Адыгея | 50,8 | 138,4 |
| Республика Дагестан | 50,8 | 147,5 |
| Республика Ингушетия | 46,3 | 113 |
| Кабардино-Балкарская Республика | 65,1 | 167 |
| Республика Калмыкия | 45,5 | 105,6 |
| Карачаево-Черкесская Республика | 66,9 | 167,2 |
| Республика Северная Осетия - Алания | 76,1 | 198,7 |
| Краснодарский край | 83,1 | 252,1 |
| Ставропольский край | 63,9 | 197 |
| Астраханская область | 108,4 | 217,8 |
| Волгоградская область | 91,5 | 243,1 |
| Ростовская область | 86,5 | 242,1 |
| Республика Башкортостан | 105,6 | 261,3 |
| Республика Марий Эл | 64,4 | 149,4 |
| Республика Мордовия | 59,5 | 151,1 |
| Республика Татарстан | 118,5 | 266,8 |
| № | У (потребление животного масла), кг | Х (потребление растительного масла), кг |
| Удмуртская Республика | 68,1 | 172,7 |
| Чувашская Республика | 55,9 | 149,7 |
| Пермский край | 118,9 | 294,5 |
| Кировская область | 53 | 168,3 |
| Нижегородская область | 80,2 | 227,2 |
| Оренбургская область | 74,4 | 209,6 |
| Пензенская область | 82,8 | 183,8 |
| Самарская область | 85,2 | 237,1 |
| Саратовская область | 90,5 | 190,3 |
| Ульяновская область | 80,3 | 196,7 |
| Курганская область | 68,6 | 194 |
| Свердловская область | 104,2 | 285,1 |
| Тюменская область | 173,3 | 455 |
| Ханты-Мансийский авт.округ-Югра | 221,4 | 547,8 |
| Ямало-Ненецкий авт. округ | 195,9 | 546,1 |
| Челябинская область | 87 | 230,8 |
| Республика Алтай | 63,7 | 154,7 |
| Республика Бурятия | 80,2 | 190,4 |
| Республика Тыва | 41 | 88 |
| Республика Хакасия | 66,9 | 171,8 |
| Алтайский край | 66,4 | 202,9 |
| Забайкальский край | 79,9 | 167,3 |
| Агинский Бурятский авт. округ | 73,2 | 162,8 |
| Красноярский край | 103,2 | 276,9 |
| Иркутская область | 89,5 | 210,3 |
| Усть-Ордынский Бурятский авт. округ | 43,7 | 82,7 |
| Кемеровская область | 93,3 | 258,4 |
| Новосибирская область | 90,5 | 229,9 |
| Омская область | 102,7 | 272,3 |
| Томская область | 107 | 273,5 |
| Республика Саха (Якутия) | 116,6 | 254,6 |
| Камчатский край | 90,8 | 293,2 |
| Приморский край | 73,9 | 208,3 |
| Хабаровский край | 83,5 | 294 |
| Амурская область | 56,4 | 185,2 |
| Магаданская область | 99 | 290,6 |
| Сахалинская область | 113,4 | 372,2 |
| Еврейская автономная область | 65,5 | 174 |
| Чукотский авт. округ | 108,2 | 285,8 |
Предварительный анализ статистических данных
Основные расчёты были проведены с помощью программы MathCAD (распечатки прилагаются).
(Или: Для удобства вычислений в ходе решения будем достраивать исходную таблицу данных до вспомогательной таблицы (см. расчетную таблицу ниже), округляя и занося в неё промежуточные результаты).
Поле корреляции и линия регрессии
Сначала построим поле корреляции – точки с координатами (х i , у i), и по их расположению сформулируем предположение о связи Y(потребление животного масла) и X(потребление растительного масла).

Визуальный анализ полученного поля корреляции показывает, что точки располагаются вдоль некоторой воображаемой возрастающей прямой линии, причём достаточно плотно, слабо рассеиваясь около неё.
Т.е. можно сказать, что прослеживается тесная прямая (положительная) зависимость, т.к. чем больше потребление растительного масла, тем больше потребление животного масла, которое зависит от сезонных особенностей.
Также можно заметить, что варьирование (дисперсия) потребление животного масла сильнее при малом потреблении растительного масла, а при большем потреблении – дисперсия потребления животного масла мала. Следовательно, можно предположить, что в модели будет гетероскедастичность.
Проверим наши предположения аналитически, с помощью расчётов на следующих этапах.
Основные характеристики выборки
Средние значения:  и
и  .
.
Стандартные отклонения:  и
и 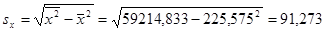
(где  и
и  ).
).
Итак, в данной выборке рассматриваются взаимозаменяемость потребления растительного масла в среднем на 225,275 кг. со стандартным отклонением 91,273 кг., потребления животного масла в среднем составила 86,02 кг. со стандартным отклонением 33,777 кг.
Линейный коэффициент корреляции:

(где  ).
).
Это подтверждает сделанные ранее выводы.
Т.к.  , то взаимозаменяемость животного масла«растительного масла действительно можно считать линейной. Эта линейная зависимость положительна. Теснота связи очень сильная. А значит, линейная парная регрессионная модель вполне подойдёт для исследования и описания взаимозаменяемость животного масла«растительного масла.
, то взаимозаменяемость животного масла«растительного масла действительно можно считать линейной. Эта линейная зависимость положительна. Теснота связи очень сильная. А значит, линейная парная регрессионная модель вполне подойдёт для исследования и описания взаимозаменяемость животного масла«растительного масла.
Этап 4 Спецификация и параметризация
Линейная парная регрессионная модель
На основе предыдущих этапов можем с большой уверенностью предположить, что взаимозаменяемость животного масла и растительного масла – линейна.
Тогда для моделирования используем линейную парную регрессионную модель  для генеральной совокупности.
для генеральной совокупности.
Для выборки модель также линейна:  .
.
Найдём объяснённую часть модели - линейное уравнение регрессии по выборке:  . Для этого нужно найти коэффициенты регрессии а0 и а1, являющиеся оценками параметров a 0 и a1 линейной модели. А затем оценим случайную составляющую e с помощью остатков ei и проверим выполнение для них предпосылок МНК.
. Для этого нужно найти коэффициенты регрессии а0 и а1, являющиеся оценками параметров a 0 и a1 линейной модели. А затем оценим случайную составляющую e с помощью остатков ei и проверим выполнение для них предпосылок МНК.
Этап 5 Идентификация
Для построения модели используем классический подход - метод наименьших квадратов МНК.
Из системы нормальных уравнений:
 находим коэффициенты регрессии а0 и а1.
находим коэффициенты регрессии а0 и а1.
Все необходимые числовые значения рассчитаны ранее (см. расчетную таблицу), подставим их в систему нормальных уравнений:  ему нормальных уравнений: бюджет льуплений от налога на прибыль предприятий о с увеличением размера среднемесячной зарплаты Х н
ему нормальных уравнений: бюджет льуплений от налога на прибыль предприятий о с увеличением размера среднемесячной зарплаты Х н
и решим её относительно а0, а1. Получим коэффициенты регрессии: а0=6,622 и  .
.
Итак, уравнение регрессии имеет вид:  .
.
Коэффициент а0=6,622 формально интерпретируется как взаимозаменяемость потребление животного масла, равным нулю, т.е. при х=0. Это вполне имеет смысл. Т.о., взаимозаменяемость животного масла в среднем в январе – декабре 2007 г. составляла 6,622 кг.
А коэффициент  показывает, что полученная линейная связь взаимозаменяемости потребления животного масла (результативного признака Y) и растительного масла (фактора Х) – положительна, то есть при увеличении потребления растительного масла на 1 кг. от среднего значения, то потребление животного масла вырастит на 0,352 от среднего значения.
показывает, что полученная линейная связь взаимозаменяемости потребления животного масла (результативного признака Y) и растительного масла (фактора Х) – положительна, то есть при увеличении потребления растительного масла на 1 кг. от среднего значения, то потребление животного масла вырастит на 0,352 от среднего значения.
В декартовой системе координат ХОУ на поле корреляции строим и график линии регрессии по найденному уравнению.

Действительно, видим, что точки поля корреляции плотно расположены вдоль прямой регрессии. А значит, построенная линейная модель хорошо описывает стат. данные. Проведём подробный анализ её качества.
Этап 6 Верификация
Линейный коэффициент корреляции
Вычислим егопо другой формуле, проверим правильность расчётов:
 - совпадает с вычисленным ранее (небольшое различие – из-за округления).
- совпадает с вычисленным ранее (небольшое различие – из-за округления).
Коэффициент детерминации
По свойству:  .
.
Он показывает, что вариация результативного признака Y (потребление животного масла) на 90,6% объясняется вариацией фактора X (потребление растительного масла). То есть потребление животного масла на 78,6% обусловлены взаимозаменяемостью растительного масла. А в остальном – на 9,4% потребления животного масла обусловлено колебаниями и изменениями других факторов и условий.
Т.е., подтвердилось предположение о взаимозаменяемости потребления животного масла и растительного масла.
Средний коэффициент эластичности
Для линейной регрессии:  .
.
Средний коэффициент эластичности показывает, что в среднем при увеличении потребления животного масла на 1% от своего среднего значения, потребление растительного масла увеличится в среднем на 0,923% от своего среднего значения.
Эластичность взаимозаменяемых товаров достаточно велика, что вполне согласуется со сложившейся ситуацией на рынке продовольствия в РФ. Чем выше продажа растительного масла, тем сильнее и заметнее растет продажа животного масла. Проверим правильность вычислений:  (см. расчётную табл. - действительно).
(см. расчётную табл. - действительно).
Оценка статистической значимости коэффициентов регрессии и коэффициента корреляции
Оценим статистическую значимость полученных коэффициентов регрессии а0 и а1, коэффициента корреляции r ух с помощью t-критерия Стьюдента на уровне значимости d=0,05.
Эта проверка проводится по единой схеме, с помощью гипотез.
Выдвигается нулевая гипотеза Н0 о случайной природе полученного коэффициента, о незначимом его отличии от нуля, то есть гипотеза Н0 состоит в том, что коэффициент=0. Альтернативная ей гипотеза Н1 состоит в том, что  неслучайно, то есть полученный коэффициент статистически значим. Чтобы опровергнуть гипотезу Н0 и подтвердить гипотезу Н1 должно выполняться неравенство
неслучайно, то есть полученный коэффициент статистически значим. Чтобы опровергнуть гипотезу Н0 и подтвердить гипотезу Н1 должно выполняться неравенство  на уровне значимости
на уровне значимости  и с (n –2) степенями свободы, где n – количество наблюдений, уровень значимости – вероятность совершить ошибку, отвергнув гипотезу Н0, когда она верна.
и с (n –2) степенями свободы, где n – количество наблюдений, уровень значимости – вероятность совершить ошибку, отвергнув гипотезу Н0, когда она верна.
Для а1: Н0: а1=0, Н1:  .
.
Рассчитаем стандартную ошибку коэффициента регрессии а1 –  .
.
Потребуется сделать промежуточные вычисления: подставляя фактические значения х i в уравнение регрессии найдем смоделированные значения  , затем вычислим разность между фактическими и смоделированными значениями, т.е. остатки
, затем вычислим разность между фактическими и смоделированными значениями, т.е. остатки  , затем возведём остатки в квадрат е i 2 и просуммируем; результаты представлены в расчетной таблице. Теперь подставим необходимые данные в формулу для расчёта
, затем возведём остатки в квадрат е i 2 и просуммируем; результаты представлены в расчетной таблице. Теперь подставим необходимые данные в формулу для расчёта  :
:  и t-статистики по модулю:
и t-статистики по модулю:  .
.
Затем сравним наблюдаемое значение  с табличным значением t-критерия Стьюдента. Табличное значение по таблице распределения Стьюдента на уровне значимости d=0,05 с n –2=55-2=53степенями свободы: t табл=2,01. Наблюдаемое значение t-статистики превышает табличное значение t-критерия: 22 > 2,01, то есть выполнено неравенство
с табличным значением t-критерия Стьюдента. Табличное значение по таблице распределения Стьюдента на уровне значимости d=0,05 с n –2=55-2=53степенями свободы: t табл=2,01. Наблюдаемое значение t-статистики превышает табличное значение t-критерия: 22 > 2,01, то есть выполнено неравенство  , а значит, гипотеза Н0 о случайной природе полученного коэффициента отвергается и принимается альтернативная ей гипотеза Н1, свидетельствующая в 95% случаев о статистической значимости полученного коэффициента регрессии а1. Т.о., можно считать, что взаимозаменяемость товаров подтвердилась и статистически установлена.
, а значит, гипотеза Н0 о случайной природе полученного коэффициента отвергается и принимается альтернативная ей гипотеза Н1, свидетельствующая в 95% случаев о статистической значимости полученного коэффициента регрессии а1. Т.о., можно считать, что взаимозаменяемость товаров подтвердилась и статистически установлена.
Для а0: Н0: а0=0, Н1:  .
.
Рассчитаем стандартную ошибку коэффициента регрессии а0 –  . Все необходимые цифры уже имеются в расчетной таблице, подставим эти данные в формулу:
. Все необходимые цифры уже имеются в расчетной таблице, подставим эти данные в формулу:  , а затем рассчитаем t-статистику по модулю:
, а затем рассчитаем t-статистику по модулю:  .
.
Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости d=0,05 с n –2=55-2=53степенями свободы: t табл=2,01,где 2<ta 0< 3 (t табл > ta 0) можно сделать вывод, что коэффициент регрессии а0 можно признать статистически значимым в 90% случаев.
Для r ух: Н0: r ух=0, Н1: 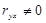 .
.
Для этого рассчитаем стандартную ошибку коэффициента корреляции r ух –  :
:  и t-статистику по модулю:
и t-статистику по модулю:  .
.
Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости d=0,05 с n –2=55-2=53степенями свободы: t табл=2,01, можно сделать вывод о статистической значимости полученного коэффициента корреляции r ух в 95% случаев, предполагаемая взаимозаменяемость товаров подтвердилась.
Проверим правильность вычислений:  , действительно 22»22,7.
, действительно 22»22,7.
Доверительные интервалы для параметров регрессионной модели a 0 и a 1
Доверительный интервал для a 0 с надежностью g=1-d:  . Выбрав уровень значимости d=0,05, получаем надежность g=0,95. Все необходимые цифровые значения уже рассчитаны ранее, тогда
. Выбрав уровень значимости d=0,05, получаем надежность g=0,95. Все необходимые цифровые значения уже рассчитаны ранее, тогда  , откуда получаем (0,4312; 12,813).ыберемрительной вероятностью ров регрессионной модели XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
, откуда получаем (0,4312; 12,813).ыберемрительной вероятностью ров регрессионной модели XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Доверительный интервал для a 1 с надежностью g=1-d:  . При выбранной надежности g=0,95:
. При выбранной надежности g=0,95:  , откуда (0,32; 0,384).
, откуда (0,32; 0,384).
Таким образом, с надежностью 95% можно утверждать, что истинное значение параметра a 0 будет заключено в пределах от 0,4312 до 12,813, а истинное значение параметра a 1 - в границах от 0,32 до 0,384.
Следует отметить, что доверительные интервалы узкие, т.к. значения стандартных ошибок  и
и  малы. А это подтверждает, что другие факторы оказывают несущественное влияние на покупательскую способность товаров. Основным фактором является выбранный фактор Х – замена растительным маслом. Значит, точность модели будет вполне приемлемой.
малы. А это подтверждает, что другие факторы оказывают несущественное влияние на покупательскую способность товаров. Основным фактором является выбранный фактор Х – замена растительным маслом. Значит, точность модели будет вполне приемлемой.
Оценка качества уравнения регрессии в целом
F -критерий Фишера
Выдвигается нулевая гипотеза Н0 о статистической незначимости уравнения регрессии. Альтернативная ей гипотеза Н1 о статистической значимости. Чтобы опровергнуть гипотезу Н0 и подтвердить гипотезу Н1 должно выполняться неравенство  .
.
Рассчитаем наблюдаемое значение F-критерия (воспользуемся свойством для линейной парной регрессии):  .
.
Табличное значение по таблице распределения Фишера на уровне значимости d=0,05 с k 1=1 и k 2=n –2=23-2=21степенями свободы: F табл=4,03. Наблюдаемое значение F–критерия превышает табличное: 510,83 > 4,03, то есть выполнено неравенство  , а значит, гипотеза Н0 о случайной природе полученного уравнения регрессии отклоняется в пользу гипотезы Н1, свидетельствующей в 95% случаев о его статистической значимости и взаимозаменяемости товаров. Уравнение по данным выборки можно признать надежным и значимым, доказывающим наличие исследуемой зависимости.
, а значит, гипотеза Н0 о случайной природе полученного уравнения регрессии отклоняется в пользу гипотезы Н1, свидетельствующей в 95% случаев о его статистической значимости и взаимозаменяемости товаров. Уравнение по данным выборки можно признать надежным и значимым, доказывающим наличие исследуемой зависимости.
Оценка аппроксимации модели
Потребуется сделать промежуточные вычисления: остатки е i разделим на фактические значения у i, полученные частные от этих делений возьмем по модулю  и просуммируем; результаты представлены в расчетной таблице.
и просуммируем; результаты представлены в расчетной таблице.
Средние ошибки аппроксимации:  ,
,  . Ошибки почти совпадают и равны »25%.
. Ошибки почти совпадают и равны »25%.
В среднем смоделированные значения взаимозаменяемость животного масла отклоняются от фактических на 9-12%. Подбор модели к фактическим данным можно оценить как не точный, так как средняя ошибка аппроксимации превышает 20%.
Но, учитывая высокое качество модели и сильную линейную зависимость между Y (потребление животного масла) и Х (потребление растительного масла), эту модель можно использовать для прогнозирования с осторожностью.
Т.к. большую погрешность. Только при этом следует помнить, что в некоторых случаях прогнозы могут быть вполне точны, а в некоторых содержать немаленькую погрешность, до 12% в среднем.
Дата добавления: 2019-07-15; просмотров: 130; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
