Свойства делимости в целых полугруппах

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

(1) ;

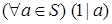(2) – рефлексивность;

(3) – антисимметричность;

(4) – транзитивность;

(5) ;

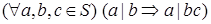(6) ;

(7) Любой простой элемент неприводим;

(8) р неприводим Û ;

Свойство 1. НОД и НОК нескольких элементов определены однозначно, если существуют.

Доказательство. Проведем доказательство для НОД двух элементов а и b из S. Пусть (a,b) и (a,b). Тогда из определения НОД следует и . По свойству антисимметричности имеем .

Свойство 2. .

Доказательство. Импликации и очевидны. Пусть , т.е. для некоторого . Очевидно, b – общий делитель а и b. Возьмем произвольный общий делитель с элементов а и b. Для него существуют такой элемент , что и . Таким образом, с делит b. Это и означает, что . Аналогично доказывается .

Следствие 1. .

Следствие 2. и .

Свойство 3. и .

Доказательство следует из коммутативности операции умножения и свойств делимости.

Свойство 4. .

Доказательство. Обозначим d₁=НОД(НОД(a , b), c). Так как d₁ является общим делителем НОД(a , b)и c, то d₁ – общий делитель и для элементов a , b и c. Верно и обратно: любой общий делитель этих трех элементов является общим делителем для НОД(a , b)и c. Аналогичным свойством обладает и элемент d₂=НОД(a , (НОД(b , c)). Тогда элементы d₁ и d₂ делят друг друга. По свойству антисимметричности делимости получаем d₁=d₂.

Свойство 5. .

Доказательство. Обозначим k₁=НОК(НОК(a , b), c). Так как k₁является общим кратным элементов НОК(a , b)и c, то k₁ – общее кратное и для элементов a , b и c. Верно и обратно: любое общее кратное этих трех элементов является общим кратным для НОК(a , b)и c. Аналогичным свойством обладает и элемент k₂=НОК(НОК(a , b), c). Тогда элементы k₁и k₂ делят друг друга. По свойству антисимметричности делимости получаем k₁=k₂.

Свойство 6. Если элементы а и b не взаимно просты, то а и b имеют общий делитель, не равный 1.

Доказательство. По условию НОД(a , b)= d¹1. Тогда по определению d и есть не равный единице общий делитель а и b.

Свойство 7. = .

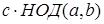Доказательство. Обозначим d =НОД(a , b). По свойству (6) делимости элемент с d делит любой общий делитель элементов ас и b с, следовательно, является их НОД. Свойство доказано.

Свойство 8. Если , то .

Доказательство. Из условия следует, что d делит любой общий делитель элементов а и b и . Тогда по свойству (6) делимости элемент делит любой общий делитель элементов , следовательно, является их НОД. Свойство доказано.

Свойство 9. Если и , то .

Доказательство. Пусть НОД и НОД(а,b) = 1, тогда среди делителей элементов b и с нет делителей элемента а. Следовательно, и среди делителей элемента bc нет делителей элемента а, что и означает, что .

Свойство 10. Если , то для любых N.

Доказательство. Докажем, что методом математической индукции. Пусть m = 1, тогда по условию, т.е. база индукции верна. Предположим, что для всех k < m. Покажем, что при k = m. по свойству (10) для с = b. Отсюда, для всех N. по свойству 3 делимости. Аналогичными рассуждениями получаем для любого N. Следовательно, .

Свойство 11. Если , то для любого .

Доказательство. Пусть , тогда а = sd и c = td для некоторых s,t S таких, что НОД(s,t) = 1. Поскольку , то НОД(s,b) = 1 и по свойству 9 НОД(s,tb) = 1. Следовательно, . Свойство доказано.

Свойство 12. Существование НОК(a , b) влечет существование НОД(a , b) и равенство НОД(a , b) НОК(a , b) = ab .

Доказательство. Если хотя бы одно из чисел или равно 0, то и равенство справедливо. Пусть элементы и ненулевые и 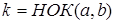. Поскольку - общее кратное чисел и , то для некоторого . Так как и , то - общий делитель и . Докажем, что 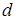делится на любой общий делитель элементов и . Пусть - произвольный общий делитель чисел и , т.е. и для некоторых . Поскольку - общее кратное элементов и , то . Так как , то для некоторого . Отсюда . Следовательно, , и, значит, НОД( ).

Предложение 1. Полугруппа является НОК-полугруппой тогда и только тогда, когда есть НОД-полугруппа.

Доказательство. По свойству 12 достаточно доказать, что любая НОД-полугруппа является НОК-полугруппой. Пусть есть НОД-полугруппа. Возьмем произвольные . Если хотя бы одно из чисел равно 0, то . Рассмотрим случай и . Обозначим . Тогда и для некоторых . Поскольку по свойству 7, то . Положим . Число является общим кратным элементов и . Осталось показать, что на делится любое общее кратное и . Возьмем произвольное общее кратное элементов и , т. е. для некоторых . Тогда , т.е. 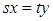(поскольку ). По свойству 11 имеем , значит, для некоторого . Поэтому , т.е. .