Глава 2. Мультипликативные полугруппы неотрицательных чисел

со свойствами (*) и (**)

В этой главе на основе предложения 2 дадим топологическую классификацию полугрупп S, которые обладают одним из следующих свойств:

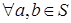(*) (a < b );

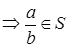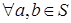(**) (0<a < b ).

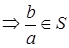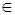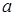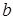Лемма 8. Полугруппа S , удовлетворяющая хотя бы одному из свойств (*), (**) является НОД-полугруппой и НОК-полугруппой. При этом, в первом случае НОД(a,b)= max{a,b}, НОК(a,b)= min{a,b} для любых a , b S , а во втором случае – НОД(a,b)= min{a,b}, НОК(a,b)= max{a,b}, если числа и не равны нулю.

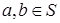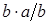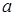Доказательство. Пусть полугруппа S обладает свойством (*). Покажем, что любые два элемента имеют НОД и НОК. По свойству (*) a = и S. Получили, что элемент b является делителем a. Следовательно, по свойству 2 делимости НОД(a,b) = b = max{a,b} и НОК(a,b) = а = min{a,b}. Аналогичными рассуждениями можно показать, что если полугруппа S обладает свойством (**), то для любых ненулевых элементов и 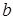НОД(a,b)= min{a,b}, НОК(a,b)= max{a,b}. Пусть хотя бы одно из чисел а или b равно 0, например, b. Тогда НОД(a,b) = НОД(а,0) = а и НОК(a,b) = НОК(а,0) = а.

Лемма 9. Если в полугруппе S со свойством (*) существует элемент c > 1, то S \ {0} – группа.

Доказательство. Докажем, что в S произвольный ненулевой элемент a < 1 обратим. Элемент acⁿ > 1 для некоторого n 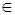N. Тогда 1 / acⁿ 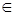S в силу свойства (*). Откуда 1 / a = (1 / acⁿ) cⁿ S.

Предложение 4. Любая полугруппа S со свойством (*) относится к одному из следующих классов:

1. S = [0,1].

2. S = R⁺.

3. S = {rⁿ | n = 0,1,2,…} 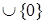, где 0 < .

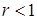4. S = {rⁿ | n 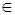Z} 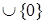, где 0 < .

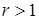5. S – нульмерное плотное подпространство в [0,1].

6. S – нульмерное плотное подпространство в R ⁺ .

7. S = {0,1}.

Доказательство. Если 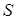связно, S = 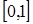или S =R ⁺ по лемме 1.

Пусть S несвязно. Поскольку полугруппа {0}È[1,+ ) не обладает свойством (*), то S нульмерно. Предположим сначала, что S замкнуто (в R ⁺). Если в S ровно два элемента, то S = {0,1}. Пусть поэтому . Покажем, что точка 1 изолирована в S. Предположим, что это не так. Тогда в S существует строго возрастающая последовательность (е _n), сходящаяся к 1. Так как S замкнуто и несвязно, то в (0,1) найдутся такие элементы c < d, что (c,d) = по лемме 4. В то же время строго возрастающая последовательность (e_n,d) элементов из S сходится к числу d. Противоречие. Следовательно, 1 является изолированной точкой в S. Обозначим 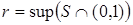. Тогда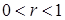 . 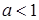Возьмем произвольный ненулевой элемент из 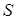. Для него 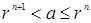при некотором 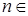N. По свойству (*) получаем 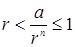и 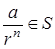. Поскольку 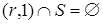, то 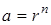. Тогда в случае S имеем 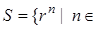0,1,2,… 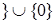, а в противном случае 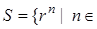Z 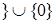по лемме 9.

Пусть S нульмерно и не замкнуто. Существует монотонная последовательность чисел 0 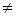а _n 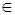S, сходящаяся к некоторому а 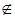S. Пусть b_n = a_n / a_n₊₁, если (a_n) возрастает, и b_n = a_n₊₁ / a_n, если она убывает. Тогда b_n 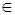S ( 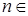N) и b_n 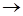1 при 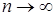. Возьмем произвольное число с 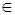(0,1). Для каждого 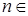N найдется такое k(n) 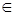N, что 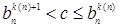. Тогда имеем 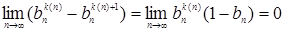и .

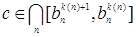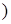Следовательно, числа N из 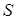образуют плотное подмножество в [0,1]. Если S 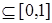, то получаем случай 5. Если же S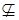 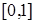, то по лемме 9 получаем случай 6. Предложение доказано.

Предложение 5. Любая полугруппа S со свойством (**) относится к одному из следующих классов:

1. S = R⁺.

2. S = {rⁿ | nÎN} 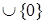, где .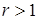

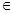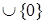3. S = {rⁿ | n Z} , где .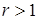

4. S\{0} – нульмерное плотное подпространство в [1, ).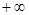

5. S – нульмерное плотное подпространство в R ⁺ .

6. S = {0,1}.

7. 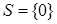È[1,+¥).

Доказательство. Пусть 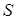связно. Поскольку полугруппа [0,1] не обладает свойством (**), то по лемме 1 получаем S =R ⁺.

Очевидно, 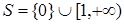является полугруппой со свойством (**).

Пусть далее 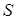несвязно и 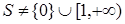. Тогда 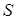нульмерно по предложению 2.

Пусть 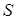замкнуто и 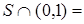Æ. Если в 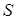нет элемента, большего 1, то 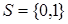. Пусть (1,+¥)¹Æ. Докажем, что точка 1 изолирована в 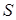. Допустим, что это не так. Тогда в 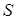существует строго убывающая 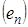последовательность, сходящаяся к 1. Так как 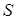замкнуто и несвязно, то в [1,+¥) есть такие элементы 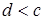, что 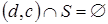. В то же время строго убывающая последовательность 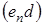элементов из 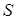сходится к числу 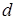, следовательно, ее члены, начиная с некоторого номера, попадают в интервал 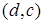. Получили противоречие. Следовательно, 1 является изолированной точкой в 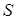. Обозначим . Тогда 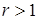и поскольку 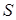замкнуто, то . 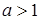Возьмем произвольный элемент из 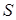. Для него 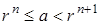при некотором 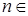N. По свойству (**) получаем 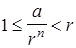и 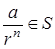. Поскольку 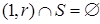, то 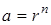. В этом случае 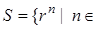N .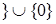

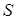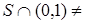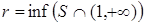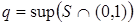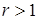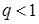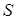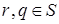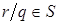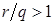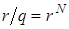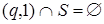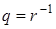Пусть замкнуто и Æ. Как и выше, доказывается, что 1 – изолированная точка. Обозначим и . Тогда , . Так как замкнуто, то . Из свойства (**) следует, что . Из неравенства по доказанному выше получаем: для некоторого натурального N. Поскольку , то . В этом случае 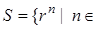Z .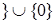

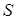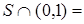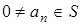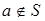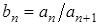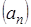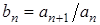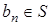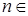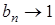Пусть не замкнуто и Æ. Тогда существует монотонная последовательность чисел , сходящаяся к некоторому . Пусть , если последовательность элементов убывает, и , если она возрастает. Тогда для всех N и при 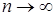. Возьмем произвольное число 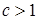. Для каждого 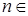N найдется такое 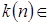N, что 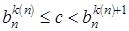. Тогда имеем 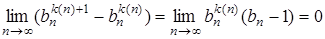и .

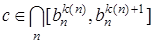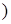Следовательно, числа N из 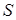образуют плотное подмножество в [1,+ ¥) (случай 4).

Если 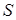не замкнуто и 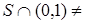Æ, то аналогичные рассуждения показывают, что S – плотное подпространство в R ⁺ .

Следствие 1. Любая полугруппа S , обладающая свойствами (*) и (**) относится к одному из следующих классов:

1. S = R⁺.

2. S – нульмерное плотное подпространство в R ⁺ .

3. S = {0,1}.

Библиографический список

1. Варанкина, В.И., Полукольца непрерывных неотрицательных функций: делимость, идеалы и конгруэнции [Текст] // В. И. Варанкина, Е. М. Вечтомов, И. А. Семенова / Фундаментальная и прикладная математика. 1998. Т. 4. № 2. С 493-510.

2. Курош, А.Г. Лекции по общей алгебре [Текст] / А. Г. Курош. – М.: Наука, 1973.

Дата добавления: 2019-07-15; просмотров: 171; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!