Глава 2. МЕТОДЫ И СРЕДСТВА ПОВЫШЕНИЯ МОТИВАЦИИ УЧЕНИЯ МАТЕМАТИКЕ

Мотивация и природа математических знаний

 

Применить успешно метод мотивации в учебном процессе невозможно без знания природы математических понятий и теорий. Ответить на вопрос «Что такое математика?» так же трудно, как, согласно словам Кузьмы Пруткова, постараться «объять необъятное». Термин «математика» происходит от греческого слова «µбиемб», что означает знания, наука. Это слово происходит от глагола мaхибхщ, что означает учить при помощи суждений и здравого смысла.

Поскольку стадия формальных операций соответствует возрасту 11 лет, а дети начинают учиться с 6 – 7 лет, имеются определённые трудности в формировании внутренней мотивации учения математики. К счастью, школьный курс математики оперирует только конкретными «пространственными формами» и «количественными отношениями». Эти факты позволяют оперировать понятиями числа и фигуры на более ранней стадии развития. Следует отметить, что школьные учебники не содержат какой-либо информации о существовании многих областей математики. Но отдельные способные учащиеся представляют школьную математику как всю математику и стремятся стать специалистами в других областях знаний.

Роль задач с практическим применением в развитии предметной мотивации

 

Ответ на вопрос «Как возбудить интерес к математике?» неоднозначен. Всё зависит от интересов индивидуума. Очевидно, необходимо проанализировать личностные механизмы, активизирующие и регулирующие мотивационную роль практики к учебной дисциплине.

Можно выделить ряд стадий усвоения учебного материала:

1) база понимания формируется на основе наблюдения и эксперимента, выполняет стимулирующую функцию;

2) теоретический уровень достигается в ходе осмысления всей системы эмпирических предпонятий и взаимосвязей между ними;

3) активизация стремления учащихся к применению теоретических сведений на практике формируется, когда понятие и способы деятельности получают некоторые конкретные, содержательные интерпретации.

Реализация данной схемы происходит на протяжении всего процесса обучения математике в школе. Тем не менее, она предусматривает доминирование различных мотивационных факторов в зависимости от возрастного диапазона.

На первой стадии изучение математики представляет собой процесс эмпирического познания, где главная роль принадлежит наблюдению и эксперименту (вычисление, измерение, конструирование и т.д.). Здесь основной мотивационный фактор – это стремление связать усваиваемый материал с собственным практическим опытом. Принцип связи теории с практикой требует гармоничной связи научных знаний с практикой. Важность этого принципа объясняется тем, что практика является отправной точкой процесса познания и критерием истины. В процессе преподавания математики связь с практикой обеспечивается при помощи лабораторных работ или решения упражнений и задач. Практика доказывает необходимость полученных знаний и этим повышает мотивационный уровень учения математики. Любую задачу можно ориентировать на повышение творческих способностей и повышение мотивации учения математики.

Поэтому на следующем этапе, хотя роль практики перестаёт быть доминирующей, тем не менее, она остаётся важным средством мотивировки рассмотрения того или иного фрагмента содержания и возбуждения первоначального интереса к нему. Здесь математический факт является результатом решения чисто математической задачи.

На следующем этапе мотивационная роль практики выражается в реализации её мировоззренческой функции. Н. А. Терёшин указывает, что такая реализация возможна через показ применения изучаемого математического материала смежных курсов и других школьных дисциплин, рассмотрение истории возникновения и эволюции математических понятий и методов, знакомство с элементами математического моделирования реальных состояний и процессов, лежащих в основе овладения прикладной математической идеологией [16, с.3]. При этом осознание роли математических знаний, как важнейшего компонента человеческой культуры, становится одним из ведущих мотивационных факторов, которые обеспечивают осознанное стремление учащихся к применению усвоенного материала в смежных предметах и реальной жизненной практике.

Текстовые задачи являются основным средством демонстрации практической значимости математических знаний. При помощи решения текстовых задач учащиеся знакомятся с основным математическим методом познания действительности – методом моделирования, который предполагает построение математической модели, воспроизводящей особенности исходной реальной ситуации; выбор пути исследования этой модели и его реализацию; анализ и истолкование полученных количественных и качественных результатов.

Каждый человек должен знать, что практически ежедневно мы сталкиваемся, сознательно или не сознательно, с решением математических задач.

 

2.3. Задача Герона Александрийского (I в. До н.э.) (Задача 1)

Из-под земли бьют четыре источника. Первый заполняет бассейн за 1 день, второй - за 2 дня, третий - за 3 дня, четвёртый - за 4 дня. Сколько времени потребуется четырём источникам вместе, чтобы заполнить бассейн?

При решении можно использовать следующий алгоритм:

1. Сколько бассейнов заполняют все источники за 1 день:

2. Сколько времени потребуется, чтобы заполнить 1 бассейн:

На основании этой задачи можно составить различные однотипные задачи, используя следующую общую задачу:

Задача 2

· Из под земли бьют 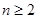 источников. Первый заполняет бассейн за m₁ дней, второй - за m₂ дней,..., п-й - за m_n дней. Сколько времени потребуется всем источникам вместе, чтобы заполнить бассейн?

Частные формулировки общей задачи можно изменить и по содержанию. Для этого вместо «источников» можно взять бригаду, автобусный парк и т.д. К такому типу относится следующая задача.

Задача 3

· Со склада различным потребителям распределяется определённое количество товара. Имеется 5 автопарков. Первый развозит весь товар за 2 дня, второй - за 1 день, третий - за 3 дня, четвёртый - за 4 дня и пятый - за 6 дней. Сколько часов потребуется всем автопаркам, чтобы вместе развести весь товар, если каждый автопарк ежедневно работает 9 часов?

Решение: 1. Сколько товара развозят все автопарки за 1 день:

2. Сколько дней потребуется всем автопаркам, чтобы вместе развезти весь товар:

 (дней).

3. Сколько часов потребуется всем автопаркам, чтобы вместе развезти весь товар:

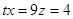 (часа).

Ответ: 4 часа.

Решение задач этого типа убеждает учащихся в единстве математических методов, в единстве связей практики и абстрагирования.

Для учащихся, увлечённых химией, физикой и биологией, важны задачи со следующим содержанием.

Задача 4

· В 100 г 20%-ного раствора соли добавили 300 г её 10%-ного раствора. Определите процентную концентрацию раствора.

Решение:

Графический метод:

Рис. 1

Ответ: 12,5%

Метод последовательных вычислений:

Сколько растворенного вещества содержится:

а) в 100 г 20%-ного раствора? [100•0,2 = 20(г)];

б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)].

Сколько вещества содержится в образовавшемся растворе?

20 г + 30 г = 50 г.

Чему равна масса образовавшегося раствора?

100 г + 300 г = 400 г.

Какова процентная концентрация полученного раствора?

(50/400)100 = 12,5(%).

Ответ: 12,5%

Алгебраический метод:

Пусть х - процентная концентрация полученного раствора. В первом растворе содержится 0,2•100 (г) соли, во втором - 0,1•300 (г), а в полученном растворе - х• (100 + 300) (г) соли. Составим уравнение: 0,2•100 + 0,1•300 = х• (100 + 300). Получаем х = 0,125 (12,5%).

Ответ: 12,5%

Задача 5

· Смешали 10%-ный и 25%-ный растворы соли и получили 3 кг 20%-ного раствора. Какое количество каждого раствора в килограммах было использовано?

Решение:

Алгебраический метод:

а) C помощью уравнения:

Пусть х (кг) - масса 1-го раствора, тогда (кг) - масса 2-го раствора.

Получаем:

- 0,1•х (кг) соли содержится в 1-ом растворе;

- 0,25• (3-х) (кг) соли содержится в 2-ом растворе;

- 0,2•3 (кг) соли содержится в смеси.

Учитывая, что масса соли в 1-ом и 2-ом растворах равна массе соли в смеси, составим уравнение: 0,1х+0,25•(3-х)=0,2•3 или х= 1. Итак:

-х=1 (кг) - масса 1-го раствора;

-3–х = 3–1=2 (кг) - масса 2-го раствора.

Ответ: 1 кг, 2 кг.

б) С помощью системы уравнений:

Пусть х (кг) - количество первого раствора, у (кг) - количество второго раствора. Система уравнений имеет вид:

Ответ: 1 кг, 2 кг.

Графический метод:

 Рис. 2

Ответ: 1кг, 2кг.

Задача 6

· Найти два числа, зная, что их сумма равна 16, а сумма их квадратов - 130.

Для отдельных учащихся, увлечённых другими предметами, полезно решать задачи, связанные по содержанию с любимыми предметами.

Задача 7

· Тело движется по закону , где  и a<0. Определить:

- время начала пути;

- длину пути;

- время остановки тела.

Решение. Эта задача связана с исследованием свойств функций при помощи производной. Обозначим через t 1 время начала пути, а через t 2 – время остановки тела. Производная  равна скорости движения тела.

Для решения этой задачи можно применить метод мозговой атаки.

В этом случае у учащихся последовательно возникают следующие вопросы с соответствующими ответами:

1. При каких условиях тело движется?

Во временном интервале [p, q] тело движется при условиях:

;

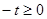-S’(t)>0, как только p < t <q.

2. Каким условиям удовлетворяет момент t ₁ начала пути?

Во первых, . Во вторых, S’( t ₁ ) . 0 и S’(t)<0 при 0 < t < t ₁ .

3. Каким условиям удовлетворяет момент t2 остановки тела?

Во первых, t1 < t 2 . Во вторых, S’(t 2 )= 0 и S’(t)>0 при t1 < t < t 2 .

Выводы: 1. Для решения задачи находим корни х₁, х₂ квадратного уравнения 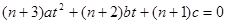. Если корни или мнимые, или равны, или оба неположительные, то задача физического смысла не имеет.

2. Предположим, что корни действительные, х1 < х2 и 0 < х2 . В этом случае t2 = х2 и t1 = max {0, x1}.

Конкретные примеры могут быть построены следующим образом:

- фиксируем действительные числа х1, х2 такие, что х1 < х2 и 0 < х2 ;

- фиксируем положительное число n и отрицательное число p;

- положим a = p:(n+3), b = -p(x1 + x2 ):(n+2), c = p. x1 . x2 :(n+1).

Задача 8

· Калорийность 100г свежей севрюги и 100г осетра составляет 644 ккал. Какова калорийность 100г осетрины, если известно, что она меньше калорийности 100г севрюги на 12 ккал?

Решение. Пусть калорийность 100г осетрины равна x, тогда калорийность 100г севрюги - (x+12). Учитывая, что их общая калорийность составляет 644 ккал, составим и решим уравнение:

x +x+12 = 644,

2x = 632,

x = 316.

Эту задачу можно решить и арифметическим способом.

Приведённые задачи удовлетворяют следующим принципам, которые выделены в пособии Л. М. Фридмана [19]:

1) решение задач используется для формирования у учащихся необходимой мотивации их учебной деятельности, интереса и склонностей;

2) решение задач используется для иллюстрации и конкретизации изучаемого учебного материала;

3) выработка у учащихся определённых умений и навыков;

4) решение задач – удобное и адекватное средство для контроля и оценки учебной работы учащихся;

5) решение задач используется для приобретения учащимися новых знаний.

Выявление практической значимости изучаемых фактов не только возбуждает интерес, но является и сильным стимулом, поскольку взаимосвязан с основными целями обучения.

---

Дата добавления: 2019-07-15; просмотров: 197; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!