Использование макросов для заполнения таблиц
Как уже отмечалось, в ряде случаев, в частности, при расчётах посредством БПФ, требуется заполнять весьма громоздкие таблицы.
Например, требуется заполнить столбец В формулой =ЕСЛИ(A11<0;-1;1) от ячейки В11 до ячейки В4106. Это удобно сделать простым макросом, осуществляющим «протаскивание» этой формулы по заданным ячейкам. Соответствующий макрос создаётся посредством рекордера следующим образом. Выполняются команды Сервис, Макрос, Начать запись…. В открывшемся диалоговом окне вводится название макроса, например, Ст_В_4096 и производятся следующие действия:
– выделение ячейки В11 (в которой уже записана необходимая формула) и «протаскивание» её (за крестик в нижнем левом углу выделенной ячейки) вниз на несколько ячеек, например до ячейки В14;
– останов записи останавливается (квадратной кнопкой) в окошке, появившемся после закрытия окна, в котором вводилось имя макроса;
– открывание диалогового окна Макросы… (команды: Сервис, Макрос, Макросы…)
– выделение названия данного макроса и нажатие кнопки Войти.
 |
В открывшемся окне редактора VBA, показанного на рисунке 28, производится коррекция записанного макроса. Для этого цифры, соответствующие последней ячейке, до которой было произведено «протаскивание» (на рисунке 28 они отмечены овалами), заменяются цифрами ячейки, до которой должен быть заполнен данный столбец (в данном случае цифрой 4106). Макрос готов к работе (заполнению столбца В от ячейки В11 до ячейки В4106). Выполнение макроса – команды: Сервис, Макрос, Макросы…. Выделить название макроса и нажать Выполнить в открывшемся диалоговом окне.
|
|
|
Генерация случайных чисел
В ряде случаев, например, при исследовании случайных последовательностей импульсов, удобно использовать функцию инженерного пакета Excel «Генерация случайных чисел».
Например, необходимо создать случайную последовательность нулей и единиц, с определённой вероятностью их появления. Для этого вначале необходимо заготовить «входной интервал значений и вероятностей». На рисунке 24 такой интервал занимает ячейки В1 и В2 – величины (1 и 0) и ячейки С1 и С2 – вероятности их появления (0,7 и 0,3 соответственно)
Выполним последовательно команды Сервис, Анализ данных…, в открывшемся окне выберем Генерация случайных чисел. Появляется окно (рисунок 29) Генерация случайных чисел. В этом окне устанавливаем распределение Дискретное, входной интервал – указываем ячейки, в которых ранее были установлены величины и вероятности их появления, и ячейки выходного интервала. Нажимаем кнопку ОК и выходной интервал заполняется.
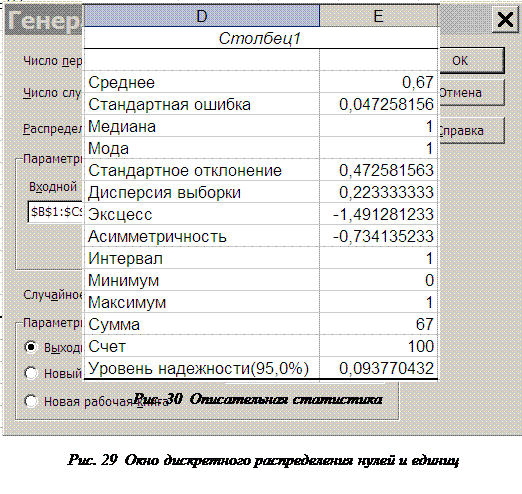
Функция Анализ данных… позволяет убедиться, насколько полученная выборка соответствует заданным условиям. Для этого в окне Анализ данных… следует выбрать опцию Описательная статистика В открывшемся окне следует указать диапазон, в котором находятся анализируемые данные, если необходимо, уровень надёжности в % и верхнюю левую ячейку диапазона выходных данных. На рисунке 30 приведена таблица описательной статистики для ранее полученной последовательности нулей и единиц. Видно, что количество единиц несколько меньше теоретического значения (67 вместо 70), что вполне объясняется малой величиной выборки.
|
|
|
В заключение покажем, как формируется последовательность прямоугольных импульсов, например, биимпульсная последовательность с периодом в 16 интервалов. На рисунке 31 в столбце В (Случ_ед)записана случайная последовательность 1 и -1.Столбец С (Код) заполняется так. Первоначально в первых 16-и ячейках вручную формируется алгоритм биимпульсно 
го кода: первые 8 ячеек повторяют значение первой ячейки столбца В (пусть её номер – В11), то есть в ячейки С11:С18 записывается формула =В11, а в следующие 8 ячеек С – значение ячейки В11 с обратным знаком (=-В11). После чего, как указывалось ранее, записывается макрос для заполнения этого столбца, причём вначале выделяется не одна, а 16 начальных ячеек, которые и «протаскиваются» вниз, например, ещё на 16 ячеек. Коррекция макроса, записанного в данном случае, ничем не отличается от коррекции записанного в случае предыдущем.
|
|
|
Литература
1. Г. Корн, Т. Корн. Справочник по математике. Для научных работников и инженеров. Пер. с англ. под общей редакцией И.Г.Арамановича/ М.:Наука – 1978 – 832 с.:ил
2. В. Я. Гельман. Решение математических задач средствами Excel/ СПб: Питер – 2003 – 240 с.:ил.
3. http://office.microsoft.com
| Оглавление | |
| 1. Общие рекомендации по использованию приложения Microsoft Office Excel | 3 |
| 1.1. Microsoft Office Excel 2003 ………………………………………….. | 3 |
| 1.2. Microsoft Office Excel 2007 ………………………………………….. | 15 |
| 2. Быстрое преобразование Фурье в приложении Microsoft Excel | 17 |
| Краткая теория ……………………………………………………………………...... | 17 |
| БПФ в приложении Excel ……………………………………………………... | 18 |
| Практика использования БПФ в приложении Excel ……………………… | 21 |
| 3. Использование макросов для заполнения таблиц | 24 |
| 4. Генерация случайных чисел | 26 |
| Литература …………………………………………………………………… | 29 |
|
|
|
[1]Примеры рассматриваются здесь применительно к наиболее распространённой версии Office 2003; но все общие соображения применимы в полной мере и к версии Office 2007.
Дата добавления: 2019-03-09; просмотров: 1060; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!