Практика использования БПФ в приложении Excel
Следует обратить внимание на два обстоятельства использования БПФ в приложении Excel. Во-первых, очень часто исследуемая функция задаётся некорректно. Во-вторых, во многих случаях требуется значительное число элементов дискретизации функции, например, при исследовании случайных сигналов (до 4096 – предельного числа элементов дискретизации в приложении Excel), что вызывает трудности ввода, как исходных данных, так и формул для их обработки.
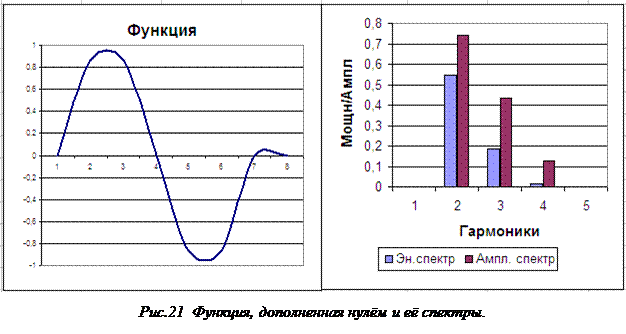
Рассмотрим первое. В большинстве руководств по использованию БПФ (в различных приложениях) указывается, что, если число дискретных значений исследуемой функции отличается от двух в целочисленной степени, то данное число дискретных значений нужно дополнить до названного числа нулями. Это нежелательно. Обратимся к простейшему примеру. На рисунке 21 приведена исходная синусоидальная функция, число дискретных значений которой равно 7, а потому это число дополнено одним нулём. Очевидно, периодическая функция, определённая по заданной (см. рисунок 15), будет иметь разрыв и, следовательно, в её спектре появятся высшие гармоники, которых не должна иметь синусоидальная функция
Далее. Часто пределы дискретизации выбираются так, чтобы период функции полностью помещался в заданном интервале Т. Это также приводит к разрыву периодической функции и появлению высших гармоник, наличие которых обычно объясняют или малым числом рассматриваемых периодов (на интервале Т), или недостаточным количеством членов разложения (что принципиально неверно). Рисунок 22 иллюстрирует этот случай, а на рисунке 23 показана корректно заданная синусоидальная функция и её спектры. Видно, что, несмотря на малое число членов разложения и единственный период исходной функции, спектры отвечают теоретической предпосылке (синусоидальная функция имеет единственную спектральную составляющую – первую гармонику).
|
|
|
Таким образом, дискретизировать исследуемую функцию нужно так, чтобы следующее за ней мгновенное значение (в начале следующего периода Т) равнялось первому мгновенному значению функции в данном периоде Т.
Второе. Если использование БПФ носит исследовательский характер, необходимо использовать большое число членов разложения, вплоть до предельного (в Excel это число равно 4096). Очевидно, что в таком случае возникает сложность заполнения таблиц с большим количеством строк данными и формулами. Однако это затруднение легко преодолевается с помощью простейших макросов, построенных по линейным алгоритмам. При создании таких макросов от пользователя не требуется ни знания языка программирования VBA, на котором эти макросы записываются, ни заметных затрат времени. Это возможно посредством встроенной в приложение Excel функции рекордера, последовательно записывающей в макрос все действия пользователя. Покажем это на примере исследования спектра случайной биимпульсной последовательности (рисунок 24)
|
|
|
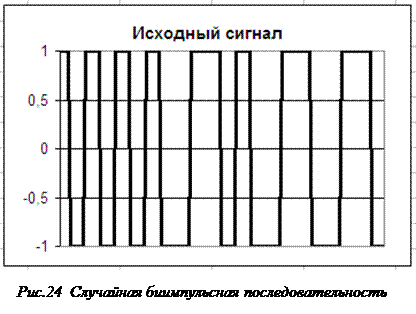В исходной биимпульсной последовательности единицы передаются комбинацией импульсов 1; -1, а нули - -1; 1, причём длительность каждого импульса равна половине тактового интервала Т/2. Произведём БПФ для предельного числа дискретных элементов – 4096-и, что соответствует 2048 периодам частоты высшей гармоники данной последовательности (частоты Найквиста – Котельникова).
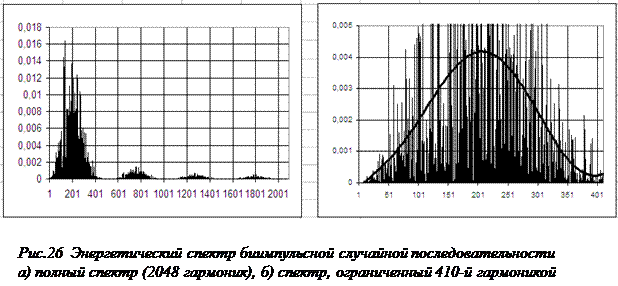
Примем период последовательности равным 16-и дискретным значениям (по 8-и значений для положительного и отрицательного импульсов). На рисунке 25 показан начальный участок данной последовательности. Если считать частоту разложения равной 2048 условным единицам (по предельному числу периодов), то тактовая частота импульсной последовательности будет равна 4096/16 = 256. На рисунке 26 приведены графики полного энергетического спектра исходной последовательности а) и его начального участка б). На последнем присутствует линия тренда, аппроксимированная полиномом 6-й степени. На рисунке хорошо видно, что спектральный максимум находится на частоте, ниже тактовой, что характерно для случайной биимпульсной последовательности.
|
|
|
Линия тренда может быть получена следующим образом. Правой кнопкой мыши следует щёлкнуть по ряду данных на соответствующем графике. В выпадающем меню следует левой кнопкой выделить Добавить линию тренда…. При этом открывается окно, показанное на рисунке 27. Далее следует выбрать тип аппроксимации, задать, если это требуется, соответствующие параметры и нажать ОК. Линия графика формируется так же, как и другие линии.
 |
Помимо наглядного представления спектров заданной случайной последовательности, полученные результаты позволяют оценить относительную мощность того или иного участка спектра, найти экстремумы спектрального распределения и многое другое. Ограниченность статистического материала (исследуется всего 256 периодов последовательности) может быть легко восполнена многократным повторением опыта.
Дата добавления: 2019-03-09; просмотров: 1120; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!