Быстрое преобразование Фурье в приложении Microsoft Excel

Федеральное агенство связи РФ

Московский технический университет связи и информатики

Кафедра многоканальной электросвязи

Тверецкий М.С.

Рекомендовано УМО по образованию в области телекоммуникаций в качестве учебного пособия для студентов, обучающихся по направлению подготовки дипломированных специалистов 210400 – «Телекоммуникации» и направлению подготовки бакалавров 210700 – «Инфокоммуникационные технологии и системы связи»

многоканальные

телекоммуникационные системы

(компьютерные упражнения)

Часть 1

Методические указания по выполнению упражнений

Москва 2011

УДК. 621.395.4

004.021

Тверецкий М.С. Многоканальные телекоммуникационные системы (компьютерные упражнения). Ч. 1. Методические указания по выполнению упражнений. Учебное пособие / МТУСИ. – М., 2011. – 30 с.: ил.

Пособие предваряет серию сборников компьютерных упражнений по курсу «Многоканальные телекоммуникационные системы», разработанных на базе математического процессора Office Excel. В части первой серии пособий даются методические указания по выполнению упражнений, разработанных на базе математического процессора приложения Microsoft Office Excel. Особое внимание в пособии уделено инженерному пакету названного приложения.

Ил. 31, табл. 1, список лит. 3 назв.

Рецензенты

связи и информатики, 2011

Компьютерные упражнения по курсу «Многоканальные телекоммуникационные системы» разработаны на базе математического процессора Office Excel. Выбор приложения Microsoft Office Excel был сделан на основе следующих соображений. Во-первых, данное приложение весьма распространено и большинство пользователей ПК имеет навыки работы с ним. Широкое распространение этого приложения позволит выполнять упражнения, как в домашних условиях, так и практически в любых компьютерных классах. Во-вторых, в программы упражнений могут оперативно вноситься поправки преподавателем, ведущим занятия, без обращения к услугам профессионального программиста. В-третьих, расчёты посредством Office Excel корректны и наглядны и не требуют специальных уточнений относительно скрытой от пользователя цифровизации данных, как, например, в приложениях LabView или Mathcad. Конечно, выбранное приложение не свободно от недостатков, однако большинство из них, так или иначе, преодолеваются по мере накопления навыка работы с приложением, как студентами, так и преподавателями.

Общие рекомендации по использованию приложения Microsoft Office Excel

Работа с компьютерными учебными материалами, созданными с использованием приложения Microsoft Office Excel, имеет некоторые особенности. Прежде всего, следует указать, что в любом приложении Excel возможно защитить, как минимум, только целый лист книги. Однако при наличии защиты в лист нельзя вводить какие-либо данные. Поскольку в процессе выполнения упражнений в листы Excel необходимо вводить данные, все листы не защищёны. Поэтому, во избежание невозможности продолжать работу после случайного искажения информации (формул, констант ит.д.) в служебных ячейках, перед началом работы обязательно следует создать резервную копию соответствующего материала, желательно на внешнем носителе.

Работа с учебными материалами возможна, как с использованием Excel 2003, так и Excel 2007. Поскольку приложение Excel 2003 наиболее распространено, обратимся вначале к его особенностям.

Microsoft Office Excel 2003

При установке пакета Microsoft Office 2003 некоторые, необходимые функции Excel не инициализируются. К ним относятся функции Подбор параметра…, Поиск решения… и Анализ данных…. Инициализация функции Подбор параметра… проста: для этого в открытой книге следует выделить в главном меню раздел Сервис и в открывшемся подменю – название данной функции. Если эта функция не инициализирована, то откроется диалоговое окно, в котором будет предложено установить данный компонент. Функции Поиск решения… и Анализ данных… относятся к надстройкам Excel. Для их инициализации в подменю раздела Сервис следует выделить Надстройки… . Откроется диалоговое окно, показанное на рисунке 1. Следует установить флажки перед соответствующими названиями (обязательно перед Analysis ToolPak VBA, Пакет анализа и Поиск решения) и нажать кнопку ОК. Возможно, что программа-установщик не найдёт необходимых файлов и запросит дистрибутив Microsoft Office Excel 2003 (диск, с которого устанавливалось это приложение).

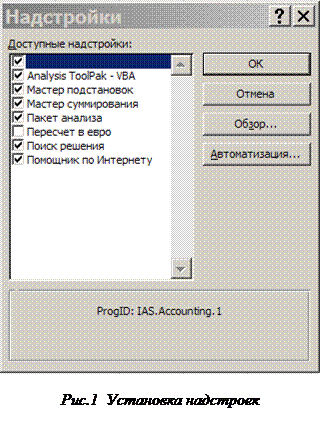После инициализации указанных функций следует установить параметры вычислений. Для этого в подменю Сервис выделить пункт Параметры… и в открывшемся окне (рисунок 2) перейти на вкладку Вычисления. Установить флажки и значения так, как показано на этом рисунке.

Функция Подбор параметра… часто применяется для вычисления значения аргумента по заданной величине функции без её аналитического преобразования в обратную функцию. Например, известно соотношение между дополнительными потерями в оптическом тракте А_дп и «эпсилон-фактором» ε, отображающим уширение импульса из-за хроматической дисперсии среды распространения оптического сигнала

Запишем эту формулу в ячейку А2 листа Excel, как это показано на рисунке 3. Заметим, что формула в синтаксисе Excel отобразилась в строке формул, видной в верхней части рисунка. Установив в ячейке В2 значение ε равным 0,3 получаем величину А_дп = 0,97325 дБ. Произведём теперь поиск значения ε, при кото
ром А_дп равнялось бы двум децибелам. Для этого вызовем функцию Подбор па 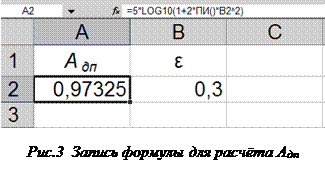раметра … (Сервис →Подбор параметра …) и в открывшемся диалоговом окне установим значения, как показано слева на рисунке 4. Нажимая кнопку ОК, получаем результат, который отображается в окне Результат подбора параметра, показанном на рисунке 4 справа. Если результат удовлетворителен, нажимаем ОК, окно закрывается, а полученные значения сохраняются в ячейках листа. При нажатии кнопки Отмена окно закрывается, а в ячейках восстанавливаются первоначальные значения. Заметим, что в окне Подбор параметра достаточно вручную осуществить только набор значения. Запись координат ячеек осуществляется последовательным выделением в окошке окна Подбор параметра и соответствующей ячейки на листе Excel. Заметим также, что при подборе параметра для уравнения, имеющего несколько решений, следует устанавливать начальное значение аргумента, близкое к его искомому значению. Например, подбирая значение для cosx, равное 0,9, и установив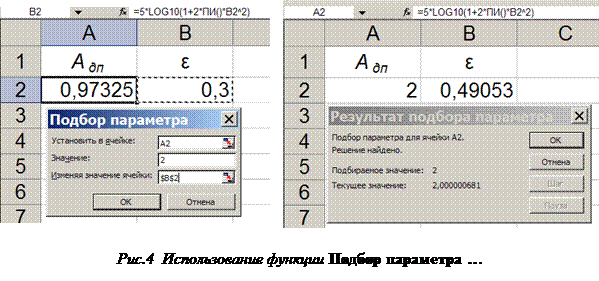
исходное значение х = 0, мы получим 0,45103, а установив х = 2π, получим 6,73423.

В большинстве случаев расчёты в Excel иллюстрируются диаграммами. Наиболее часто используются диаграммы-графики и диаграммы-гистограммы, а иногда также и смешанные диаграммы, например, график и гистограмма на одной оси. При построении диаграмм удобно использовать встроенный Мастер построения диаграмм, однако в ряде случаев диаграмма, построенная с помощью Мастера…, требует некоторой корректировки. В качестве примера рассмотрим построение диаграммы двух гармонических функций, значения которых представлены в таблице, верхняя часть которой показана на рисунке 5.

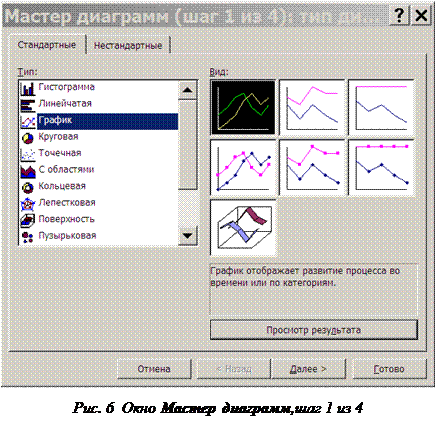
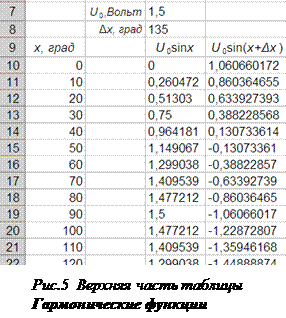Для построения диаграммы вызывается Мастер построения диаграмм… или последовательным выделением пункта главного меню Вставка и пункта Диаграмма… в выпадающем подменю, или посредством клика на значке Диаграмма… на стандартной панели инструментов. При этом открывается окно Мастер диаграмм (шаг 1 из 4):… показанное на рисунке 6. Заметим, что комбинированные диаграммы находятся на вкладке Нестандартные.

Выбираем пункт График и вид графика, как показано на рисунке 6, и нажимается кнопка Далее >. Появляется окно Мастер диаграмм (шаг 2 из 4):…. В этом окне следует открыть вкладку Ряд и нажать кнопку Добавить. Далее следует ввести имена рядов, их значения и значения, которые должны быть отражены на оси абсцисс. К сожалению, раздельное форматирование в именах рядов невозможно, например одновременное использование строчных и подстрочных символов. Поэтому, имя такого вида, как U₀sin(x+Δx), следует или как-то обозначить, или заменить, например, на Usin(x+dx). В дальнейшем, на готовой диаграмме можно будет произвести некоторые изменения.

После ввода имени ряда следует перевести курсор в окно Значения, после чего в таблице мышью выделить ячейки значений данного ряда. В окне автоматически запишется, например =Лист1!$C$10:$C$55, где Лист1! – название листа, а $C$10:$C$55 – диапазон ячеек с данными ряда.

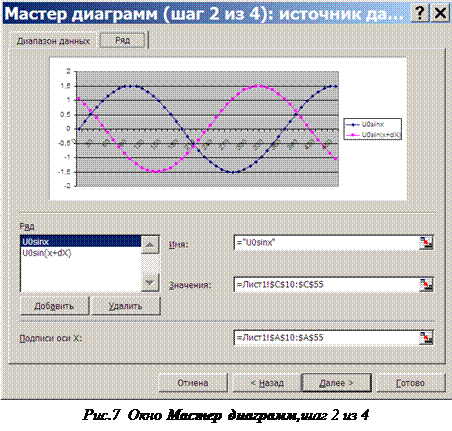
После нажатия кнопки Добавить, аналогично ввести имя и данные для другого ряда и так далее. После ввода параметров рядов курсор переводится в окно Подписи по оси Х и в таблице выделяются ячейки, содержащие значения х. Окно Мастера после указанных действий, представлено на рисунке 7.

Нажимая кнопку Далее>, переходим к окну Мастер диаграмм (шаг 3 из 4):…. На вкладке Заголовки вводим названия диаграммы, осей, например, «Гармонические функции», «х, град», «u, Вольт», и переходим на вкладку Оси. На этой вкладке устанавливаем флажки: ось Х (категорий) и ось Y (значений). Переключатель оси Х устанавливаем в положение автоматическая. На вкладке Линии сетки отмечаем флажками основные линии для обеих осей. На вкладке Легенда устанавливаем флажок Добавить легенду и указываем её размещение, например, справа. Другие вкладки в данном случае не используются.

Переходим с следующему окну Мастера и указываем где следует разместить диаграмму. После нажатия кнопки Готово на листе появляется диаграмма (рисунок 8), которую в большинстве случаев следует откорректировать, особенно если предполагается её чёрно-белая распечатка. Коррекция обычно заключается в следующем.

Изменение фона области диаграммы. Для этого следует кликнуть правой кнопкой мыши на области диаграммы и в выпадающем меню выбрать пункт Формат области построения…. В открывшемся окне установить переключатель в положение Заливка обычная и нажать кнопку ОК. В результате фон диаграммы становится белым.

Изменить вид графиков. Кликнуть правой кнопкой мыши на линии соответствующего графика и выбрать из выпадающего меню пункт Формат рядов данных…. На вкладке Вид открывшегося окна установить вид графика (изменить или убрать маркёры, изменить вид линии). В нашем случае маркёры расположены слишком часто, однако, в дальнейшем, при форматировании оси Х (категорий) их количество может быть существенно уменьшено. Чтобы различать графики при чёрно-белой печати при отсутствии маркёров устанавливают различные типы линий, но, к сожалению, в приложении Excel линии, кроме непрерывной, отображаются неудовлетворительно. В нашем случае – на одном графике оставлены уменьшенные маркёры, а линия второго графика выбрана узорной и максимальной ширины.

Изменить вид осей координат. Кликнуть правой кнопкой мыши на оси абсцисс. В выпадающем меню выбрать пункт Формат оси…. В появившемся окне выбрать вкладку Вид и установить переключатель Метки делений в положение внизу. При этом подписи на оси абсцисс устанавливаются под графиками. На вкладке Шкала установить:

Пересечение с осью Y (значений) в категории номер: – 1;

Число категорий между подписями делений: – 9;

Число категорий между делениями: – 3.

Флажок из окна Пересечение с осью Y (значений) между категориями убрать. При этом начала графиков будут совпадать с нулём на оси Х, а не сдвинуты вправо, как на рисунке 8. Девять категорий между делениями (см. рисунок 5) будет соответствовать подписям на оси Х (категорий), кратным 90 градусам, а число категорий между делениями, равное трём, будет соответствовать цене деления 30 градусов.

Откорректировать легенду диаграммы. Кликнуть правой кнопкой мыши на области легенды и выбрать пункт Формат легенды… из выпадающего меню. На вкладке Вид установить переключатель на пункте Рамка невидимая. На вкладке Размещение установить переключатель на пункте вверху, посередине.

Если на компьютере установлено приложение, позволяющее копировать области в окне как рисунки, например, ABBYY Screenshot Reader, можно скопировать отформатированные названия рядов из ячеек и закрыть ими соответствующие надписи легенды. После чего следует сгруппировать объект Диаграмма и установленные надписи. Окончательный вид диаграммы показан на рисунке 9. Следует заметить, что после операции группировки работа с Мастером диаграмм невозможнжа.

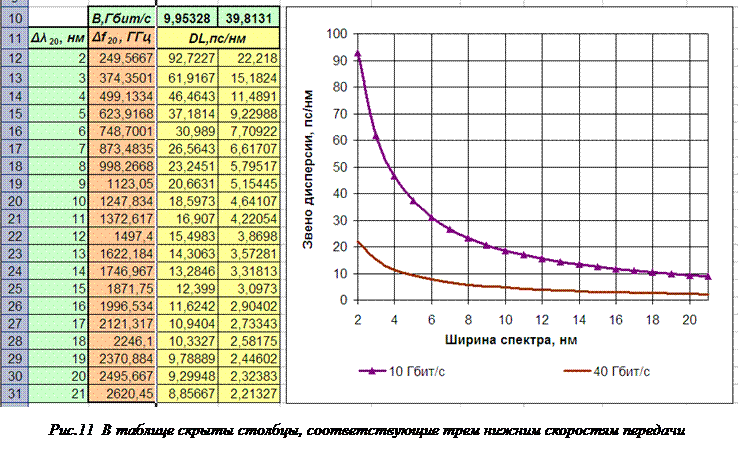
Следующая рекомендация относится к способу оперативного управления графиками. На рисунке 10 приведена таблица величин звеньев дисперсии DL, пс/нм в зависимости от ширины спектра источника излучения Δλ₂₀, нм и скорости передачи В, Гбит/с. Очевидно, что на графиках для скоростей выше 0,622 Гбит/с отсчёты производить невозможно. Поэтому при анализе графиков высоких скоростей следует скрыть столбцы, соответствующие низким скоростям, как это показано на рисунке 11. Для этого надо выделить указанные столбцы, вызвать для них правой кнопкой мыши подменю и выполнить (левой кнопкой) команду Скрыть. (Возврат к прежнему виду достигается выделением столбцов, соседних со скрытыми, вызовом правой кнопкой мыши подменю и выполнением команды Отобразить.) Из рисунка видно, что скрытие указанных столбцов позволяет существенно увеличить масштаб высокоскоростных графиков по вертикали и, следовательно, производить на них отсчёты.

Аналогичные операции можно осуществлять и со строками таблицы. На рисунке 12 показано, что скрытие строк, соответствующих малым величинам ширины спектра излучателя позволяет детализировать «хвосты» графиков. Операции по скрытию строк аналогичны операциям по скрытию столбцов, но при этом выделяются не столбцы, а строки. Возможно одновременное скрытие, как столбцов, так и строк.

Работа с диаграммой удобна в «Окне диаграммы», которое открывается из подменю, вызываемым правой кнопкой мыши при курсоре, установленном на области диаграммы. С помощью мыши окно может быть раздвинуто до размеров, удобных для работы, например, для изменения областей категорий, после чего закрыто без потери данных. Работа с окном диаграммы иллюстрируется рисунком 13.

Microsoft Office Excel 2007

Работа с приложением Microsoft Office Excel 2007 отличается от работы в Excel 2003 только операциями начальной настройки и другим расположением элементов управления (Лента – вместо панелей управления и наличием Панели быстрого доступа).

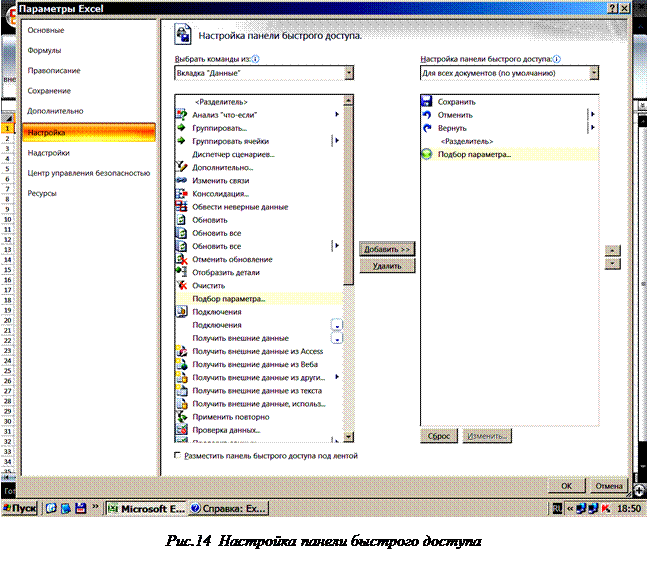
Для настройки функции Подбор параметра… следует нажать на главную кнопку Office и на панели выпадающего меню нажать кнопку Параметры Е xcel (находится внизу справа). Появится палитра Параметры Е xcel (рисунок 14), на которой выделить команду Настройка – и в появившемся окне Настройка панели быстрого доступа последовательно установить: Выбрать параметры из:, Вкладка «Данные», затем найти и выделить функцию Подбор параметра…, которую перенести на левую панель кнопкой Добавить>>.

Далее аналогичным образом из вкладки Все команды на панель быстрого доступа перенести функцию Надстройки…. Закрыть окно параметров и нажать кнопку Надстройки… на панели быстрого доступа. Появится окно надстроек, как на рисунке 1. В этом окне обязательно установить флажки против функций Поиск решения и Пакет анализа (можно установить флажки против всех функций), после чего окно надстроек закрыть (кнопку Надстройки… теперь можно удалить с панели быстрого доступа, для чего нажать на неё правой кнопкой мыши и в выпадающем меню выбрать команду Удалить с панели быстрого доступа).

Функции Поиск решения и Пакет анализа (теперь эта функция будет называться Анализ данных) находятся на ленте (вкладка Данные, подменю Анализ). Функции Мастер подстановок и Мастер суммирования также находятся на ленте , но на вкладке Формулы, подменю Решения. Они также поменяли названия: Мастер подстановок – на Решения, а Мастер суммирования – на Частичная сумма.

Добавим, что пакет Microsoft Office обладает мощной справочной базой, которой и следует пользоваться при возникновении затруднений.

Быстрое преобразование Фурье в приложении Microsoft Excel

Гармонический анализ сигналов электросвязи, в основе которого лежат преобразования Фурье, является одним из фундаментов, на котором построены научные исследования и инженерные расчёты телекоммуникационных систем. Однако, общем виде преобразования Фурье требуют довольно трудоёмких операций, которые значительно облегчаются при переходе к дискретным функциям. Дальнейшее сокращение вычислений достигается при применении алгоритмов быстрого преобразования Фурье (БПФ), позволяющих относительно просто осуществлять построение спектров функций, заданных дискретными мгновенными значениями во временной области. Эти алгоритмы входят во многие компьютерные программы, а также реализованы самостоятельно на различных языках программирования. Особый интерес представляет БПФ, входящее в пакет анализ данных… приложения Microsoft Excel, поскольку это приложение имеется практически на всех персональных компьютерах и практически все пользователи имеют опыт работы с ним. К этому следует добавить, что расчёты посредством вышеуказанного приложения достаточно корректны и хорошо отображаются графически. Построение спектра функции по заданным мгновенным значениям осуществляется прямым БПФ; обратное преобразование позволяет по заданному спектру получить соответствующую временную функцию.

Краткая теория

Напомним кратко основные положения преобразования Фурье в той мере, в какой они потребуются для пояснения использования БФП в приложении Microsoft Excel. Более детальное изложение данного вопроса читатель легко найдёт в многочисленных математических пособиях разного уровня, например, в [1, 2].

Суть дискретного преобразования Фурье заключается в том, что функция, заданная на интервале от 0 до T равномерно расположенными N мгновенными значениями, может быть представлена гармоническим рядом вида

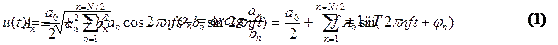где а₀/2 – среднее значение функции (постоянная составляющая); а также

Коэффициенты a_n и b_n находятся по формулам дискретного преобразования Фурье, причём анализируемая функция представляется периодической, как это показано на рисунке 15.

Дискретное преобразование Фурье требует довольно громоздких вычислений; для преодоления этого недостатка были разработаны алгоритмы быстрого преобразования Фурье (БПФ). Действительно, если дискретное преобразование Фурье требует примерно n² арифметических операций с комплексными числами, то БПФ обходится количеством операций равным nlog₂n, но при этом, что очень важно, число n должно быть равно двум в целочисленной степени.

БПФ в приложении Excel

БПФ входит в пакет анализа данных, который находится в пункте главного меню Сервис[1] (по умолчанию этот пакет при установке приложения не устанавливается, его следует установить, выбрав в подменю Сервис пункт Надстройки, и в открывшемся окне установить флажок против пункта Пакет анализа).

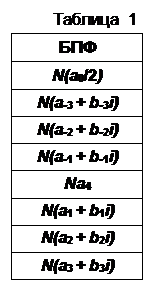Если пакет анализа данных установлен, то после выполнения команд Сервис, Анализ данных…, Анализ Фурье, выводится диалоговое окно (рисунок 16), в котором надо установить входной и выходной диапазоны (установив переключатель в положение Выходной интервал) и нажать кнопку ОК.

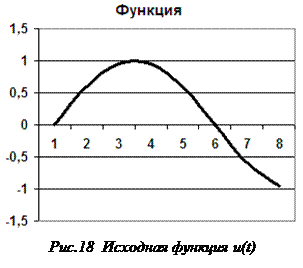
Результат вычисления находится в столбце БПФ (рисунок 17). Интерпретация результата представлена в таблице 1, обозначения в которой соответствуют обозначениям в формуле (1). Поскольку преобразование Фурье является комплексным, результаты вычислений являются комплексными числами. Кроме того, спектр функции формально дополняется отрицательными частотами (коэффициенты с отрицательными индексами в таблице). В верхней ячейке отображается постоянная составляющая (а₀/2), а в пятой – коэффициент (а₄) при частоте Найквиста (Котельникова) – высшей гармонике ряда, равной половине частоты дискретизации данной функции (в этом примере частота дискретизации равна N = 8). В нашем случае за исходную функцию принят отрезок синусоиды, представленный на рисунке 18. Из сравнения рисунков 15 и 18 очевидно, что спектр этой функции должен содержать как постоянную составляющую, так и ряд высших гармоник. Это подтверждается результатами БПФ, представленными на рисунке 17 (все ячейки столбца БПФ заполнены).

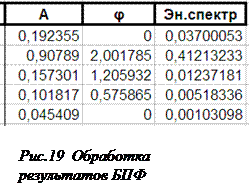
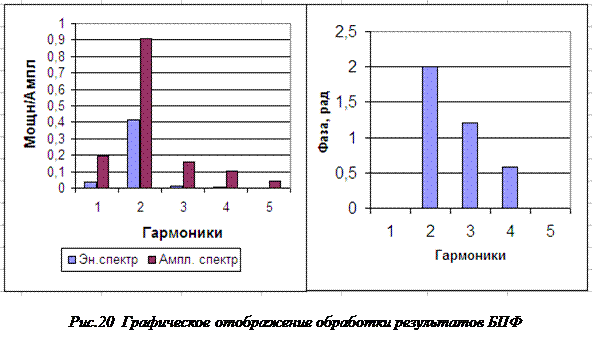
Для дальнейшей работы результаты следует привести к виду формулы (1), то есть определить коэффициенты А _n и фазовые углы φ _n. При этом следует учитывать, что при отказе от отрицательной части спектра (несущей избыточную информацию), все коэффициенты A_n следует удвоить [7], за исключением коэффициентов при постоянной составляющей A₀ и частоте Найквиста – Котельникова A_N_/2. То есть A_n = 2|Ф _n|/N, кроме А₀ = |Ф₀|/N и A_N = |Ф_N|/N, где Ф – величины, полученные в результате БПФ. Составляющие энергетического спектра определяются как A_n и A_N, возведённые в квадрат и поделённые на 2 (приведённые к мощности синусоидального сигнала). Коэффициент А₀ на 2 не делится, поскольку он определяет постоянную составляющую. На рисунке 19 представлены результаты названных расчётов (продолжение таблицы рисунка 17), а на рисунке 20 – графики, соответствующие этим результатам.

Заметим, что модуль комплексного числа в приложении Excel вычисляется по встроенной формуле =МНИМ ABS(), а фаза – по = ─ МНИМ.АРГУМЕНТ(). Знак минус в последней формуле не случаен, поскольку практически удобнее работать с верхними строчками таблицы, в которых располагаются коэффициенты отрицательных составляющих спектра.

Дата добавления: 2019-03-09; просмотров: 6440; Мы поможем в написании вашей работы!
Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!