Методы неиспользующие производные

Цель работы – изучение вопросов решения задач нелинейного программирования с помощью градиентных методом.

Содержание работы

Методы оптимизации, не использующие производные обычно называются методами поиска. В типичном методе поиска направление оптимизации полностью определяется на основании последовательных вычислений целевой функции f(x).

К числу общих особенностей всех методов поиска следует отнести относительную простоту соответствующих вычислительных процедур, которые легко реализуются и быстро корректируются. Здесь отпадает необходимость в вычислении производных, которые требуют довольно большое время на подготовку задачи к решению, а в задачах с достаточно большим количеством переменных довольно трудно получить их аналитические функции, применение же разностных схем приводит к ошибкам, которые, особенно в окрестности экстремума, могут ограничить применение подобной аппроксимации. Методы поиска не требуют регулярности и непрерывности целевой функции и существования производных. Эти методы, хотя и могут требовать более значительных затрат времени, особенно в случаях простых задач, на практике могут оказаться более удовлетворительными с точки зрения пользователя, и решение задачи с их помощью может обойтись дешевле, если стоимость подготовки задачи к решению высока по сравнению со стоимостью машинного времени.

Релаксационный метод (метод Гаусса-Зейделя)

В качестве направления поиска в данном методе предлагается выбрать направление координатных осей. Если выбрана некоторая начальная точка X⁰⁰, где первый индекс показывает цикл, а второй - шаг поиска в цикле, то процесс поиска состоит в следующем.

Первый шаг делаем вдоль координатной оси X₁, тогда новая точка имеет координаты

Величина шага выбирается такой, чтобы в новой точке X⁰¹ можно было найти экстремум функции f(X) вдоль выбранного направления. С этой целью может быть использован как постоянный шаг, так и шаг, определяемый с помощью методов одномерного поиска.

Следующий шаг делается вдоль координатной оси X². Координаты новой точки

Аналогично осуществляется n шагов, где n - число переменных в исследуемой функции. На этом заканчивается первый цикл, после чего описанная процедура повторяется начиная с координатного направления X₁. В общем случае координаты новой точки определяются по формуле

Процесс поиска экстремума может быть прекращен, если значения функций после двух последовательных циклов мало отличаются

½f(X^k^,ⁿ)-f(X^k^-1,ⁿ)½ £ e.

Если исследуемая функция является сепарабельной, т. е.

что говорит об отсутствии взаимного влияния переменных, то экстремум функции может быть достигнут не более чем за n шагов.

Рассмотрим процесс поиска максимума функции f(X)=1–2X₁²–X₂² согласно описанному алгоритму. В качестве начальной точки выберем X=[–3;–3]^Т. Тогда

Подставим эту точку в исследуемую функцию:

f(X)=1–2(–3+t)2–(–3)=j(t).

Величина шага t может быть найдена, например, с помощью метода золотого сечения. Поскольку выражение для функции j(t) довольно просто, применим аналитический путь определения экстремума:

отсюда t=3. Следовательно, координаты новой точки X⁰¹=[0;–3]^Т.

Аналогично на координатной оси X₂

В данном случае

f(X) = 1- 02 - (-3+t)2 = j(t).

Отсюда

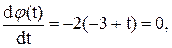
т.е. t=3. Таким образом, координаты новой точки X⁰²=[0;0]^Т.

Проделав новый цикл поиска, легко убеждаемся, что последующие шаги равны нулю. Если в выражении для целевой функции имеется взаимодействие переменных, такой алгоритм работает плохо.

Прямой поиск

Предложенная Хуком и Дживсом логически простая стратегия поиска является одним из первых алгоритмов, в которых при определении нового направления поиска учитывается информация, полученная на предыдущих итерациях. По существу процедура Хука-Дживса представляет собой комбинацию исследующего поиска с циклическим изменением переменных вокруг базисной точки и ускоряющего поиска по образцу с использованием определенных эвристических правил.

Данный алгоритм прямого поиска состоит из следующих операций.

Задается начальная точка X⁰ и начальное приращение DX. Величина шага может быть различной для разных координатных направлений. Чтобы начать исследующий поиск, следует вычислить значение функции f(X) в базисной точке, в качестве которой в первом цикле выбрана начальная точка. Затем каждая переменная (каждый раз только одна) изменяется в циклическом порядке на выбранные величины до тех пор, пока все параметры не будут изменены.

Эти изменения осуществляются следующим образом. Сначала дается приращение переменной X₁, в результате получаем точку

X₁¹=X₁⁰+DX₁⁰.

Если приращение приводит к улучшению функции f(X), переходим в данную точку, в противном случае X₁⁰ изменяем на DX₁⁰ и вычисляем значение функции в точке X₁⁰–DX₁⁰.

При улучшении значения функции в точке X₁⁰–DX₁⁰ выбирается эта точка, в противном случае X₁⁰ остается без изменений.

Затем изменяем X₂⁰ на величину DX₂⁰. И так до тех пор, пока не будут изменены все не зависимые переменные, что завершает исследующий поиск. На каждом шаге или сдвиге по независимой переменной значение целевой функции сравнивается с ее значением в предыдущей точке. При улучшении значения функции на данном шаге старое ее значение в последующих значениях заменяется на новое. Однако если произведенное возмущение по Х неудачно, сохраняется прежнее значение f(X).

После проведения одного (или более) исследующего поиска применяется стратегия поиска по образцу. Удачные изменения в исследующем поиске определяют в Eⁿ вектор, указывающий некоторое направление поиска экстремума, которое может привести к успеху. Новая точка образца рассчитывается по формуле

X² = 2X¹ – X^B,

где X^B=X⁰– координаты старой базисной точки.

Вдоль этого направления может быть проделана серия ускоряющих шагов, пока улучшается функция f(X). Длина шага при поиске по образцу в данном координатном направлении приблизительно пропорциональна числу удачных шагов, проделанных во время исследующих поисков за несколько предыдущих циклов.

Для определения успеха или неудачи по образцу проводят исследующий поиск, который будет называться исследующим поиском типа II. Процедура поиска полностью совпадает с описанной выше. В результате приходим в новую точку X³. Если функция f(X) не улучшилась в процессе исследующего поиска типа II по сравнению со значением функции в базисной точке (в нашем случае X^B=X¹), возвращаемся в базисную точку. В данном случае поиск по образцу считается неудачным, и проводим новый исследующий поиск типа I. Если и он неудачен, последовательно уменьшаем DX до тех пор, пока можно будет определить новое удачное направление или пока DX не станет меньше некоторой заранее установленной допустимой величины.

Рассмотрим решение следующей задачи:

минимизировать f(X)=(X₁+1)²+X₂², начиная из точки X⁰=[2;2,8]^Т с начальным DX=[0,6;0,84]^Т. Исходное значение функции f(X⁰)=16,84.

Проводим последующий поиск типа I:

X₁¹ = 2 + 0,6 = 2,6, f(X) = 20,80 (неудача),

X₁¹ = 2 – 0,6 = 1,4, f(X) = 13,60 (успех),

X₂¹ = 2,8 + 0,84 = 3,64, f(X) = 19,00 (неудача),

X₂¹ = 2,8 – 0,84 = 1,96, f(X) = 9,50 (успех).

Исследующий поиск оказался удачным, новым базисным вектором будет точка X¹=[1,4;1,96]^Т.

Далее проводится поиск по образцу:

X₁² = 2×(1,40) – 2 =0,8,

X₂² = 2×(1,96) – 2,8 = 1,12,

f(X²) = 4,49.

Наконец, проводится исследующий поиск типа II; неудача или успех его оценивается путем сравнения исходных функций с f(X²).

X₁³ = 0,8 + 0,6 = 1,4, f(X) = 7,0l (неудача),

X₁³ = 0,8 – 0,6 = 0,2, f(X) = 2,69 (успех),

X₂³ = 1,12 + 0,84 = 1,96, f(X) = 5,28 (неудача),

X₂³ = 1,12 – 0,84 = 0,28, f(X) = 1,52 (успех).

Чтобы определить, оказался ли поиск по образцу успешным сравниваем функции f(X³) и f(X¹). Поиск по образцу является успешным f(X³)<f(X¹), значит, новой базисной точкой будет X³=[0,2;0,28]^Т. При этом старая базисная точка представлена вектором X¹=[1,4;1,96]^Т.

Затем вновь проводится поиск по образцу. Дальнейшая траектория поиска показана на рис. 3.1, из которого видно, что поиск по образцу из точки оказывается удачным и приводит в точку X⁵. Последующий поиск по образцу оказывается неудачным (f(X⁷)>f(X⁵)), хотя исследующий поиск типа II удачен. Следовательно, из точки X⁵ начинаем исследующий поиск типа I.

Порядок выполнения работы

1. Изучить метод решения задачи и составить информационную блок-схему метода.

2. Сформулировать математическую постановку задачи.

3. Выполнить ручной просчет задачи.

4. Составить программу решения задачи.

5. Запустить программу на выполнение и получить результаты.

6. Проанализировать результаты.

Содержание отчета

1. Привести математическую постановку задачи.

2. Привести результаты ручного просчета задачи.

3. Привести алгоритм метода и информационную блок-схему,

4. Привести таблицы результатов.

Варианты работ

1. Варианты методов:

1) метод Гаусса-Зейделя;

2) метод прямого поиска;

2. Варианты заданий из лабораторной работы №6.

Дата добавления: 2019-02-26; просмотров: 117; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!