Последовательный (активный) поиск

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО ДИСЦИПЛИНЕ

«МЕТОДЫ ОПТИМИЗАЦИИ И ИССЛЕДОВАНИЕ ОПЕРАЦИЙ»

 

Донецк ДонНТУ 2017

УДК 658.5.011.56 (071)

 

Методические указания к выполнению лабораторных работ по дисциплине "Мето-ды оптимизации и исследование операций ". / Составил: Ю.К. Орлов - Донецк: ДонНТУ, 2017 – 24 с.

 

 

Содержатся краткие теоретические сведения и методические рекомендации к выполнению лабораторных работ по составлению алгоритмов и программ численного решения инженерных задач методами исследования операций.

 

 

Составитель:                                                                Ю.К. Орлов, к.т.н, доц.

 

 

ЛАБОРАТОРНАЯ РАБОТА 5

Одномерный поиск

Цель работы – изучение вопросов решения задач нелинейного программирования методами одномерного поиска.

Содержание работы

Параллельный (пассивный) поиск

Поиск в данном случае базируется на предположении, что результаты измерений значений функции будут получены одновременно во всех точках.

Задача состоит в определении разумной стратегии простановки точек измерения.

Наилучшим результатом расстановки датчиков будет случай простановки датчиков относительно середины интервала на e/2 справа и слева, а новый интервал будет равен L₂=(1+e)/2. Если первоначальный интервал будет равен L₁, то L₂=( L₁+e)/2.

Пусть число датчиков равно три, тогда датчик X₂ поставляется по середине, а датчики X₁ и X₃ проставляются произвольно, но при этом должно быть выполнено условие X₃-X₁£1/2. Тогда максимальный интервал неопределенности будет L₂=1/2.

По сравнению со случаем двух датчиков получается незначительное сокращение интервала неопределенности.

Поэтому целесообразно точки проставлять парами.

Рис. 1.5 иллюстрирует случаи расстановки четырех, шести датчиков.

Из рисунка видно, что в общем случае конечный интервал неопределенности определится

.                                       (1.1)

Четные датчики проставляются на расстоянии L_n от начала интервала или последнего четного датчика, а нечетные проставляются на расстоянии e слева от них. После чего выбираем два любых датчика и проводим сокращение интервала неопределенности. Данную процедуру продолжаем до тех пор, пока внутри интервала неопределенности не останется один датчик.

Число датчиков определяем из условия достижения заданной точности т. е.

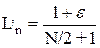
или

.                                  (1.2)

Так для того, чтобы получить интервал неопределенности L_n=10^-2, необходимо проделать приблизительно N=198 измерений (если e можно пренебречь).

Рассмотрим решение следующей задачи:

Найти max f(X)=-(X-2)²+4

при условии XÎ[0;5].

Конечный интервал неопределенности не должен превышать 1, а e=0,1.

Определим требуемое число точек измерения в соответствии с уравнением (1.2).

Выбираем N=10 .

Тогда согласно (1.1)

Определим координаты всех точек измерения

                          X² =X⁰+L_N=0,85; X¹=X² -e=0,75;

                             X⁴ =X²+L_N=1,70; X³=X⁴ -e=1,60;

                          X⁶ =X⁴+L_N=2,55; X⁵=X⁶ -e=2,45;

                          X⁸ =X⁶+L_N=3,40; X⁷=X⁸ -e=3,30;

                          X¹⁰=X⁸+L_N=4,25; X⁹=X¹⁰-e=4,15.

Выбираем любые две точки из данного интервала, пусть X³ и X⁷ значения функции в этих точках f(X³)=3,84 и f(X⁷)=2,31. Поскольку f(X³)>f(X⁷) конец интервала неопределенности перенесем в точку X⁷.

Выберем внутри оставшегося интервала точки X³ и X⁵, значения функции в них f(X³)=3,84 и f(X⁵)=3,79775. Поскольку f(X³)>f(X⁵), конец интервала неопределенности перенесем в точку X⁵.

Сравним значения функции в точках X² и X³

f(X²)=2,6775 < f(X³)=3,84.

Перенесем в точку X² начало интервала неопределенности. Внутри интервала лежат точки X³ и X⁴. Определим значение функции в них..

f(X³)=3,84 < f(X⁴)=3,91.

Следовательно переносим в точку X³ начало интервала неопределенности.

Поскольку внутри интервала осталась только одна точка, процесс поиска прекращается. В качестве экстремума выбирается точка X=X⁴=1,7.

Недостатком данного метода является его малая эффективность, так как не учитываются результаты предыдущих измерений.

Последовательный (активный) поиск

Данный метод предлагает более оптимальную стратегию поиска. Проставим внутри интервала неопределенности две точки, так чтобы максимально сократить его. Как было отмечено выше, эти точки должны быть проставлены на расстоянии e/2 справа и слева от середины интервала неопределенности.

В зависимости от результатов измерений выберем интересующий нас отрезок, длина нового интервала будет

На данном интервале проставим новые две точки, новый интервал неопределенности определиться

В общем случае интервал неопределенности после n шагов определится

L_n=2^-n/2 + (1 - 2^-n/2)e.                                   (1.3)

Таким образом, данный метод состоит в том, что интервал неопределенности делится пополам, поэтому этот метод называется методом дихотомии.

Для сравнения эффективности данного метода с пассивным поиском, определим необходимое количество измерений, которое проделать, чтобы получить L_n=10^-2.

В соответствии с (1.3)

10^-2 ³ 2 ^-n/2 + (1-2 ^-n/2)e » 2 ^-n/2.

Откуда n/2=7 или n=14.

Если исследуемая функция f(x) является дифференцируемой функцией, то метод дихотомии будет реализован следующим образом.

Исходный интервал неопределенности делим пополам и в этой точке определяется производная функции.

Если в исходной функции производная положительна  то точка экстремума находится справа от данной точки, так как последняя находится на участке возрастания функции. Поэтому в данную точку переносится начало интервала неопределенности X_H=X.

Если в исследуемой точке производная отрицательна  то точка находится на участке убывания функции, таким образом экстремум функции находится слева от данной точки. Поэтому в данную точку переносится конец интервала неопределенности X_K=X.

Если же выполняется условие  то искомая точка является экстремумом функции

После сокращения интервала процедура поиска экстремума повторяется.

Блок-схема метода представлена на рисунке 1.6.

Рассмотрим решение следующей задачи:

максимизировать f(X)=- (X-2)² +4

при условии XÎ[0;5].

Конечный интервал неопределенности не должен превышать 1, а e=0,1.

Интервал неопределенности равен

L=X_k-X_н=5-0=5.

Тогда центр интервала неопределенности определится

X=X_н+0,5*L=2,5.

Определим значение производной в этой точке.

.

Тогда переносим в данную точку конец интервала неопределенности X_k=2,5.

Новый интервал неопределенности будет

L=2,5-0=2,5>1,0.

Следовательно, процесс поиска следует продолжить.

X=X_н+0,5×L=1,25;

Таким образом в новую точку переместится начало интервала неопределенности X_н=1,25. Тогда L=2,5-1,25=1,25, что больше e, следовательно, определим новую точку

X=1,25+0,25=1,875;

Следовательно, X_н=1,875 и L=2,5-1,875=0,625<1.

Поэтому поиск прекращается.

Конечный интервал неопределенности X_н=1,875, X_к=2,5.

МЕТОД ФИБОНАЧЧИ

Данный метод использует оптимальную стратегию поиска и применяет идеи динамического программирования.

Рассмотрение задачи начинаем с конца. Предположим, что сделано n-1 измерение. Необходимо положение точки X_n.

Как было показано выше оптимальным размещением последних точек будет, если точка X_n будет сдвинута на e относительно точки X_n-1. Тогда

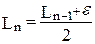                                         (1.4)

или

L_n-1=2L_n-e.                                               (1.5)

Предположим теперь, что сделано n-2 измерения. Внутри интервала L_n-2 уже существует одна точка X_n-2. Необходимо проставить точку X_n-1. Оптимальной стратегией будет, если точки X_n-1 и X_n-2 разобьют интервал неопределенности следующим образом

L_n-2=L_n-1+L_n.                                         (1.6)

Что означает, что точки внутри интервала неопределенности должны располагаться симметрично. Подставив уравнение (1.5) в (1.6) получаем

L_n-2=2L_n-e+L_n=3L_n-e.

Продолжив аналогичные рассуждения получим

L_n-3=L_n-2+L_n-1=5L_n-2e,

L_n-4=2L_n-3+L_n-2=8L_n-3e.

Просмотрев коэффициенты при L_n и e, можно сделать вывод, что они являются членами ряда Фибоначчи.

F₀=1, F₁=1, F₂=2, F₃=3, F₄=5, F₅=8, F₆=13, F₇=21, F₈=34, F₉=55, F₁₀=89, F₁₁=144 и т.д.

Числа ряда Фибоначчи определяются в соответствии с формулой

F_j=F_j-1+F_j-2.

Тогда выше приведенные формулы связи интервалов неопределенности с конечным интервалом можно переписать

L_n-1=F₂L_n-F₀e,

L_n-2=F₃L_n-F₁e,

L_n-3=F₄L_n-F₂e

или в общем случае

L_n-k=F_k+1L_n-F_k-1e.                                  (1.7)

Нас интересует начальный интервал неопределенности L₁ , т.е. n- k=1, тогда k=n-1. В соответствии с (1.7)

L₁=F_nL_n-F_n-2e.

Выразим из данного уравнения

                                   (1.8)

Если будет сделано первое измерение, то вторая точка располагается симметрично первой, и процесс поиска может быть продолжен дальше.

Задача состоит в определении местоположения первой точки. С этой целью определим величину интервала L₂ (n- k=2, а k= n-2),

L₂=F_n-1L_n-F_n-3e.

Подставим в данное выражение вместо L_n его значение из (1.8)

Учитывая, что F_n-1=F_n-2+F_n-3, а F_n=F_n-1+F_n-2, получим

.

Принимая во внимание, что

F_n-2²-F_n-1F_n-3=(–1)ⁿ,

получаем

.                              (1.9)

Тогда первые два измерения будут проделаны в точках

X₁=X_k-L₂,

X₂=X_н-L_2.

Как видно из формулы (1.9) первый отсчет зависит от числа экспериментов и заданной точности измерения. Но число экспериментов заранее не известно, а точность решения может измеряться в процессе измерения, что приводит к необходимости повторения решения. В этом недостаток данного метода.

Оценим требуемое число экспериментов. Для этого положим, что

где 2e показывает, что внутри этого интервала можно проставить только одно измерение.

Тогда получаем

L₁+F_n-2e £ 2eF_n

или

L₁ £ (2F_n-F_n-2)e,

где 2F_n-F_n-2=F_n+F_n-1=F_n+1.

Следовательно

Так, если e=0,01, L₁=1, то

Этому условию удовлетворяет F₁₁=144, тогда n=10.

Блок-схема представлена на рис. 1.7.

Рассмотрим решение следующей задачи

максимизировать f(X) = -(X-2)²+4

при условии ХÎ[0,5], e=0.5.

Определим требуемое число измерений

В соответствии с рядом Фибоначчи F₆=13>10, тогда n=5.

Следовательно

Тогда

X₁=5–3,06=1,94,

X₂=0+3,06=3,06.

Значение функции в этих точках f(X₁)=3,9964 и f(X₂)=2,8764.

Поскольку f(X₁)>f(X₂) и n=5, то переходим к сокращению интервала

X_k=X₂=3,06; X₂=X₁=1,94; f(X₂)=3,9964;

X₁=0+3,06–1,94=1,12; n=4;

f(X₁)=3,2256.

В данном случае f(X₂)>f(X₁), следовательно, переносим начало интервала неопределенности

X_н=X₁=1,12; X₁=X₂=1,94; f(X₁)=3,9964;

X₂=1,12+3,06–1,94=2,24,12; n=3;

f(X₂)=3,9424.

Вновь получаем f(X₁)>f(X₂), тогда

X_k=X₂=2,24; X₂=X₁=1,94; f(X₂)=3,9964;

X₁=1,12+2,24–1,94=1,44; n=2;

f(X₁)=3,7084.

Поскольку f(X₂)>f(X₁) и n=2 процесс решения завершается.

Х_н=1,44; Х_k=2,24; =1,94; f( )=3,9964.

Метод золотого сечения

В основу метода положено, как и в методе Фибоначчи, уравнение (1.6). Кроме этого требуется, чтобы отношение предыдущего интервала к последующему было постоянным

.                                (1.10)

Разделив уравнение (1.6) на L_n-1, получаем

или

Таким образом, приходим к уравнению

t²-t-1=0.

Решив уравнение, получаем t=1,618.

Тогда координаты первых точек определяют

где L=Х_k–Х_н.

После сравнения f(X₁) и f(X₂) переходим к сокращению интервала неопределенности.

Первое измерение не изменяет интервал неопределенности, сокращение начинается со второго измерения, тогда после n шагов интервал неопределенности будет L_n=1/t^n-1.

Метод золотого сечения по оптимальности не уступает методу Фибоначчи, но свободен от его недостатков.

Блок-схема метода представлена на рис. 1.8.

Рассмотрим следующий пример

максимизировать f(X)=-(X-2)²+4

при условии ХÎ[0,5], L_n=1.

Исходный интервал неопределенности будет равен

L = X_к - X_н = 5 – 0 = 5.

Тогда

Следовательно

X₁ = 5 – 3,09 = 1,91; f(X₁) = 3,9919;

X₂ = 0 + 3,09 = 3,09; f(X₂) = 2,8119.

Таким образом f(X₁)>f(X₂), следовательно

X_к = X₂ = 3,09; X₂ = X₁ = 1,91; f(X₂) = 3,9919;

L = X_к – X_н = 3,09.

Поскольку L>L_n, определяем координаты точки X₁

f(X₁) = 3,2276.

Теперь f(X₁)<f(X₂), следовательно

X_н = X₁ = 1,18; X₁ = X₂ = 1,91; f(X₁) = 3,9919;

L = X_к – X_н = 1,91.

Так как L>L_n, определяем координаты точки X₂

f(X₂) = 3,8704.

В данном случае получаем f(X₁)>f(X₂), таким образом

X_к = X₂ = 2,36; X₂ = X₁ =1,91; f(X₂) = 3,9919;

L = X_к – X_н = 1,18.

Вновь L>L_n, следовательно поиск экстремума продолжается

f(X₁) = 3,8631.

Теперь получаем f(X₁)<f(X₂), следовательно

X_н = X₁ = 1,63; X₁ = X₂ = 1,91; f(X₁) = 3,9919;

L = X_к – X_н = 0,73.

Поскольку L<L_n, процесс вычислений заканчивается, в качестве экстремума выбирается точка =X₁=1,91, в которой f( )=3,9919.

Метод касательных

Данный метод используется для поиска экстремума функции f(X), которая является дифференцируемой и вогнутой.

Поиск экстремума состоит в следующем.

Выбираем две точки, пусть X₁=X_н, а X₂=X_k. В этих точках проводим касательные к функции.

,                          (1.11)

.

Находим точку пересечения этих касательных, для чего приравниваем Y₁=Y₂, тогда

,

откуда

              (1.12)

В полученной анализируем поведение функции, для этого вычисляем производную в этой точке. Если , то функция возрастает справа от точки, поэтому перенесем в эту точку начало интервала неопределенности Х_н=Х, если же , то экстремум лежит слева от точки, поэтому переносится конец интервала неопределенности Х_k=Х. А в случае равенства нулю производной ( ) экстремум находится в данной точке ( =X).

Если в результате проверки производной максимум функции не будет найден, процесс поиска повторяется. При решении практических задач точное определение экстремума функции затруднительно, поэтому в качестве дополнительного условия остановки процесса используется условие

½X_k-X_н½£e.

Блок-схема метода приведена на рисунке 1.9.

Рассмотрим решение следующей задачи:

максимизировать f(X)=-(X-2)²+4

при условии XÎ[0,5], e=1.

В соответствии с (1.11) уравнения касательных запишутся

У₁ = 0 + 4×(X - 0) = 4X;

У₂ = -5 + (-6)(X - 5) = -6X + 25.

Приравнивая правые части уравнения, получим

4Х = -6Х+25.

Откуда Х=2.5. Поскольку =1<0, переносим конец интервала неопределенности Х_k=Х=2,5.

Интервал неопределенности L=2,5.

Проводим касательную в точке X₂=X_k

Y₂ = 3,75 - (X - 2,5) = -X + 6,25.

Найдем точку пересечения касательных

4Х = -Х + 6,25 или Х = 1,25.

В данной точке =1,5>0, поэтому переносим начало интервала неопределенности Х_н=Х=1,25. Интервал неопределенности L=1,25>1, поэтому строится новая касательная в точке X₁.

Y₁ = 3,4375 + 1,5(X + 1,25) = 1,5X + 1,5625.

Найдем точку пересечения касательных

1,5Х + 1,15625 = -Х + 6,25; Х = 1,875;

В этой точке =0,25>0, отсюда Х_н=Х=1,875. Интервал неопределенности L=0,625<1, следовательно, поиск можно прекратить. В качестве экстремума будет выбрана точка =X_н=1,875, поскольку f(X_н)=3,9844>f(X_k)=3,75.

Порядок выполнения работы

1. Изучить метод решения задачи и составить информационную блок-схему метода.

2. Выполнить ручной просчет задачи.

3. Составить программу решения задачи.

4. Запустить программу на выполнение и получить результаты.

5. Проанализировать результаты.

Содержание отчета

1. Привести математическую постановку задачи.

2. Привести результаты ручного просчета задачи.

3. Привести алгоритм метода и информационную блок-схему,

4. Привести таблицы результатов.

Варианты работ

1.Варианты методов:

1) параллельный (пассивный) поиск;

2) метод дихотомии (дифференцируемые функции);

3) последовательный (активный) поиск (без производных);

4) метод Фибоначчи;

5) метод золотого сечения;

6) метод касательных.

 

2. Варианты заданий:

1. max f(x) = –2x²+4x+5, хÎ[0;5], e =0.1;

2. max f(x) = –x⁴+x²+3x–6, хÎ[1;4], e =0.2;

3. max f(x) = sin x, хÎ[p/4;5p/4], e =0.3;

4. max f(x) = –5x²–5x+3, хÎ[–2;6], e =0.2;

5. min f(x) = 4x²–2x+5, хÎ[–1;4], e =0.1;

6. min f(x) = 2x⁴+3x²+x+3, хÎ[–2;3], e =0.2;

7. min f(x) = 3x²+x–3, хÎ[–3;1], e =0.1;

8. min f(x) = x²+4x+4, хÎ[–3;2], e =0.1;

9. max f(x) = cos x, хÎ[3p/4;7p/2], e =0.2;

10. max f(x) = –5x²–3x+4, хÎ[–3;2], e =0.1.

 

ЛАБОРАТОРНАЯ РАБОТА 6

Градиентные методы

Цель работы – изучение вопросов решения задач нелинейного программирования с помощью градиентных методом.

Содержание работы

Поскольку градиент целевой функции f(X) в любой точке Х есть вектор в направлении наибольшего локального увеличения f(X), можно выбрать это направление за направление движения из точки X^k в точку X^k+1 . Тогда уравнение движения запишется так:

                          (2.1)

где l – величина шага;

Ñf(X^k) – градиент функции в точке X^k.

В зависимости от выбора l можно прийти к различным процедурам поиска экстремума.

---

Дата добавления: 2019-02-26; просмотров: 347; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!