Равномерный градиентный поиск
В данном случае поиск можно начать из некоторой произвольной точки X0, величина шага остается постоянной. Тогда в качестве уравнения движения выбирается уравнение (2.1). Процесс определения новой точки продолжается до тех пор, пока направление не изменится на противоположное, т. е. экстремум функции уже пройден (  ), или пока не будет найдена точка экстремума (Ñf(Xk+1)=0).
), или пока не будет найдена точка экстремума (Ñf(Xk+1)=0).
Недостатком этого метода является плохая его сходимость, поскольку в процессе движения поведение функции не принимается во внимание, и шаг остается все время постоянным.
Рассмотрим следующую задачу:
найти mаx f(X) = 1 – X12 – 2X22.
В качестве начальной точки можно выбрать X0=[2;3]т, значение функции в которой f(X0)=-21. Величина шага l=0,1. Тогда градиент можно вычислить следующим образом:
 .
.
Согласно формуле (2.1) новый вектор
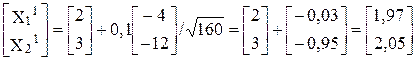 .
.
В этой точке значение функции f(X1)=–11,29, градиент Ñf(X1)=[–3,94;–8,2]т. Поскольку знаки проекций градиента остались прежними, процесс необходимо продолжить.
Пропорциональный градиентный поиск
Чтобы устранить выше отмеченный недостаток, выберем величину шага пропорциональной модулю градиента:
lk=l0║Ñf(Xk)║.
В этом случае по мере приближения к точке экстремума шаг будет уменьшаться. Тогда уравнение (2.1) преобразуется следующим образом:
 (2.2)
(2.2)
где l0 – некоторый скаляр.
Поскольку один шаг в направлении градиента в общем случае не приводит в точку экстремума f(X), формула (2.2) должна применяться несколько раз, до тех пор пока не будет достигнут максимум.
|
|
|
Обычно в качестве критерия остановки выбирается

или, если f(Xk+1)®0, (2.3)
½f(Xk+1)-f(Xk)½£ e ,
и

или, если Xjk ®0, (2.4)
½Xjk+1-Xjk½£e.
Применим изложенный метод для поиска максимума f(X)=1-X12-2X22. В качестве начальной точки выберем X0=[2;3]T, значение функции в которой f(X0)=–21; величина шага l0=0,1, градиент Ñf(Xk)=[–2X1k;–2k]Т=[–4;–12]Т.
Тогда согласно формуле (2.2) координаты новой точки
 .
.
Значение функции в этой точке f(X1)=–8,04. Если сравнить данный результат с результатом, полученном при использовании равномерного поиска при том же значении l0, следует отметить улучшение функции. Процесс решения следует продолжить, пока не выполнятся условия (2.3) или (2.4).
Метод наискорейшего подъема
Применение данного метода было рассмотрено еще французским математиком Коши. В этом случае в качестве уравнения движения выбирается уравнение (2.2). Величина шага определяется из условия достижения экстремума функции вдоль выбранного направления. Согласно формуле (2.2)
|
|
|
f(Xk+1)=f(Xk+lÑf(Xk))=j(l).
Таким образом, мы переходим от поиска экстремума функции со многими переменными к оптимизации функции с одной переменной. При этом могут быть использованы любые методы одномерного поиска.
Описанную процедуру необходимо продолжать до тех пор, пока не будет найдено оптимальное решение.
В качестве примера можно рассмотреть задачу:
максимизировать f(X)=1-X12-X22.
За начальную точку выбираем X0=[2;3]T, в которой значение функции f(X0)=-21.
В соответствии с изложенным выше алгоритмом
Xk+1=Xk+l*kÑf(Xk),
где  .
.
Тогда новый вектор X1 можно вычислить по формуле
 .
.
Поскольку целевая функция весьма проста, для наглядности можно определить l*0 путем максимизации f(X1) по l*, используя аналитические методы вместо процедуры поиска:
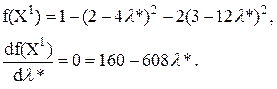
или l*0=0,263.
Итак, на этом шаге X1=[0,948;–0,156]т, а f(X1)=0,053.
Описанную процедуру необходимо продолжать до тех пор, пока не будет достигнута заданная точность решения или пока градиент не обратится в ноль.
Порядок выполнения работы
1. Изучить метод решения задачи и составить информационную блок-схему метода.
2. Выполнить ручной просчет задачи.
3. Составить программу решения задачи.
|
|
|
4. Запустить программу на выполнение и получить результаты.
5. Проанализировать результаты.
Содержание отчета
1. Привести математическую постановку задачи.
2. Привести результаты ручного просчета задачи.
3. Привести алгоритм метода и информационную блок-схему,
4. Привести таблицы результатов.
Варианты работ
1. Варианты методов:
1. равномерный градиентный поиск;
2. пропорциональный градиентный поиск;
3. метод наискорейшего подъема Коши;
2. Варианты заданий:
1. max f(x) = –4x12–2x22+3x1x2, e =0.1;
2. max f(x) = –x12–4x22+2x1+3x1x2, e =0.5;
3. max f(x) = –5x12–x22–5x1x2+2x1, e =0.3;
4. min f(x) = 2x12+3x22+x1+5x2, e =0.2;
5. max f(x) = –x12+2x1x2–5x22–4x1, e =0.1;
6. max f(x) = –6x12–10x22–5x1x2+4x2, e =0.5;
7. min f(x) = 5x12+6x22–2x1–4x2, e =0.6;
8. min f(x) = x12+3x22+2x1x2+4x2, e =0.1;
9. max f(x) = –x12+3x1–2x22, e =0.2;
10. min f(x) = 5x12–3x2+4x22+x1x2, e =0.3;
11. max f(x) = –6x12+2x1x2–x22, e =0.3;
12. max f(x) = –x12+6x1x2–4x22, e =0.1;
13. max f(x) = –3x12+x1x2–2x22, e =0.2;
14. max f(x) = –x12+2x1x2–4x22, e =0.1;
15. min f(x) = 3x12+8x1–x1x2+2x22, e =0.1;
16. min f(x) = 2x12+8x1x2+x22–x2, e =0.2;
17. max f(x) = –3x12+4x1x2–5x22+x2, e =0.1.
ЛАБОРАТОРНАЯ РАБОТА 7
Дата добавления: 2019-02-26; просмотров: 158; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
