Системы линейных алгебраических уравнений. Правило Крамера

Система трех линейных уравнений с тремя неизвестными  имеет вид 

  (4)

где  - коэффициенты системы, 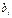- свободные члены .

Определитель третьего порядка Δ, составленный из коэффициентов при неизвестных, называется определителем системы.

Теорема. (Правило Крамера):

Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = D _i / D , где

D = det A , а D _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i .

D _i =

Теорема Кронекера-Капелли . Условия существования единственного решения и бесконечного множества решений.

Теорема Кронекера – Капелли.

 

Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA^*.

 

Очевидно, что система (1) может быть записана в виде:

x₁ 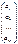 + x₂ + … + x_n

 

 

Доказательство.

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А^* не изменяют ранга.

2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

 

Пример. Определить совместность системы линейных уравнений:

 

A =

 

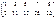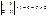~ .    RgA = 2.

A* =      RgA* = 3.

                   Система несовместна.

Однородная система линейных уравнений. Свойства ее решений.

Фундаментальная система решений однородной системы линейных уравнений.

1. Системы линейных однородных уравнений.

Система т линейных уравнений с п неизвестными называется системой линейных однородных уравнений, если все их свободные члены равны нулю, т.е.

                    (9)

                   Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое решение (0; 0; …; 0).

                   Если в системе (9) т=п, а ее определитель отличен от нуля, то такая система имеет только нулевое решение. Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю.

                   Другими словами: система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при r ( A ) < n.

                   Обозначим решение системы (9)  в виде строки .

 Решения системы линейных однородных уравнений обладает следующими свойствами:

                   1. Если строка  - решение системы (9), то и строка  - также решение этой системы.

                   2. Если строки  и  - решения системы (9), то при любых с₁ и с₂ их линейная комбинация  - также решение данной системы.

                   Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.

                   2. Фундаментальная система решений.

Система линейно независимых решений  называется фундаментальной, если каждое решение системы (9) является линейной комбинацией решений .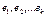

                   Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (9) меньше числа переменных п, то всякая фундаментальная система решений системы (9) состоит из п-r решений.

                   Поэтому общее решение системы (9) линейных однородных уравнений имеет вид:

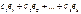,                        (10)

где  - любая фундаментальная система решений,  - произвольные числа и .

                   Можно показать, что общее решение системы т однородных уравнений с п переменными

равно сумме общего решения соответствующей ей системы линейных однородных уравнений (9) и произвольного частного решения этой системы (9).

5. Неоднородная система линейных уравнений. Свойства ее решений. Связь решений неоднородной системы линейных уравнений и соответствующей однородной системы. системы линейных неоднородных уравнений

Рассмотрим систему неоднородных уравнений

     (13)

Пусть . Пусть  – решение этой системы, т.е.

(14)

Вычитая из (13) выражение (14), получаем

.

Т.о.,  является решением соответствующего однородного уравнения.

Пусть  – фундаментальная система решений однородного уравнения. Тогда любое  может быть представлено в виде:

.

Тогда получаем

(15)

Если  – частное решение уравнения (13), то формулы (15) дают общее решение. Из (15) следует теорема.

Теорема 7. Общее решение СЛНУ (13) представляется в виде суммы произвольного частного решения этой системы и общего решения соответствующей ей однородной системы.

Следствие 1. Разность двух произвольных решений СЛНУ является решением соответствующей СЛОУ.

Следствие 2. Сумма любого частного решения СЛНУ с любым частным решением соответствующей СЛОУ дает частное решение СЛНУ.

Замечание. В формуле (7) вектор  – частное решение СЛНУ, а вектора  – частные решения СЛОУ.

 

 

---

Дата добавления: 2019-02-22; просмотров: 171; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!