Линейно зависимые и линейно независимые системы строк (столбцов) матрицы, их свойства.
Линейная независимость строк матрицы
Дана матрица 
размера 
Обозначим строки матрицы следующим образом:
Две строки называются равными, если равны их соответствующие элементы. 
.
Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно:
.
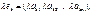
Определение. Строка 
называется линейной комбинацией строк 
матрицы, если она равна сумме произведений этих строк на произвольные действительные числа 
(любые числа):
.
Определение. Строки матрицы 
называются линейно зависимыми, если существует такие числа 
, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
, где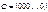 
. (1.1)
Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.
Определение. Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты 
, то строки называются линейно независимыми.
Свойства:1. 
линейно зависимо2.M линейно независимо 
M' линейно независимо для всех 
M линейно зависимо 
M' линейно зависимо для всех 
Ранг матрицы, его свойства.
Теорема о ранге матрицы . Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы).
Свойства:
Теорема (о базисном миноре): Пусть 
— базисный минор матрицы A, тогда:
1.базисные строки и базисные столбцы линейно независимы;
|
|
|
2.любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).
Следствия:
Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.
Если A — квадратная матрица, и 
, то строки и столбцы этой матрицы линейно зависимы.
Пусть 
, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.
Вычисление ранга матрицы с помощью элементарных преобразований. Ранг ступенчатой матрицы
Элементарные преобразования матрицы:
1.Отбрасывание нулевой строки (столбца).
2.Умножение всех элементов строки (столбца) на число 
.
3.Изменение порядка строк (столбцов) матрицы.
4.Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
5.Транспонирование матрицы.
Определение. Матрица , полученная из матрицы 
при помощи элементарных преобразований, называется эквивалентной и обозначается А 
В.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
|
|
|
Матрица 
называется ступенчатой если она имеет вид:
, где 
, 
, 
.
Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк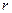 
, т.к. имеется минор 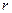-го порядка, не равный нулю:
.
Ранг ступенчатой матрицы равен числу ненулевых строк.
Пусть в ступенчатой матрице имеется 
ненулевых строк. Тогда каждый минор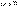 
-го и высшего порядка содержит нулевые строки (хотя бы одну) и потому равен нулю. Но имеется хотя бы один минор -го порядка отличный от нуля: наверняка треугольный минор не равен нулю, главную диагональ которого образуют первые ненулевые элементы всех 
ненулевых строк. Действительно, такой минор равен произведению элементов главной диагонали и поэтому не равен нулю. Значит 
.
Дата добавления: 2019-02-22; просмотров: 827; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!