Тема: «Логарифмы и их свойства»
Практическое занятие №1
Тема: «Иррациональные уравнения»
Цели работы: закрепить навыки решения иррациональных уравнений.
Краткое содержание материала
Уравнения, в которых переменная содержится под знаком корня называются иррациональными.
Иррациональные уравнения часто получаются при решении различных задач. Решение иррациональных уравнений основано на следующем свойстве: при возведении обеих частей уравнения в натуральную степень получается уравнение – следствие данного.
При возведении обеих частей уравнения в натуральную степень может получиться уравнение не равносильное данному.
При возведении обеих частей уравнения в натуральную степень возможно появление посторонних корней. Поэтому необходимо выполнить проверку, подставив найденные корни в исходное уравнение.
Примеры:
1. 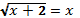 возведем обе части уравнения в квадрат
возведем обе части уравнения в квадрат
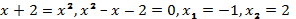
Проверка:1) 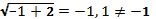 посторонний корень
посторонний корень
2) 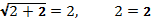
Ответ:2
2. 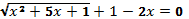
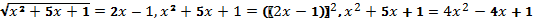
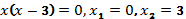
Проверка: 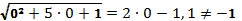
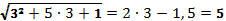
Ответ:3
Задания для самостоятельной работы:
Решите уравнения:
1. 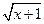 = 5
= 5
2. 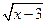 = 4
= 4
3. 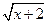 =
= 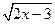
4. 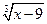 = - 3
= - 3
5. 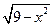 =
= 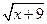
6. 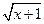 = х -5
= х -5
7. х + 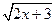 = 6
= 6
8.  =
= 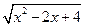
9. х = 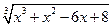
10. 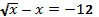
11. 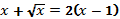
12. 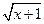 ·
· 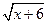 = 6
= 6
Практическое занятие №2
Тема: «Показательные уравнения и неравенства»
Цели работы: сформировать умения и навыки решения показательных уравнений и неравенств
Краткое содержание материала:
1.Уравнения, в которых переменная содержится в показателе степени называются показательными
Простейшее показательное уравнение 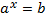 , при
, при 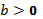 уравнение имеет один корень, при
уравнение имеет один корень, при 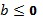 нет корней
нет корней
Решение показательных уравнений часто сводится к решению уравнения 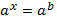 , где
, где 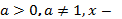 неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием (
неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием ( 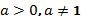 ) равны тогда и только тогда, когда равны их показатели.
) равны тогда и только тогда, когда равны их показатели.
2.Неравенство, содержащее переменную в показателе степени, называется показательным
Решение показательных неравенств вида 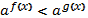 (где
(где 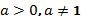 ) основано на следующих утверждениях:
) основано на следующих утверждениях:
Если а>1, то неравенства 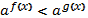 и
и 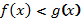 равносильны;
равносильны;
если 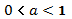 то неравенства
то неравенства 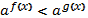 и
и 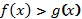 равносильны. Это следует из того, что при а>1,показательная функция возрастает, а при
равносильны. Это следует из того, что при а>1,показательная функция возрастает, а при 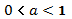 , убывает
, убывает
Примеры
Решите уравнения
1. 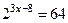 , т.к.
, т.к. 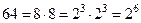 , то
, то 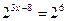 , мы привели обе части уравнения к одинаковому основанию, а так как степени равны, равны их основания, то равны и показатели степеней, т.е
, мы привели обе части уравнения к одинаковому основанию, а так как степени равны, равны их основания, то равны и показатели степеней, т.е 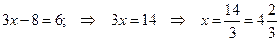
Показатель степени может быть любым числом, поэтому проверку делать не надо.
Ответ: 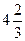
2. 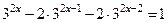 используя свойства степени, имеем
используя свойства степени, имеем 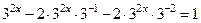 в левой части каждое слагаемое содержит общий множитель
в левой части каждое слагаемое содержит общий множитель 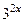 . Вынесем
. Вынесем 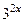 за скобки, получим:
за скобки, получим: 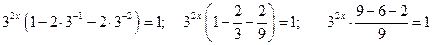
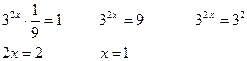
Ответ: 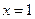 . Этот метод называется – метод вынесения общего множителя за скобки
. Этот метод называется – метод вынесения общего множителя за скобки
3. 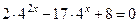 так как
так как 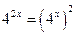 , то уравнение
, то уравнение 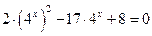 представляет квадратное уравнение относительно
представляет квадратное уравнение относительно 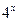 . Пусть
. Пусть 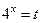 , тогда
, тогда 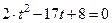 решаем квадратное уравнение относительно переменной t.
решаем квадратное уравнение относительно переменной t.
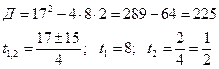
Подставим значения t в равенство 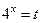
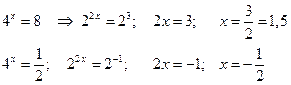
Ответ: 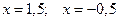 .
.
4. Решите неравенство
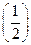
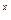 >
> 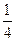 ;
; 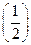
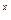 >
> 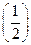
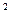 ; а =
; а = 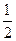 , так как 0< а< 1, то
, так как 0< а< 1, то 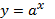 убывает, а значит х < 2
убывает, а значит х < 2
Ответ: (- 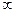 ; 2)
; 2)
Задания для самостоятельной работы
1 вариант
Решить уравнения:
1) 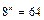 ;
;
2) 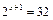 ;
;
3) 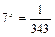 ;
;
4) 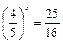 ;
;
5) 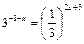 ;
;
6) 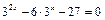 ;
;
Решить неравенства:
1) 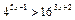 ;
;
2) 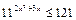 ;
;
3) 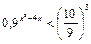 ;
;
Практическое занятие №3
Тема: «Логарифмы и их свойства»
Цели работы: сформировать умения и навыки преобразовывать выражения, используя определение логарифма и свойства логарифма.
Краткое содержание материала:
Логарифмом положительного числа b по основанию а , где a>0, а 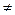 1 называется показатель степени, в которую нужно возвести основание а , чтобы получить число b.
1 называется показатель степени, в которую нужно возвести основание а , чтобы получить число b.
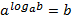 - основное логарифмическое тождество
- основное логарифмическое тождество
Действие нахождения логарифма числа называют логарифмированием.
Свойства:
1. log 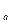 1=0
1=0
2. log 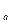 a =1
a =1
3. log 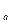 x y = log
x y = log 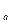 x + log
x + log 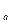 y
y
4. log 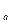
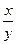 = log
= log 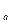 x - log
x - log 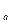 y
y
5. log 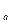 x
x 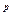 = p log
= p log 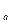 x
x
Задания для самостоятельной работы
1 вариант
Вычислите
1. log 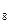 64
64
2. log 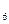 1
1
3. log 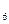
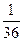
4. log 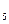 5
5
5. 10 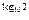
6. log 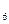 2 + log
2 + log 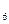 3
3
7. lg 25 + lg 4
8. log 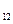 2 + log
2 + log 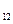 72
72
9. log 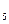 75 - log
75 - log 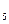 3
3
10. log 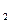 7 - log
7 - log 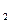
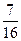
2 вариант
Вычислите
1. log 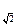 1
1
2. lg 0,01
3. log 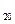 5 + log
5 + log 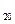 4
4
4. 5 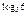
5. 2 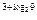
6. lg 0,5 + lg2
7. log 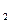 15 - log
15 - log 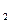 30
30
8. log 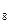
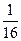 - log
- log 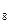 32
32
9. log 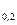 40 - log
40 - log 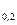 8
8
Практическое занятие №4
Дата добавления: 2019-02-22; просмотров: 176; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
