Теорема 5. 1 (Кнастер-Тарський-Кліні)
Нехай D – ω-область,  :D®D – неперервне відображення, задане на цій області. Тоді існує найменша нерухома точка
:D®D – неперервне відображення, задане на цій області. Тоді існує найменша нерухома точка  , яка позначається
, яка позначається  та для якої справедлива наступна формула:
та для якої справедлива наступна формула:
 (^) (^)
| (КТК) |
де  ,
,  , iÎw.
, iÎw.
Доведення теореми складається з трьох тверджень:
- Доведення факту, що множина {
 } iÎw є ланцюг (тому її супремум
} iÎw є ланцюг (тому її супремум 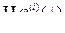 існує).
існує). - Доведення того, що
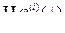 є нерухомою точкою φ.
є нерухомою точкою φ. - Доведення, що
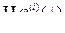 є найменшою з нерухомих точок φ.
є найменшою з нерухомих точок φ.
Почнемо з першого твердження. Розглянемо послідовність  .
.
Доведемо методом математичної індукції, що це – ланцюг.
База індукції: Оскільки ^ – найменший елемент D, то  .
.
Індуктивний крок. Треба довести, що з  випливає
випливає  . Дійсно, за монотонністю φ маємо
. Дійсно, за монотонністю φ маємо
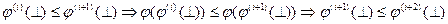 .
.
Отже  – ланцюг.
– ланцюг.
Перейдемо до другого твердження. За неперервністю  :
:
 .
.
Остання рівність випливає з того, що  , а найменший елемент не впливає на супремум. Отже,
, а найменший елемент не впливає на супремум. Отже, 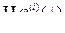 – нерухома точка φ.
– нерухома точка φ.
Доведемо тепер останнє твердження, що 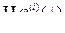 – найменша нерухома точка (ННТ).
– найменша нерухома точка (ННТ).
Нехай b також нерухома точка, тобто  . Маємо, що
. Маємо, що 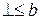 . За монотонністю φ
. За монотонністю φ  . Аналогічно,
. Аналогічно,  для всіх iÎw. Тому
для всіх iÎw. Тому  . Отже,
. Отже, 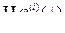 – найменша з нерухомих точок.▄
– найменша з нерухомих точок.▄
Теорема 5. 2 (структура множини нерухомих точок)
Нехай D –  -область,
-область,  – неперервне відображення на D. Тоді множина нерухомих точок Y=
– неперервне відображення на D. Тоді множина нерухомих точок Y=  –
–  -область
-область
Доведення.
Доведемо, що виконуються три умови визначення  -області.
-області.
|
|
|
1. Частковий порядок на множині нерухомих точок отримуємо як звуження часткового порядку на D: 
2. Найменшим елементом в Y є елемент  (за теоремою Кнастера-Тарського-Кліні)
(за теоремою Кнастера-Тарського-Кліні)
3. Доведемо повноту. Розглянемо ланцюг  елементів Y. Покажемо, що границя ланцюга є нерухомою точкою, тобто
елементів Y. Покажемо, що границя ланцюга є нерухомою точкою, тобто  . Дійсно,
. Дійсно,
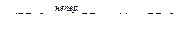 . Тобто
. Тобто  – нерухома точка.▄
– нерухома точка.▄
Перш ніж рухатись далі у вивченні властивостей оператора найменшої нерухомої точки, доведемо важливу лему.
Лема 5.2 Якщо множина 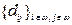 Í D впорядкована за обома індексами, тобто "iÎw"jÎw (d ij£d i(j+1)& d ij£d(i+1)j), то
Í D впорядкована за обома індексами, тобто "iÎw"jÎw (d ij£d i(j+1)& d ij£d(i+1)j), то
 =
=  .
.
Доведення.
Попередньо необхідно показати, що множини, які розглядаються під супремумами, є ланцюгами (тобто {  }j Î w, {
}j Î w, {  }j Î w, {
}j Î w, {  } k Î w – ланцюги). Це випливає з вибору множини
} k Î w – ланцюги). Це випливає з вибору множини  .
.
Метод доведення леми полягає в тому, що ми покажемо, що множини мажорант усіх ланцюгів співпадають. Звідси буде випливати рівність границь (бо вони є найменшими з мажорант).
Нехай  – мажоранта ланцюга {
– мажоранта ланцюга {  }j Î w. Звідси
}j Î w. Звідси  – мажоранта
– мажоранта  для всіх
для всіх  та для всіх
та для всіх  , а отже
, а отже  – мажоранта для
– мажоранта для  для всіх
для всіх  , тобто
, тобто  – мажоранта для ланцюга {
– мажоранта для ланцюга {  }j Î w. Аналогічно
}j Î w. Аналогічно  – мажоранта для ланцюга {
– мажоранта для ланцюга {  } k Î w.
} k Î w.
Залишилося продемонструвати, що якщо  – мажоранта для {
– мажоранта для {  } k Î w, то
} k Î w, то  – мажоранта для {
– мажоранта для {  }j Î w. Дійсно, для будь якого елемента dij існує k (зокрема, k=max(i, j)), що dij£ dkk. Тому
}j Î w. Дійсно, для будь якого елемента dij існує k (зокрема, k=max(i, j)), що dij£ dkk. Тому  – мажоранта для {
– мажоранта для {  }j Î w. ▄
}j Î w. ▄
|
|
|
5.5 Конструювання похідних  -областей
-областей
В програмуванні поруч з базовими типами даних часто використовуються похідні (структуровані) дані. Для дослідження рівнянь над похідними даними доречно розглянути побудову похідних  -областей з базових областей. Найпростішим методом побудови є об’єднання областей.
-областей з базових областей. Найпростішим методом побудови є об’єднання областей.
Розмічене об’єднання  -областей
-областей
Не втрачаючи загальності, розглянемо випадок двох областей. Нехай D1 та D2 –  -області. Будемо індексувати відповідні поняття наступним чином: £D1, ^D1,
-області. Будемо індексувати відповідні поняття наступним чином: £D1, ^D1,  – для першої області, £D2, ^D2,
– для першої області, £D2, ^D2,  – для другої області. Нехай також D1 та D2 не перетинаються. Будуємо нову множину D = D1ÈD2È{^}, де ^ – новий елемент, що не належить ні D1, ні D2.
– для другої області. Нехай також D1 та D2 не перетинаються. Будуємо нову множину D = D1ÈD2È{^}, де ^ – новий елемент, що не належить ні D1, ні D2.
На множині D вводимо частковий порядок наступним чином:
£ D = £D1È £D2 È{(^,^)} È {(^, d1) | d1Î D1}È {(^, d2) | d2Î D2}
Іншими словами, новий частковий порядок є об’єднанням часткових порядків на D1 та D2, і крім того елемент ^ визначено найменшим елементом в D.
Неважко довести, що колапсу так побудованого відношення часткового порядку не буде. Повнота D відносно порядку £ D випливає з його розміченості (множини D1 та D2 не перетинаються, тому ланцюг обов’язково складається з елементів однієї множини крім, можливо, ^).
|
|
|
Лема 5.3 Розмічене об’єднання  -областей є
-областей є  -областю.
-областю.
Декартовий добуток  -областей
-областей
Нехай D1 та D2 –  -області. Побудуємо
-області. Побудуємо  -область для D = D1´D2.
-область для D = D1´D2.
Задамо частковий порядок на D покоординатно:
(d1, d2) £ D (d1¢, d2¢)  (d1 £ D1 d1¢) & (d2) £ D2 d2¢)
(d1 £ D1 d1¢) & (d2) £ D2 d2¢)
Неважко довести, що так визначене відношення є частковим порядком.
Найменшим елементом D буде елемент (^D1, ^D2).
Доведемо повноту D відносно введеного відношення. Нехай {(d1 i, d2 i)}iÎw – ланцюг в D. Це можна зробити, показавши, що  =(
=(  ,
,  ). Для цього слід показати, що {d1 i}iÎw та {d2 i}jÎw – ланцюги відповідно в D1 та D2, та що елемент (
). Для цього слід показати, що {d1 i}iÎw та {d2 i}jÎw – ланцюги відповідно в D1 та D2, та що елемент (  ,
,  ) є, по-перше, мажорантою елементів (d1 i, d2 i), iÎw, та по-друге, є найменшою мажорантою.
) є, по-перше, мажорантою елементів (d1 i, d2 i), iÎw, та по-друге, є найменшою мажорантою.
Тут підемо трошки іншим шляхом. А саме, покажемо справедливість більш простих співвідношень:  =
=  та
та  =
=  , де d 1ÎD 1, d 2ÎD 2. Далі позначимо dij=(d1 i, d2 j), де
, де d 1ÎD 1, d 2ÎD 2. Далі позначимо dij=(d1 i, d2 j), де  . Множина елементів dij впорядкована за обома індексами, тому згідно леми 5.2
. Множина елементів dij впорядкована за обома індексами, тому згідно леми 5.2
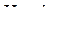 =
=  =
=  =
=  = (
= (  ,
,  ).
).
Оскільки  та
та  існують, то існує і супремум
існують, то існує і супремум 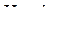 .
.
Отже, доведено наступне твердження.
Лема 5. 4 Декартовий добуток  -областей є
-областей є  -областю.
-областю.
|
|
|
Лема 5.5 Нехай D1 та D2 –  -області. Тоді відображення
-області. Тоді відображення 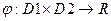 неперервне тоді і тільки тоді, коли воно неперервне за кожним аргументом.
неперервне тоді і тільки тоді, коли воно неперервне за кожним аргументом.
Доведення
Необхідність. Нехай відображення 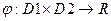 неперервне на множині D = D1´D2. Це означає, що для довільного ланцюга
неперервне на множині D = D1´D2. Це означає, що для довільного ланцюга  з D = D1´D2 маємо, що
з D = D1´D2 маємо, що  .
.
Щоб довести неперервність за першим аргументом розглянемо ланцюг  , у елементів якого другий компонент дорівнює
, у елементів якого другий компонент дорівнює  . Звідси випливає, що
. Звідси випливає, що 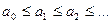 та
та
 .
.
Використовуючи ці співвідношення, отримуємо, що
 .
.
Аналогічно доводиться неперервність і за другим аргументом.
Достатність. Треба довести, що з неперервності за кожним аргументов випливає неперервність 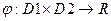 в цілому. Беремо довільний ланцюг і користуючись властивостями супремуму на декартовому добутку та неперервність за кожним аргументом, отримуємо наступні рівності:
в цілому. Беремо довільний ланцюг і користуючись властивостями супремуму на декартовому добутку та неперервність за кожним аргументом, отримуємо наступні рівності:
 .▄
.▄
Класи функцій на  -областях. Доведемо, що множина тотальних (всюди визначених) функцій F=
-областях. Доведемо, що множина тотальних (всюди визначених) функцій F=  на
на  -області є
-області є  -областю.
-областю.
Щоб відрізняти елементи та відношення на множинах F та D будемо вживати відповідні індекси, позначаючи частковий порядок на D як  , а на F – як
, а на F – як 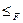 .
.
Спочатку визначимо частковий порядок 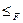 на F=
на F=  наступним чином (за точками).
наступним чином (за точками).
Нехай  . Тоді вважаємо, що
. Тоді вважаємо, що

 .
.
Для так введеного бінарного відношення виконуються всі аксіоми часткового порядку: рефлективність, транзитивність, антисиметричність.
Дійсно, оскільки 
 , то
, то 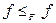 (рефлективність). Далі,
(рефлективність). Далі, 
 , тому
, тому  (транзитивність). Нарешті, справедливе співвідношення
(транзитивність). Нарешті, справедливе співвідношення 
 , з якого випливає
, з якого випливає  (антисиметричність).
(антисиметричність).
Тепер визначимо найменший елемент  . Тут вираз у квадратних дужках називається функціональним конструктором. Він задає значення функції на кожному її аргументі. Це означає, що
. Тут вираз у квадратних дужках називається функціональним конструктором. Він задає значення функції на кожному її аргументі. Це означає, що  (
(  ). Тому
). Тому  . За визначенням, це означає, що ^F
. За визначенням, це означає, що ^F 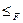 g.
g.
Далі треба продемонструвати повноту F. Нехай  – ланцюг в F. Треба довести, що
– ланцюг в F. Треба довести, що  F, тобто, що супремум функцій є функцією.
F, тобто, що супремум функцій є функцією.
Спочатку визначимо нову функцію  . Наведений функціональний конструктор задає значення функції на кожному її аргументі. Це означає, що
. Наведений функціональний конструктор задає значення функції на кожному її аргументі. Це означає, що 

 .
.
Доведемо, що  (
(  – найменша з мажорант ланцюга
– найменша з мажорант ланцюга  ).
).
1. Спочатку доведемо, що  – мажоранта множини функцій {
– мажоранта множини функцій {  }
} 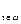 . Дійсно, за визначенням f
. Дійсно, за визначенням f 

 . Звідси випливає, що
. Звідси випливає, що 

 . Переставляючи універсальні квантори, отримуємо, що
. Переставляючи універсальні квантори, отримуємо, що 

 .
.
А це означає (за визначенням часткового порядку на F), що 
 . Тобто,
. Тобто,  – мажоранта множини функцій {
– мажоранта множини функцій {  }
} 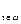 .
.
2. Доведемо тепер, що  – найменша мажоранта множини функцій {
– найменша мажоранта множини функцій {  }
} 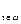 . Нехай
. Нехай  – довільна мажоранта цієї множини. Тоді
– довільна мажоранта цієї множини. Тоді

 Û
Û 
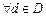
 Û
Û 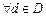

 Û
Û 

 Û
Û  .
.
Це означає, що доведена наступна лема.
Лема 5.6 Відображення  є супремумом множини функцій {
є супремумом множини функцій {  }
} 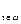 , тобто
, тобто  .
.
З доведених властивостей випливає, що множини неперервних функцій є  -областю. Отриманий результат можна посилити для випадку множини функцій
-областю. Отриманий результат можна посилити для випадку множини функцій  на
на  -областей D1 та D2.
-областей D1 та D2.
Лема 5.7 Множина функцій на  -областях є
-областях є  -областю.
-областю.
Неперервні функції на  -областях. Нехай F=
-областях. Нехай F=  – клас неперервних тотальних функцій на
– клас неперервних тотальних функцій на  -області D. Відношення часткового порядку на
-області D. Відношення часткового порядку на  є обмеженням часткового порядку на множині функцій
є обмеженням часткового порядку на множині функцій  , оскільки клас
, оскільки клас  є підкласом класу
є підкласом класу  . Залишилося довести, що
. Залишилося довести, що 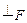 – неперервне відображення, і що супремум неперервних відображень є неперервним відображенням.
– неперервне відображення, і що супремум неперервних відображень є неперервним відображенням.
Доведемо неперервність відображення 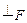 , тобто, що
, тобто, що 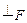 Î
Î  . Це означає, що треба довести рівність
. Це означає, що треба довести рівність  для довільного ланцюга
для довільного ланцюга  елементів з D. Дійсно,
елементів з D. Дійсно,  .
.
Лема 5.8 Якщо функції  ,
,  – неперервні, то функція
– неперервні, то функція  – також неперервна.
– також неперервна.
Доведення. За лемою 5.6, якщо  , то
, то  . Щоб довести, що
. Щоб довести, що  - неперервна, треба довести, що
- неперервна, треба довести, що  для довільного ланцюга
для довільного ланцюга  . Маємо, що (
. Маємо, що (  .
.
За лемою 5.2  , тому
, тому
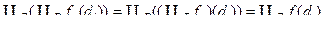 .▄
.▄
Це означає, що клас  є
є  -областю. Отриманий результат можна посилити для випадку множини неперервних функцій
-областю. Отриманий результат можна посилити для випадку множини неперервних функцій 
 -областей D1 та D2 . Це дозволяє сформулювати наступний результат.
-областей D1 та D2 . Це дозволяє сформулювати наступний результат.
Лема 5. 9 Множина неперервних функцій на  -областях є
-областях є  -областю.
-областю.
5.6 Властивості оператора найменшої нерухомої точки
Операцію взяття нерухомої точки можна трактувати як оператор  , де
, де  – множина неперервних відображень. Доведемо, що оператор lfp – неперервний. Але спочатку покажемо, що він – монотонний.
– множина неперервних відображень. Доведемо, що оператор lfp – неперервний. Але спочатку покажемо, що він – монотонний.
Лема 5. 10 Відображення  – монотонне відображення, тобто
– монотонне відображення, тобто  для
для 
 .
.
Доведення. Нехай  . Розглянемо наступні співвідношення:
. Розглянемо наступні співвідношення:

| ££D | 
| |
g(  ) )
| ££D | h(  ) )
| (Умова 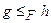 ) )
|
g(g(  )) ))
| ££D | g(h(  ))£D h(h( ))£D h(h(  )) ))
| (Монотонність g та умова 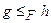 ) )
|
| … | … | … | … |
g(k)(  ) )
| ££D | …£D g(k-m)(h(m) (  ))…£D h(k) ( ))…£D h(k) (  ) )
| (Монотонність g та умова 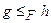 ) )
|
| … | … | … | … |

| ££D | 
|
Оскільки lfp(g)=  та lfp(h)=
та lfp(h)=  , то
, то 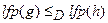 .▄
.▄
Теорема 5. 3 (неперервність lfp) Якщо  –
–  -область, то відображення
-область, то відображення 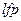 - неперервне, тобто
- неперервне, тобто  .
.
Доведення. Неперервність 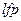 означає, що для довільного ланцюга
означає, що для довільного ланцюга  має виконуватись співвідношення
має виконуватись співвідношення
 .
.
Спочатку доведемо, що  . Оскільки
. Оскільки  , то за лемою 5.10
, то за лемою 5.10 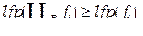 для довільного
для довільного  , а отже
, а отже  .
.
Тепер доведемо, що  . Для цього доведемо, що
. Для цього доведемо, що  - нерухома точка для
- нерухома точка для  ( тобто,
( тобто,  ). Дійсно
). Дійсно
 .Позначимо
.Позначимо  ,
,  . Неважко довести, що засновки леми 5.2 виконуються, тому
. Неважко довести, що засновки леми 5.2 виконуються, тому
 =
= 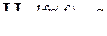 .
.
Оскільки  - найменша нерухома точка, то вона менша за будь-яку нерухому точку для
- найменша нерухома точка, то вона менша за будь-яку нерухому точку для 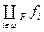 . Тому
. Тому 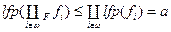 .
.
Отже ми довели, що  .▄
.▄
Таким чином, досліджено основні властивості оператора найменшої нерухомої точки, який може вважатися одним із уточнень рекурсії.
5.7 Застосування теорії ННТ
Найважливішими способами визначення нескінченних об’єктів (множин, послідовностей, функцій і таке інше), є рекурентні, індуктивні та рекурсивні способи. Оскільки перші два способи є частковими випадками рекурсії, то звідси випливає важливість теорії ННТ, як одного із способів уточнення рекурсіх, в різних застосуваннях. Тут ми розглянемо застосування ННТ для уточнення синтаксису та семантики мов програмування.
5.7.1 Уточнення синтаксису мов програмування
Синтаксис мов програмування переважно задається за допомогою БНФ, граматик та інших подібних формалізмів. Сама структура правил БНФ говорить про можливість застосування теорії ННТ для уточнення формальних мов, що задаються БНФ.
В попередньому розділі було розглянуто приклад подання породжуючої граматики як системи рівнянь.
Так, правила  задають мову, яка є розв’язком рівняння
задають мову, яка є розв’язком рівняння  . Але для того, щоб стверджувати існування розв’язку, необхідно дослідити область, на якій задаються такі рівняння.
. Але для того, щоб стверджувати існування розв’язку, необхідно дослідити область, на якій задаються такі рівняння.
Розглянемо алгебру, на якій задано наведене рівняння (відображення  ):
):
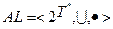 , де
, де
 – множина слів, <
– множина слів, <  > – операції об’єднання та конкатенації.
> – операції об’єднання та конкатенації.
Достатніми умовами існування розв’язків рекурсивних рівнях в алеграх наведеного типу є умови для множини  бути w-областю, та для операцій об’єднання та конкатенації буди неперервними. Доведемо виконання цих умов.
бути w-областю, та для операцій об’єднання та конкатенації буди неперервними. Доведемо виконання цих умов.
Лема 5.11. Множина  – w-область
– w-область
Доведення. Щоб множина була w-областю треба визначити на ній
частковий порядок та показати його повноту та найменший елемент.
Для множини  частковим порядком буде включення, порожня множина буде найменшим елементом, а об’єднання множин буде супремумом, тобто є така відповідність:
частковим порядком буде включення, порожня множина буде найменшим елементом, а об’єднання множин буде супремумом, тобто є така відповідність:
1) 

2) 



3) 
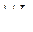
Очевидно, що всі необхідні умови w-області виконуються для так введеного часткового порядку.▄
Лема 5.12. Операції об’єднання та конкатенації – w-неперервні.
Доведення. Розглянемо операцію об’єднання  . Згідно леми 5.5 досить довести неперервність об’єднання за кожним аргументом. Не обмежуючи загальності, доведемо неперервність за першим аргументом.
. Згідно леми 5.5 досить довести неперервність об’єднання за кожним аргументом. Не обмежуючи загальності, доведемо неперервність за першим аргументом.
Нехай  – ланцюг з множини
– ланцюг з множини  ,
,  Î
Î  ,
,  . За визначенням,
. За визначенням,  . Щоб довести неперервність, треба показати, що
. Щоб довести неперервність, треба показати, що  . Дійсно, для довівільного елемента x маємо
. Дійсно, для довівільного елемента x маємо



Отже  – неперервна операція.
– неперервна операція.
Розглянемо тепер операцію  . За визначенням,
. За визначенням,
 .
.
Доведемо, що  . Маємо, що
. Маємо, що



Отже операція  також неперервна.▄
також неперервна.▄
Таким чином, множина формальних мов є w-областю, а операції слабкої алгебри формальних мов – неперервними. Похідні операції також будуть неперервними. Тому рекурсивні визначення (рівняння) над цією алгеброю завжди мають найменший розв’язок. Цей розв’язок, за теоремою КТК, можна знайти методом послідовних наближень.
Доведемо, що якщо за КВ-граматикою побудувати відповідну систему рекурсивних визначень, то розв’язок цієї системи співпаде з мовою, породженою граматикою.
Отже, нехай G = (N, Т, Р, S) – КВ-граматика, aÎ(NÈT)*. Задамо відображення s:(NÈT)®(NÈ2T), вважаючи, що s(A)=A, AÎN, та s(a)={a}, aÎT. Це відображення розповсюджуємо на послідовності символів з алфавіту (NÈT), вважаючи, що s(x 1 x 2 … xn)=s(x 1)s(x 2)… s(xn). Тепер маємо, що s:(NÈT)*®(NÈ2T)*. Сукупність всіх правил A ® a 1,A ® a 2, …, A ® a k з граматики G з одним і тим же нетерміналом у лівій частині замінюємо на рекурсивне визначення A = s(a 1)Ès(a 2)È…Ès(a k). Такі визначення будуємо для всіх нетерміналів. Отриману систему рекурсивних визначень над слабкою алгеброю формальних мов позначимо E(G). Відображення, що задається правими частинами цієї системи позначимо jG, його складову за нетерміналом A позначимо jA, а найменшу нерухому точку цього відображення за змінною (нетерміналом) S позначимо lfpS(jG).
Приклад 5.1. Для граматики G = ({S, A, B, C, D}, {a, b, c), P, S), де P складається з наступних правил:
S®AB | CD | e
A®e| aA
B®e| bB c
C®e| a C b
D®e| c D
отримуємо наступну систему рекурсивних визначень:
S=AB È CD È {e}
A={e} È {a}A
B={e} È {b}B{c}
C={e} È{a}C{b}
D={e} È {c}D
Доведемо тепер, що мова, породжена КВ-граматикою, співпадає з найменшим розв’язком системи рекурсивних визначень (рівнянь), побудованих за цією граматикою.
Теорема 5.4 Для КВ-граматики G = (N, Т, Р, S)
L(G)= lfpS(jG).
Доведення. Нехай L(k)A(G) – множина термінальних ланцюжків породжених з нетермінала A деревами виводу глибини не більше k. Індукцією за k доводимо, що
L(k)A(G)=j(k)A(^).
Дійсно, для виводів довжини 0 маємо, що L(0)A(G)=Æ та j(0)A(^)=^=Æ.
Припускаючи, що індуктивна гіпотеза вірна для k, доведемо її справедливість для k +1. Дійсно, мова L(k +1)A(G) складається з термінальних ланцюжків t, які виводяться з A деревами виводу глибини не більше k +1. Такі дерева породжуються деяким правилом A ® x 1 x 2 … xnÎP, а виводи з нетермінальних символів з x 1, x 2, …, xn мають глибину не більшу k. Термінальні ланцюжки, що породжуються з таких нетерміналів x входять у мову j(k)x(^). З побудови j(k +1)A(^) випливає, що ланцюжок t буде належати цій мові. Також є вірним і зворотнє: якщо tÎj(k +1)A(^), то tÎL(k +1)A(G). Індуктивна гіпотеза доведена. Звідси випливає справедливість теореми.▄
Таким чином, для подання формальних мов можна використовувати формалізм рекурсивних визначень та теорію ННТ. Правда, цей формалізм є більш потужним, якщо допускається використання нескінченних мов у визначеннях. Разом з тим, неважко довести, що для слабко рекурсивних визначень (із скінченними мовами у визначеннях), найменшими розв’язками будуть лише КВ-мови.
Вибір формалізму подання синтаксису залежить від способу його використання (від прагматики).
Тепер розглянемо використання теорії ННТ для подання семантики мов програмування.
5.7.2 Семантика мов програмування
В першому розділі посібника семантика програм мови SIPL задавалась функціями програмної алгебри
A_Prog =<FNA, FNB, FNAB, FA, FB, FS; Sn, ASx, ·, IF, WH, xÞ, id >.
Програми мови SIPL не є рекурсивними, але легко зробити таке її розширення, яке буде мати рекурсивні функції та процедури (це буде зроблено пізніше). Тому здається вірогідним, що класи часткових функцій алгебри A_Prog (класи FA, FB, FS) є w-областями, а композиції, задані на цих класах – неперервними. Це дійсно так.
Доведемо більш загальний результат. Нехай D, R – деякі множини даних, а  – клас часткових функцій, заданих на цих множинах. Введемо на F відношення часткового порядку £, вважаючи, що для функцій f,g ÎF
– клас часткових функцій, заданих на цих множинах. Введемо на F відношення часткового порядку £, вважаючи, що для функцій f,g ÎF
f£g  .
.
Якщо використовувати графіки функцій, то можна записати, що
f£g  .
.
Очевидно, що так введене бінарне відношення є дійсно відношенням частково порядку. Найменшим елементом буде всюди невизначена функція, для якої залишемо позначення ^.
Супремумом ланцюга функцій  буде функція f =
буде функція f =  , графік якої є об’єднання графіків функцій ланцюга, тобто
, графік якої є об’єднання графіків функцій ланцюга, тобто  . Неважко переконатись, це об’єднання є функціональним бінарним відношенням. Дійсно, нехай
. Неважко переконатись, це об’єднання є функціональним бінарним відношенням. Дійсно, нехай 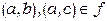 . Це означає, що
. Це означає, що
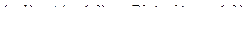 ,
,
 .
.
Якщо  , аналогічно розглядається випадок
, аналогічно розглядається випадок  .
.
Тобто f є дійсно функцією. Це говорить про повноту F.
Таким чином, доведено наступне твердження.
Лема 5.13. Множина  часткових функцій із D в R є w-область.
часткових функцій із D в R є w-область.
Зауважимо відмінність цієї леми від лем 5.7 та 5.9, які говорять про класи тотальних функцій, частковий порядок на яких індукується частковим порядком на їх областях визначення та значень. В лемі 5.3 говориться про клас часткових функцій, визначенних на довільних множинах, які не обов’язково є w-областями. В зв’язку з цим класи n-арних тотальних функцій FNA, FNB, FNAB не підпадають під дію леми 5.13.
Застосовуючи лему 5.13 до наступних класів (основ) часткових функцій алгебри A_Prog: FA, FB, FS, отримуємо, що ці основи є w-областями.
Доведемо тепер, що композиції Sn, ASx, ·, IF, WH, xÞ, id алгебри A_Prog є неперервними.
Це очевидно для нуль-арних композицій (функцій) xÞ і id, які не мають функцій-аргументів.
Лема 5.14. Композиція суперпозиції Sn номінативних функцій в n-арну функцію неперервна за номінативними функціями-аргументами.
Доведення. Нехай f – n-арна функція, g1,…,gn – номінативні функції типу FA,  – ланцюг функцій з FA, stÎState. Значення обчислюється за наступною формулою:
– ланцюг функцій з FA, stÎState. Значення обчислюється за наступною формулою:
Sn(f, g1,…,gn ))(st)=f(g1(st),…,gn(st)).
Доведемо неперервність суперпозиції за першим аргументом типу FA, тобто доведемо, шо Sn(f,  ,…,gn )=
,…,gn )= 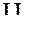 Sn(f,
Sn(f,  ,…,gn ).
,…,gn ).
Нехай Sn(f,  ,…,gn ))(st)¯=r. Отримуємо наступну послідовність еквівалентних перетворень:
,…,gn ))(st)¯=r. Отримуємо наступну послідовність еквівалентних перетворень:
Sn(f,  ,…,gn ))(st)¯=rÛf(
,…,gn ))(st)¯=rÛf(  (st),…,gn(st))¯=r Û
(st),…,gn(st))¯=r Û
Û$k(f(fk(st),…,gn(st))¯=rÛ 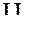 Sn(f,
Sn(f,  ,…,gn )(st)¯=r.
,…,gn )(st)¯=r.
Наведені перетворення спираються на той факт, що
 (st)¯=r ¢ Û $k(fk(st)(st)¯=r ¢.▄
(st)¯=r ¢ Û $k(fk(st)(st)¯=r ¢.▄
Аналогічним чином доводиться наступне твердження.
Лема 5.15. Композиція присвоєння ASx – неперервна.
Доведемо неперервність послідовного виконання.
Лема 5.16. Композиція послідовного виконання  – неперервна.
– неперервна.
Доведення. Щоб довести неперервність композиції  , нам потрібно довести неперервність
, нам потрібно довести неперервність  за кожним аргументом. Доведемо лише неперервність за першим аргументом, тобто, що
за кожним аргументом. Доведемо лише неперервність за першим аргументом, тобто, що  . Маємо, що
. Маємо, що
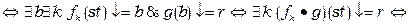
 .▄
.▄
Лема 5.17. Композіція  – неперервна.
– неперервна.
Доведення. Щоб довести неперервність композиції  , нам потрібно довести неперервність
, нам потрібно довести неперервність  за кожним аргументом. Розглянемо лише доведення неперервності за одним аргументом, так як за іншими вона доводиться аналогічно. Нагадаємо, що
за кожним аргументом. Розглянемо лише доведення неперервності за одним аргументом, так як за іншими вона доводиться аналогічно. Нагадаємо, що

Розглянемо перший випадок:  . Тоді
. Тоді

 .▄
.▄
Для доведення неперервності композицій ітерації (циклу) спочатку покажемо, що ітерація функцій є найменшою нерухомою точкою певного рекурсивного визначення.
Теорема 5.5. Для композиції циклу виконується наступне співвідношення:

Доведення.
Раніше (лема 1.2) було доведено, що  є нерухомою точкою рівняння X=IF(fb, f s · X, id), звідки випливає, що
є нерухомою точкою рівняння X=IF(fb, f s · X, id), звідки випливає, що  . Тому залишилось довести, що
. Тому залишилось довести, що  .
.
Попередньо нагадаємо початкове визначення композиції циклу  (розділ 1):
(розділ 1):
WH(fb,f s)(st)=stn, де st0=st, st1=f s(st0), st2=f s(st1), …, stn=f s(stn-1), причому fb(st0)=true, fb(st1)=true,…, fb(stn-1)=true, fb(stn)=false.
Тепер позначимо  . Тоді
. Тоді  . Також будемо позначати
. Також будемо позначати  той факт, що обчислення
той факт, що обчислення  на даному st завершилось з результатом
на даному st завершилось з результатом  при числі ітерацій, не більше ніж k, тобто NumIt WH((p, f), st))£k.
при числі ітерацій, не більше ніж k, тобто NumIt WH((p, f), st))£k.
Доведемо індукцією за k), що з умови  , випливає (
, випливає (  )(st)¯=stk . (Усі твердження такого типу вважаються універсально квантифікованими, в даному випадку за st та stk.)
)(st)¯=stk . (Усі твердження такого типу вважаються універсально квантифікованими, в даному випадку за st та stk.)
База індукції (k = 0). З умови  , випливає, що st 0=st, та
, випливає, що st 0=st, та  . Оскільки
. Оскільки  , то при вказаних умовах будемо мати, що (
, то при вказаних умовах будемо мати, що (  )(st)¯=st.
)(st)¯=st.
Індуктивний крок. З припущення, що індуктивна гіпотеза справедлива для k, доведемо її справедливість для k+1.
Дійсно, нехай  . Тоді з леми 1.2 випливає, що
. Тоді з леми 1.2 випливає, що 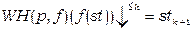 та що
та що  . За індуктивною гіпотезою маємо, що (
. За індуктивною гіпотезою маємо, що (  )(f(st))¯=stk+1. Звідси випливає, що (
)(f(st))¯=stk+1. Звідси випливає, що (  )(st)¯=stk+1, бо
)(st)¯=stk+1, бо  =
=  і при обчисленні маємо, що
і при обчисленні маємо, що
(  )(st) = (
)(st) = (  )(st) =
)(st) =
=  (st) = (
(st) = (  )(f(st))= stk+1.▄
)(f(st))= stk+1.▄
Лема 5.18. Композиція  - неперервна.
- неперервна.
Доведення. Скориставшись доведеними результатами щодо циклу та неперервності композицій послідовного виконання та умовного оператора, отримуємо, що

 .
.
Аналогічним чином доводиться неперервність і за першим аргументом.▄
Доведені леми про неперервність композицій алгебри A_Prog дозволяють стверджувати, що похідні композиції, які можна визначити в цій алгебрі, також будуть неперервними. (Питання про точне визначення похідних композицій буде розглянуто пізніше.)
Факт неперервності композицій алгебри A_Prog не є випадковим. Має місце наступне твердження.
Твердження 5.1. Програмні композиції (які обчислюються за скінченну кількість кроків) – неперервні.
Доведення ґрунтується на тому факті, що для обчислення значень функцій, побудованих за допомогою програмних композицій, використовується лише скінченна частина (скінченний графік) функцій-аргументів. Деталі доведення тут не наводимо.
Таким чином, найважливіший висновок з теорії ННТ полягає в тому, що семантика мов програмування задається класами функцій, які є  -областями, а композиції таких функцій є неперервними операторами. Це дозволяє обґрунтувати коректність використання різних рекурсивних методів для визначення засобів конструювання програм, спираючись на теореми, доведені в теорії ННТ.
-областями, а композиції таких функцій є неперервними операторами. Це дозволяє обґрунтувати коректність використання різних рекурсивних методів для визначення засобів конструювання програм, спираючись на теореми, доведені в теорії ННТ.
Проілюструємо введення рекурсивних визначень функцій для розширення мови SIPL.
5.7.3 Рекурсивні розширення мови SIPL
Спочатку розглянемо приклади рекурсивних визначень функцій.
Приклад 5.1 Функцію n ! часто задають наступним рекурсивним визначенням:
f(n) = if n > 1 then n*f(n-1) else 1
Основна складність таких визначень полягає у відсутності їх стандартного семантичного уточнення. Одне з можливих уточнень має операційний характер, а саме, вважається, що при обчисленні значення, наприклад, f(5), обчислюється права частина рекурсивного визначення (відбувається розгортка визначення при заміні n на 5). Це обчислення призведе до необхідності обчислення f(4), що у свою чергу потребує обчислення f(3), і т.д. І тільки обчислення f(1) дасть результат 1, що дозволить обчислити f(2), f(3), f(4), f(5).
Аналіз цієї процедури обчислень показує, що обчислення фактично пов’язані з перетворенням виразів, їх «переписуванням», «розгорткою» для нових аргументів функцій (англійською – rewriting). Але порядок застосувань переписуючих правил також чітко не визначений. Тому виникають різні можливості розгортки рекурсивної функції, коли замінюється праве входження функції, чи ліве, чи внутрішнє, чи зовнішнє. Цей порядок має визначатись семантикою визначень, тому ми знову повертаємось до питання про семантику рекурсивних визначень.
Тут будемо застосовувати композиційно-номінативну семантику виразів. Це означає, що права частина буде тлумачитисть як номінативна функція, побудована з простих функцій за допомогою композицій.
Перше питання, що виникає, є наступним: яка номінативна функція відповідає виразу if n > 1 then n*f(n-1) else 1? Попереднє тлумачення, коли ми вживали виклики функції виду f(5), f(4) і т.д., говорить про те, що f є унарною функцією типу Int ® Int. Тут фактично n є позначенням числа. Таке тлумачення для програмування не є вдалим, тому що для програмування є природним вживання функцій над іменованими значеннями (детальніше це буде обговорюватись у подальших розділах). Тому будемо вважати, що виразу if n > 1 then n*f(n-1) else 1 відповідає функція, задана на станах змінних, причому n є однією із змінних. Але оскільки ми вже «зарезервували» n для позначення довільного числа, будемо змінну позначати прописною (великою) літерою N. Це означає, що нам краще переписати визначення саме у такій формі:
f(N) = if N > 1 then N*f(N-1) else 1
Отже, права частина визначення задає функцію, що обчислюється на даних виду [Nan] та на їх розширеннях.
При побудові семантичного терму цього виразу виникає питання про тлумачення виразу f(N-1). Зрозуміло, що це буде суперпозиція функції S2(sub, N Þ,  ), яка задається виразом N-1, в функцію f. Але функція f є номінативною, а не є n-арною функцію. Тому треба визначити суперпозицію у номінативні функції. Такіх суперпозицій може буде декілька, зокрема глобальна та локальні суперпозиції. У глобальна суперпозиції аргумент функції f формується повністю (як цілісність). У локальній суперпозиції формуються лише одна частина аргументу f, а інша буреться із вхідного даного. Ці міркування і ведуть до наступних визначень суперпозицій.
), яка задається виразом N-1, в функцію f. Але функція f є номінативною, а не є n-арною функцію. Тому треба визначити суперпозицію у номінативні функції. Такіх суперпозицій може буде декілька, зокрема глобальна та локальні суперпозиції. У глобальна суперпозиції аргумент функції f формується повністю (як цілісність). У локальній суперпозиції формуються лише одна частина аргументу f, а інша буреться із вхідного даного. Ці міркування і ведуть до наступних визначень суперпозицій.
Глобальною суперпозицією функцій g1,g2,…,gn в номінативну функцію f називається функція, яка задається формулою
S(v1,v2,..vn)(f,g1,g2,…,gn)(st)=f([v1ag1(st),v2ag2(st),…, vnagn(st)])
Докальною суперпозицією функцій g1,g2,…,gn в номінативну функцію f називається функція, яка задається формулою
S[v1,v2,..vn](f,g1,g2,…,gn)(st)=f(stÑ[v1ag1(st),v2ag2(st),…, vnagn(st)])
Зауважимо, що традиційна суперпозиція в n-арну функцію може розглядатися як частковий випадок глобальної суперпозиції при тлумаченні 1, …, n як імен аргументів функції f. Тому
Sn(f,g1,g2,…,gn)=S(1,2,…,n) (f,g1,g2,…,gn)
Повернемось тепер до побудови семантичного терму виразу
if N > 1 then N*f(N-1) else 1
Хоча можна обрати глобальну суперпозицію, візьмемо локальну суперпозицію як більш адекватну задачам програмування. Отримуємо семантичний терм
j(f)= IF(S2(gr, N Þ,  ), S2(mult, N Þ, S [N](f, S2(sub, N Þ,
), S2(mult, N Þ, S [N](f, S2(sub, N Þ,  )),
)),  )
)
Неважко довести, що введені композиції суперпозиції є неперервними, тому теорема КТК є застосовною. Це означає, що існує ННТ j(f), яку можна отримати методом послідовних наближень. Обчислимо декілька таких наближень.
Початковим наближенням є всюди невизначена функція
f0 = ^.
Наступне наближення отримуємо підстановкою попереднього наближення в оператор j.
f1 = j(f0) =j(^) = IF(S2(gr, N Þ,  ), S2(mult, N Þ, S [N](^, S2(sub, N Þ,
), S2(mult, N Þ, S [N](^, S2(sub, N Þ,  )),
)),  ) = =IF(S2(gr, N Þ,
) = =IF(S2(gr, N Þ,  ), S2(mult, N Þ, ^),
), S2(mult, N Þ, ^),  )=IF(S2(gr, N Þ,
)=IF(S2(gr, N Þ,  ), ^,
), ^,  ).
).
Наведені рівності мають місце тому, що суперпозиція всюди невизначеної функції, або суперпозиція у всюди невизначену функцію, має своїм результатом всюди невизначену функцію, тобто S [N](^, S2(sub, N Þ,  ))=^ та S2(mult, N Þ, ^)=^. Тому суперпозицію часто називають строгою операцією, бо вона зберігає всюди невизначену функцію.
))=^ та S2(mult, N Þ, ^)=^. Тому суперпозицію часто називають строгою операцією, бо вона зберігає всюди невизначену функцію.
Наближення f1 можна записати за допомогою її графіка наступним чином
f1([Nan])= IF(S2(gr, N Þ,  ), ^ ,
), ^ ,  ) ([Nan])=
) ([Nan])= 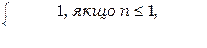
Обчислимо друге наближення.
f2 = j(f1) = IF(S2(gr, N Þ,  ), S2(mult, N Þ, S [N](f1, S2(sub, N Þ,
), S2(mult, N Þ, S [N](f1, S2(sub, N Þ,  )),
)),  )=
)=
=IF(S2(gr, N Þ,  ), S2(mult, N Þ, S [N](IF(S2(gr, N Þ,
), S2(mult, N Þ, S [N](IF(S2(gr, N Þ,  ), ^,
), ^,  ),
),
S2(sub, N Þ,  )),
)),  ).
).
Аналіз отриманого виразу говорить про те, що з’явилось нове значення при  . Це значення можна обчислити на f2([Na2]) так, як це ми робили раніше.
. Це значення можна обчислити на f2([Na2]) так, як це ми робили раніше.
Це дає можливість записати наближення f2 за допомогою його графіка наступним чином
f2([Nan])= 
Наведені наближення дозволяють сформулювати гіпотезу, що
f k([Nan])= 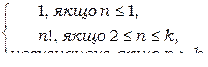
Цю гіпотезу можна довести індукцією за k.
Для k =1 гіпотеза справедлива.
Доведемо її справедливість для k +1, виходячи з того, що вона справедлива для k. Маємо, що
fk +1 = j(f k) = IF(S2(gr, N Þ,  ), S2(mult, N Þ, S [N](f k, S2(sub, N Þ,
), S2(mult, N Þ, S [N](f k, S2(sub, N Þ,  )),
)),  )
)
В силу монотонності j «старі» значення функції f k не зміняться, але можуть появитися нові значення. Це можливо лише для даного [Nak +1]. Дійсно, обчислення fk +1 дає
fk +1([Nak +1])=j(f k) =
= IF(S2(gr, N Þ,  ), S2(mult, N Þ, S [N](f k, S2(sub, N Þ,
), S2(mult, N Þ, S [N](f k, S2(sub, N Þ,  )),
)),  )([Nak +1])=
)([Nak +1])=
=S2(mult, N Þ, S [N](f k, S2(sub, N Þ,  ))([Nak +1])=
))([Nak +1])=
=mult (N Þ([Nak +1]), S [N](f k, S2(sub, N Þ,  ))([Nak +1]))=
))([Nak +1]))=
=mult (k +1, f k([Nak +1] Ñ[NaS2(sub, N Þ,  )([Nak +1])])=
)([Nak +1])])=
=mult (k +1, f k([Nak +1] Ñ[Nasub(N Þ([Nak +1]),  ([Nak +1]))]))=
([Nak +1]))]))=
=mult (k +1, f k([Nak +1] Ñ[Nasub(k +1,1)]))=
=mult (k +1, f k([Nak +1] Ñ[Nak]))=mult (k +1, f k([Nak +1] Ñ[Nak]))=
= mult (k +1, f k([Nak]))=mult (k +1, k!)=(k+1)!
Для даних, більших за k +1, значення fk +1 буде невизначеним.
Границя послідовності f 0, f 1, f 2,… дає функцію f w =  , яка є найменшою нерухомою точкою оператора j, тобто f w =
, яка є найменшою нерухомою точкою оператора j, тобто f w =  =lfp f j . Функція f w на даному [Nan] приймає значення n! (для n >0). Таким чином, теорія найменшої нерухомої точки дає обґрунтування рекурсивним визначенням наведеного типу.
=lfp f j . Функція f w на даному [Nan] приймає значення n! (для n >0). Таким чином, теорія найменшої нерухомої точки дає обґрунтування рекурсивним визначенням наведеного типу.
Приклад 5.2 Знайдемо ННТ рекурсивного визначення найбільшого спільного дільника чисел n та m. Традиційне рекурсивне визначення має такий вигляд.
f(n, m) = if n > m then f(n-m, m) else if n < m then f(n, m-n) else m
Таке визначення зазвичай трактують як визначення певної бінарної функції. Хоча можна побудувати теорію ННТ і для n-арних функцій (зробіть це самостійно), ми перейдемо до класу номінативних функцій (над даними з іменами M та N). Тоді наше визначення перепишемо у наступному вигляді:
f(N, M) = if N > M then f(N-M, M) else if N < M then f(N, M-N) else M
Побудуємо семантичний терм правої частини цього визначення.
j(f)= IF(S2(gr, NÞ, MÞ), S [N,M](f, S2(sub, N Þ, MÞ), MÞ), IF(S2(less, NÞ, MÞ), S [N,M](f, NÞ, S2(sub, M Þ, NÞ), MÞ))
Зауважимо, що можна взяти суперпозицію за одним іменем, а саме
j¢(f)= IF(S2(gr, NÞ, MÞ), S [N](f, S2(sub, N Þ, MÞ)), IF(S2(less, NÞ, MÞ), S [M](f, S2(sub, M Þ, NÞ), MÞ))
Також можна брати глобальну суперпозицію:
j¢¢(f)= IF(S2(gr, NÞ, MÞ), S (N,M)(f, S2(sub, N Þ, MÞ), MÞ), IF(S2(less, NÞ, MÞ), S (N,M)(f, NÞ, S2(sub, M Þ, NÞ), MÞ))
Для спрощення перетворень, візьмемо варіант для j¢.
Початковим наближенням є всюди невизначена функція
f0 = ^.
Наступне наближення отримуємо підстановкою попереднього наближення в оператор j¢.
f1 = j¢(f0) =j¢(^)= IF(S2(gr, NÞ, MÞ), S [N](^, S2(sub, N Þ, MÞ)), IF(S2(less, NÞ, MÞ), S [M](^, S2(sub, M Þ, NÞ), MÞ))=IF(S2(gr, NÞ, MÞ), ^, IF(S2(less, NÞ, MÞ), ^, MÞ))
Графік задається наступною формулою:
f1([Nan,Mam])=
=IF(S2(gr, NÞ, MÞ), ^, IF(S2(less, NÞ, MÞ), ^, MÞ))([Nan,Mam])=
= 
Запишемо графік f1 трошки іншим чином, фактично вводячи r як найбільший спільний дільник:
f1([Nan,Mam])=
= 
Обчислимо друге наближення.
f2 = j¢(f1) = IF(S2(gr, NÞ, MÞ), S [N](f1, S2(sub, N Þ, MÞ)), IF(S2(less, NÞ, MÞ), S [M](f1, S2(sub, M Þ, NÞ), MÞ)).
Його графік задається наступною формулою:
f2([Nan,Mam])=
=IF(S2(gr, NÞ, MÞ), S [N](f1, S2(sub, N Þ, MÞ)), IF(S2(less, NÞ, MÞ), S [M](f1, S2(sub, M Þ, NÞ), MÞ))([Nan,Mam])=
= 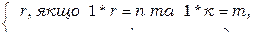

Побудувати самостійно наступні наближення, та довести, що їх границя задає функції знаходження найбільшого спільного дільника.
Побудуємо тепер розширення мови SIPL, які позволяють використовувати рекурсивні визначення такого типу, як у розглянутих прикладах.
Синтаксис розширення – БНФ – подамо у наступній таблиці.
Таблиця 5.1
| Ліва частина правила – метазмінна | Права частина правила | Ім’я правила |
| <програма> ::= | …| program <списокоб’явленьфункцій> begin <оператор> end | NP1 NP2 |
| <вираз> ::= | …| if <умова> then <вираз> else <вираз> | <виклик функції> | NA1–NA7 NA8 NA9 |
| <списокоб’явленьфункцій>::= | e | <об’явленняфункції> | <об’явленняфункції> ; <списокоб’явленьфункцій> | LDF1 LDF2 LDF3 |
| <об’явленняфункції>::= | func <ім’я функції>=<вираз> | func <ім’я функції>(<списокформальних параметрів>)= <вираз> | DF1 DF2 |
| <ім’я функції> ::= | <змінна> | NF |
| <списокформальних параметрів>::= | <змінна> | <змінна> , <списокформальних параметрів> | LFP1 LFP2 |
| <виклик функції> ::= | <ім’я функції> | <ім’я функції> (<списокфактичних параметрів>) | CF1 CF2 |
| <списокфактичних параметрів>::= | <вираз> | <вираз> , <списокфактичних параметрів> | LAP1 LAP2 |
В більш математичному вигляді ці розширення можна задати наступним чином:
Таблиця 5.2
| Ліва частина правила – метазмінна | Права частина правила | Ім’я правила |
| P::= | …| program dec1;…;decn begin S end | P1 P 2 |
| a::= | …| if b then a1 else a2 | fc | A1– A7 A8 A9 |
| dec ::= | func fn=a | func fn(x1,…,xn)= a | DF1 DF2 |
| fn ::= | x | NF |
| fc ::= | fn | fn(a1,…,an) | CF1 CF2 |
Семантичні правила повинні врахувати наявність рекурсивних визначень. Тому ці правила ускладнюються, бо з’являється аргумент E, який називаємо середовищем. Неформально, середовище можна трактувати як відображення, яке імені функції fn, заданого рекурсивним визначенням func fn(x 1 ,…, xn)= a, співставляє формальні параметри (x 1 ,…, xn) та семантику виразу a. Далі ця інформація використовується для подання семантики викликів функцій. Деталі тут розписувати не будемо.
Висновки
В цьому розділі було розглянуто основи теорії рекурсивних визначень. Основним методом знаходження об’єкту, що задається рекурсивним визначенням, є метод послідовних наближень. Щоб цей метод був коректним, клас об’єктів має бути w-областю (повною частково впорядкованою множиною з найменшим елементом), а операції над об’єктами – неперервними. В цьому випадку теорема Кнастера–Тарського–Кліні гарантує існування найменшого розв’язку (найменшої нерухомої точки неперервного оператора), який знаходиться методом послідовних наближень. Множина нерухомих точок також утворює w-область, а відображення, яке неперервному оператору співставляє найменшу нерухому точку, також є неперервним. Традиційні методи побудови більш складних областей дозволяють будувати нові w-області з більш простих w-областей. Застосування теорії найменшої нерухомої точки є надзвичайно широким. Зокрема, ця теорії може бути застосована для визначення синтаксису формальних мов за допомогою БНФ та подібних методів. Семантика рекурсивних програм також може бути визначена за допомогою цієї теорії. Важливо відзначити, що семантичні області є w-областями, а засоби конструювання програм – композиції – є неперервними. Ці властивості гарантують наявність адекватного тлумачення рекурсивних програм.
Контрольні питання.
1. Що таке рекурсивне визначення (рекурсивне визначення)?
2. Які парадокси пов’язані з рекурсивними визначеннями?
3. Який метод застосовують для розв’язку рекурсивних рівнянь? Які поняття пов’язані з цим методом?
4. Що таке перший граничний (перший нескінченний) ординал?
5. Що таке  -область?
-область?
6. Дайте визначення неперервного відображення.
7. Сформулюйте теорему Кнастера-Тарського-Кліні.
8. Яку структуру має множина нерухомих точок неперервного оператора?
9. Визначте методи конструювання похідних областей.
10. Сформулюйте властивості оператора найменшої нерухомої точки.
11. Вкажіть на застосування теорії ННТ для подання синтаксису мов програмування.
12. Вкажіть на застосування теорії ННТ для подання семантики мов програмування.
13. Як визначаються рекурсивні розширення мови SIPL.
14. Наведіть приклади рекурсивних визначень у розширеннях мови SIPL.
Вправи.
1. Розбудуйте теорію ННТ для класу n-функцій.
2. Для задач з розділу 1 побудуйте рекурсивні визначення.
3. Доведіть коректність побудованих рекурсивних визначень.
[1] http://www.slovnyk.net/
[2] http://www.m-w.com/cgi-bin/dictionary.
[3] Серед різних значень слова 'програма' виділимо лише ті, які близкі до предмету нашого розгляду.
[4] The Free On-line Dictionary of Computing – http://work.ucsd.edu:5141/cgi-bin/http_webster
Дата добавления: 2019-02-13; просмотров: 299; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
