Малюнок 2.7. Програма як діалектичне заперечення проблеми 6 страница

2. S 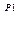 aBSc  aBc abc.

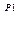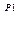3. S  aBSc  aBaBScc  aBaBcc 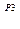 aaBBcc  aaBbcc  aabBcc  aabbcc.

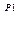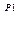4. S aBSc  aBaBScc  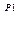aBaBaBSccc  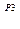aBaaBBSccc  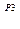aaBaBBSccc  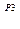aaaBBBSccc  aaaBBBccc  aaaBBbccc  aaaBbBccc  aaabBBccc  aaabBbccc  aaabbBccc  aaabbbccc

Отже, в цих виводах породжено ланцюжкі e, abc, aabbcc, aaabbbccc. Це дозволяє висунути припущення, що граматика G3 породжує мову L3={aⁿbⁿcⁿ | n³0}. Доведемо, що це дійсно так.

Теорема 4.1 L(G3)={aⁿbⁿcⁿ | n³0}.

Спочатку доведемо, що L(G3)Í{aⁿbⁿcⁿ | n³0}. Це доведення базується на наступній лемі, ідея якої полягає в тому, щоб сформулювати загальний вигляд ланцюжків в об’єднаному алфавіті, що виводяться в G3 (вигляд словоформ).

Лема 4.1 Нехай SÞ*_G3 a (aÎ(NÈT)*). Тоді існує n³0 таке, що

1) a=bgcⁿ , де bÎ{a,B}*, g=S або gÎ{b,B}*;

2) |a|_a=|a|_c=|a|_{b,B}= n.

Доведення леми: індукція по довжині виводу.

База індукції. Для виводу довжини 0 маємо, що n=0, a=S. Значить, a має вигляд bgc⁰ (b=e, g=S, c⁰=e) і тому |a|_a=|a|_c=|a|_{b,B}=0. Лема виконується.

Крок індукції. Нехай лема виконується для усіх виводів довжини k³0. Доведемо, що вона виконується для виводів довжини k+1.

Візьмемо довільний вивід SÞ_G3a₁Þ_G3 ... Þ_G3a_kÞ_G3a_k+1. Особливість виводів полягає в тому, що початкова послідовність SÞ_G3 a₁Þ_G3... Þ_G3 a_k буде виводом довжини k, і тому за індуктивним пропущенням для a_k виконується твердження леми. Іншими словами, є деяке n³0, таке що a_k=bgcⁿ та |a_k|_a=|a_k|_c=|a_k|_{b,B}=n. Безпосередній вивід a_kÞ_G3a_k+1 здійснюється за допомогою одного з правил P1, P2, P3, P4, P5. Розглянемо ці правила по черзі.

1. Нехай вивід a_kÞ_G3a_k+1 відбувся із застосуванням правила P1, тобто a_{k 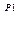G3}a_k+1. Тоді a_k має вигляд bScⁿ (bÎ{a,B}*), а a_k+1=baBScⁿ⁺¹. Тому a_k+1 має вигляд b¢Scⁿ⁺¹ (b¢Î{a,B}*), як того вимагає лема, і крім того, |a_k+1|_a=|a_k+1|_c=|a_k+1|_{b,B}= n+1. Для цього випадку лему доведено.  

2. Нехай вивід a_kÞ_G3a_k+1 відбувся застосуванням правила P2, тобто a_{k G3} a_k+1. Тоді a_k має вигляд bScⁿ (bÎ{a,B}*), а a_k+1=bcⁿ. Тому a_k+1 можна подати у вигляді bgcⁿ (g=e), як того вимагає лема, і крім того, |a_k+1|_a=|a_k+1|_c=|a_k+1|_{b,B}= n. Для цього випадку лему доведено.  

3. Нехай вивід a_kÞ_G3a_k+1 відбувся застосуванням правила P3. Оскільки a_k має загальний вигляд bgcⁿ, то правило P3 може бути застосовано лише для підланцужка b. Це правило не змінює ні загального вигляду a_k+1, ні кількісті символів, тому |a_k+1|_a=|a_k+1|_c=|a_k+1|_{b,B}= n. Для цього випадку лему доведено.  

4. Нехай вивід a_kÞ_G3a_k+1 відбувся застосуванням правила P4. Оскільки a_k має загальний вигляд bgcⁿ, то правило P4 може бути застосовано лише для підланцужка g (хоча можливо замінюване B є останнім символом b). Застосування правила не змінює ні загального вигляду a_k+1, ні кількісті символів, тому |a_k+1|_a=|a_k+1|_c=|a_k+1|_{b,B}= n. Для цього випадку лему доведено.  

5. При застосуванні правила P5 твердження леми також залишається справедливим.

Лему доведено._▄

Нехай тепер SÞ*_G3t (tÎT*). Оскільки t – ланцюжок в термінальному алфавіті, то він не містить нетерміналів, і за твердженням леми існує n³0 таке, що t=bgcⁿ, де bÎa*, gÎb* та|t|_a=|t|_c=|t|_b=n. Звідси випливає, що t=aⁿbⁿcⁿ. Іншими словами, будь який термінальний ланцюжок, що виводиться в G3, належить мові L3, тобто L(G3)ÍL3.

Доведемо тепер зворотне включення, тобто L3ÍL(G3). 

Для цього продемонструємо, як побудувати вивід ланцюжка aⁿbⁿcⁿ для довільного n. Використовуємо індукцію за n.

База індукції. Ланцюжок aⁿbⁿcⁿ (=e) отримуємо виводом S e.

Крок індукції. Нехай існує вивід слова aⁿbⁿcⁿ (n≥0), тобтоSÞ*_G3 aⁿbⁿcⁿ. Доведемо, що існує вивід слова aⁿ⁺¹bⁿ⁺¹cⁿ⁺¹, тобто SÞ*_G3 aⁿ⁺¹bⁿ⁺¹cⁿ⁺¹.

Відповідний вивід будуємо наступним чином. Спочатку до аксіоми застосуємо перше правило, а потім зробимо вивід слова aⁿbⁿcⁿ. Отримали наступний вивід: S 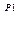aBScÞ*_G3aBaⁿbⁿcⁿc. Далі n разів застосовуємо правило P1, а потім – правило P2. Отримуємо ланцюжок (aB)ⁿcⁿ. Тепер n разів застосовуємо правило P3. Отримали ланцюжок  aaⁿBbⁿcⁿc(=aⁿ⁺¹Bbⁿcⁿ⁺¹). Після цього n разів застосовуємо правило P4. Отримали ланцюжок aⁿ⁺¹bⁿBcⁿ⁺¹. Нарешті, застосуванням правила P5 отримуємо ланцюжок aⁿ⁺¹bⁿ⁺¹cⁿ⁺¹.

Теорему 4.1 доведено. _▄

Наступним кроком у вивченні породжуючих граматик буде їх класифікація.

4.5 Ієрархія граматик Хомського

Дослідження будь-якого класу предметів, як правило, починається з їх класифікації. Це методологічне зауваження стосується і граматик. Однією з перших була класифікація, запропонована Н. Хомським. Суть цієї класифікації полягає в поступових обмеженнях, що накладаються на праві та ліві частини продукцій. Визначені Хомським чотири типи граматик виявились інваріантними відносно різних уточнень породжуючих граматик. Крім того, цим типам граматик природнім чином відповідають типи автоматів, що розпізнають (сприймають) формальні мови.

Визначення 4.20

· Граматиками типу 0 називають довільні породжуючі граматики загального виду, що не мають жодних обмежень на правила виводу.

• Граматиками типу 1 (нескорочуючими граматиками) називають породжуючі граматики, кожне правило яких має вигляд α→β, де |α|£|β| (αÎ(NÈT)*N(NÈT)*, βÎ(NÈT)⁺).
• Граматиками типу 2 (контекстно-вільними граматиками, КВ-граматиками) називають породжуючі граматики, кожне правило яких має вигляд A→β, де AÎN, βÎ(NÈT)*.
• Граматиками типу 3 (праволінійними граматиками) називають породжуючі граматики, кожне правило яких має вигляд A®αB або A®α, де A, BÎN, αÎTÈ{e}. До граматик типу 3 відносять і ліволінійні граматики, кожне правило яких має вигляд A®Bα або A®α, де A, BÎN, αÎTÈ{e}.

Приклад 4.12 Граматика G3 з попереднього підрозділу є граматикою типу 0. Якщо з цієї граматики видалити правило P2, вона стане граматикою типу 1, бо не буде скорочуючих правил. Граматика з правилами {S®AR, R®bRc, R®e, A®aA, A®e} є конктекстно вільною граматикою (типу 2), а її підграматика {A®aA, A®e} є праволінійною граматикою (типу 3).

Кожному типу граматик відповідають мови, яким будемо приписувати той же тип, що має граматика, яка її породжує. 

 

 

Малюнок 4.3. Співвідношення типів граматик

 

Малюнок 4.3 демонструє співвідношення типів граматик. Як бачимо, граматики типів 2 та 3 не є підкласами граматик типу 1. Це викликано тим, що наведені класи граматик мають скорочуючі правила виду A®e, які заборонені в граматиках типу 1. Як буде показано далі, ці відмінності не дуже позначаються на класах мов, породжуваних граматиками типів 2 та 3, і якщо ігнорувати порожній ланцюжок, то класи мов типів 3 та 2 будуть підкласами мов типу 1.

Перш ніж переходити до вивчення класів мов, покажемо, що без втрати виразної сили можна розглядати більш обмежений клас граматик, які називаються загально-конктестними граматиками. Цей клас видається більш природним для породження, ніж загальні породжуючі граматики.

Визначення 4.21

· Загально-контекстними називають породжуючі граматики, кожне правило яких має вигляд k₁ Ak₂→k₁βk₂, де AÎN, k₁, k₂, βÎ(NÈT)*. Ланцюжки k₁ і k₂ називають лівим та правим контекстом символу A у вказаному правилі.

• Контекстно-залежними називаються загально-конктестні граматики з нескорочуючими правилами, тобто правила мають вид k₁ Ak₂→k₁βk₂ , де βÎ(NÈT)⁺ (це означає, що|β|³1).

Контекстно-залежні граматики інколи називають граматиками безпосередньо складових (БС-граматиками). Ця назва пояснюється тим, що граматики цього класу співставляють породжуваним ними ланцюжкам системи (безпосередньо) складових, бо породження іде з одного нетерміналу, а конктекст при застосуванні правила не змінюється.

Слід сказати, що назва контекстно-залежних граматик не зовсім вдала, бо не підкреслює нескорочуваність правил граматики, а характеризує скоріш довільний клас конктекстних граматик. Це ж стосується і назви граматик безпосередньо складових.

Граматики типів 2 та 3 (будучи безконтекстними) безпосередньо є підкласами загально-контекстних граматик.

З визначень видно, що класи загально-контекстних та контекстно-залежних граматик є власними підкласами відповідно граматик типів 0 та 1. Разом з тим, відповідні класи мов співпадають, тобто використання лише конктекстних правил не обмежує породжувальну здатність граматик.

Доведемо цей факт співпадіння мов.

Нехай G₀=(N, T, P, S) – довільна породжуюча граматика типу 0. Побудуємо еквівалентну їй загально-контекстну граматику. Алгоритм побудови наступний.

1. Виділяємо термінальні символи, які входять до неконтекстних правил та вводимо нетермінали, які дублюють такі термінальні символи, тобто вводимо нові нетермінали N_a для кожного такого термінального символу aÎT.
2. Далі всі неконтекстні правила з P замінюємо на нові правила, в котрих замість термінальних символів стоять їх нетермінальні дублери. Добавляємо нові правила N_a®a. Очевидно, що отримана граматика G¢ еквівалентна початковій.
3. Побудуємо граматику G¢¢, яка буде контекстною та еквівалентною G¢. Спочатку пронумеруємо усі неконтекстні правила граматики G¢ (контекстні не змінюємо). Розглянемо неконтекстне правило G¢ з номером k виду a®b, де a = A₁A₂…A_n-1A_n, n>1. Це правило замінимо на наступну множину нових правил:

A₁A₂…A_n-1A_n® N_klA₂…A_n-1A_n

N_klA₂…A_n-1A_n® N_klA₂…A_n-1N_kr

N_klA₂…A_n-1 N_kr ® N_klA₃…A_n-1N_kr

N_klA3…A_n-1 N_kr ® N_klA4…A_n-1N_kr

…  …      …

N_klA_n-1N_kr ® N_klN_kr

N_klN_kr ® N_kpN_kr

N_kpN_kr ® N_kpb

N_kp®e.

(Коментар. Ідея побудови наведених правил полягає у наступному: спочатку виставляємо лівий N_kl та правий маркери N_kr вибраного правила, далі видаляємо всі інші символи лівої частини продукції, потім переходимо до породження правої частини, але перед цим вносимо про це інформацію за допомогою N_kp. Наприкінці породжуємо в контексті N_kp праву частину продукції, а сам символ N_kp видаляємо.)

Можна довести, що вказана послідовність правил еквівалентна одному початковому правилу. Дійсно, ця послідовність індукує (майже детерміновано) однозначний вивід. Тільки правило N_kp®e порушує однозначність. Але якщо його застосувати до правила N_kpN_kr®N_kpb, то не буде можливості позбавитись нетермінала N_kr. Тому справедлива наступна теорема.

---

Дата добавления: 2019-02-13; просмотров: 229; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!