Малюнок 2.7. Програма як діалектичне заперечення проблеми 10 страница

Наведений алгоритм можна уточнити за допомогою наступних індуктивних визначень.

1. P₀=P

2. P _i={B→aβ çє правила B→aA βÎР, A→eÎP _i-1} È R _i-1 (i=1,2, …).

Оскільки множина правил є скінченною, а праві частини нових правил коротші, то формула для визначення P_i задає монотонне за і відображення. Тому існує k (k³0), що P_k=P_k+1. Іншими словами, послідовність P₀, P₁, P₂, … стабілізується на k-му кроці. Покладемо P¢=P_k\{A→eÎP_k} .

Одержана граматика G¢=(N, T, P¢, S) породжує мову L(G)\ {e}.

Дійсно, кожен вивід в граматиці G, який не породжує порожнє слово, може бути промодельований в граматиці G¢, що легко доводиться індукцією по довжині виводу. Так само, можна промоделювати виводи в G¢ виводами в G, використовуючи замість модифікованих правил виду B→aβ початкові правила виду B→aAβ з подальшим виводом порожнього ланцюжка з A_▄

Приклад 4.20 Розглянемо граматику G з правилами

          S→aSb

          S→bSa

          S→e

Застосувавши до цієї граматики описаний метод видалення e-правил, отримаємо граматику G¢ з правилами

S→aSb

S→bSa

S→ab

S→ba

яка еквівалентна з точністю до порожнього ланцюжка граматиці G.

4.8.3 Нормальна форма Хомського

Визначення 4.36 Назвемо КВ-граматику G=(N, T, P, S) граматикою у нормальній формі Хомсього, якщо її правила мають вигляд S→e, A→a, A→BC для деяких A, B, CÎN, aÎT.

Лема 4.7 За кожною КВ-граматикою можна побудувати еквівалентну їй граматику у нормальній формі Хомського.

Доведення. Нехай дана КВ-граматика G=(N, T, P, S). Проведемо ряд перетворень цієї граматики так, що породжувана нею мова залишиться незмінною. Спочатку побудуємо еквівалентну граматику G¢=(N¢, T¢, P¢, S¢) без e-правил.

Далі замінимо у всіх правилах кожен термінальний символ a на новий нетермінальний символ N(a) і додамо до множини P правила N(a)→a для всіх aÎT.

Видалимо правила вигляду A→A₁A₂…A_n, де n >2, замінюючи його на наступний ряд нових правил A→A₁N(A₂…A_n), N(A₂…A_n)→ A₂N(A₃…A_n), …, N(A_n-1…A_n)→ A_n-1A_n (при цьому додаються нові нетермінальні символи N(A₂…A_n), N(A₃…A_n), …, N(A_n-1…A_n)).

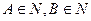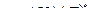Якщо для деяких  і  множина  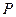містить правила 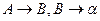, але не містить правила 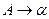, то додамо це правило в 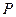. Повторюємо цю процедуру, доки можливо. Після цього видалимо із множини  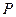всі правила вигляду .

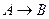Нарешті, змінимо S на S¢,  та додамо правила S¢→e, S →S¢ в тому випадку, коли мова L(G) містить порожній ланцюжок. 

Приклад 4.21 Граматика 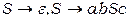 еквівалентна наступній граматиці в нормальній формі Хомського: , , , , .

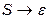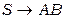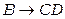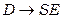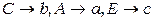4.8.4 Нормальна форма Грейбах

Визначення 4.37 КВ-граматику G=(N, T, P, S) будемо називати граматикою в нормальній формі Грейбах, якщо її правила мають вигляд A→aa (aÎT, aÎ(NÈT)*), тобто кожне правило починається з термінального символу.

Сформулюємо без доведення наступне твердження.

Лема 4.8 За кожною КВ-граматикою можна побудувати e-еквівалентну їй (з точністю до порожнього ланцюжка) граматику у нормальній формі Грейбах.

Зауважимо, що наявність нормальної форми Грейбах дозволяє досить легко за кожною граматикою побудувати еквівалентний їй недетермінований магазинний автомат. Також в таких граматиках довжина виводу термінального ланцюжка не перевищує його довжину.

Приклад 4.22 Граматика 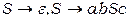 еквівалентна наступній граматиці в нормальній формі Грейбах: , .

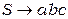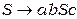4.8.5 Рекурсивні нетермінали

Визначення 4.38 Нетермінал А Î N КВ-граматики назвемо рекурсивним (самовставним, циклічним), якщо існує вивід виду АÞ*aАb. Якщо такого виводу немає, то нетермінал називають нерекурсивним.

Лема 4.9 Якщо КВ-граматика G не має рекурсивних нетерміналів, то мова L(G) скінченна.

Дійсно, в цьому випадку може бути лише скінченна кількість виводів, тому породжується лише скінченна мова.

Зауважимо, що зворотнє твердження не є справедливим для довільної граматики, бо може бути рекурсивний нетермінал, що породжує скінченну мову. Це можливо для рекурсивного нетерміналу, коли є вивід АÞ*aАb, але завжди з a та b породжуються порожні ланцюжки: aÞ*e та bÞ*e.  Крім того, рекурсивні недосяжні або непродуктивні рекурсивні нетермінали не впливають на породжувану мову.

Приклад 4.23 Розглянемо граматику, множина Р якої складається з наступних правил виведення:

          S→AB

       A→C

          A→a

          B→b

          C→A

Мова, породжена цією граматикою, складається з єдиного ланцюжка ab. Але нетермінали A та C є рекурсивними.

Отже, наведена лема дозволяє сформулювати необхідну умову породження КВ-граматикою нескінчених мов: нескінчена мова може породжуватися лише граматикою з рекурсивними нетерміналами. Але ця умова, як показує приклад, не є достатньою.

Для нескінченних мов має місце наступне твердження.

Лема 4. 10 Нехай граматика G=(N, T, P, S) породжує нескінченну мову. Тоді існує суттєвий рекурсивний нетермінал A такий, що має місце АÞ*t₁Аt₂, де t₁,t₂ÎT* та |t₁t₂|³1.

Ця лема буде використовуватись для доведення властивостей КВ-мов.

 

4.9 Властивості контекстно-вільних мов

В цьому розділі розглянемо властивості КВ-мов, тобто структуру ланцюжків, виразну потужність КВ-мов та їх замкненість відносно операцій над формальними мовами.

Спочатку сформулюємо для КВ-мов аналог твердження (Лема 4.10), яке характеризувало властивості КВ-граматик. 

Лема 4.11 (лема про розростання, лема про накачку). Нехай 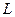– КВ-мова над алфавітом T. Тоді знайдеться таке натуральне число k, що для довільного ланцюжка tÎL довжини не менше k знайдуться ланцюжкі u, v, t₁, t₂, x ÎT*, для яких вірно u t₁ x t₂ v=t, |t₁t₂|³1, |t₁ x t₂|£k та u t₁ ⁱ x t₂ ⁱ vÎL для всіх i=0,1,….

Ідея доведення полягає в тому, що для породження мови  L розглядається граматика у нормальній формі Хомського (нескорочуюча граматика). Тоді для достатньо довгих виводів можна виділити рекурсивний нетермінал A такий, що має місце АÞ*t₁Аt₂, де t₁,t₂ÎT* та |t₁t₂|³1 (дивись попереднью лему). Звідси і буде випливати твердження леми.

 

4.10 Операції над формальними мовами

Лема 4.12 Мова L3={aⁿbⁿcⁿ | n³0} не є КВ-мовою.

Доведення. Якби мова L3 була б КВ-мовою, то тоді існували б ланцюжи u, v, t₁, t₂, x Î{a,b,c}* такі, що u t₁ ⁱ x t₂ ⁱ vÎL3 для всіх i=0,1,…. Зрозуміло, що t₁ (так само як і t₂) не може складатися з різних символів (інакше для деякого i ланцюжок u t₁ ⁱ x t₂ ⁱ v не буде належати L3. Але якщо t₁ складається лише з одного символу, то збільшуючи i можна порушити баланс символів a,b,c. Тому мова L3 не може бути КВ-мовою.

Далі почнемо розгляд властивостей КВ-мов відносно теоретико-множинних операцій.

 Лема 4.13 Клас КВ-мов замкнений відносно об’єднання.

Дійсно, нехай КВ-мови L₁ та L₂ породжені граматиками G₁=(N₁, T, P₁, S₁) та G=(N₂, T, P₂, S₂) відповідно. Задамо граматику G, отриману в результаті об’єднань граматик G₁ та G₂, наступним чином:

· перейменуємо (якщо це потрібно) множини нетерміналів N₁ і N₂ так, щоб N₁∩N₂=Æ, та додамо новий нетермінал S;

· об’єднаємо множини правил P₁ і P₂, додаючи два нових правила S→S₁ та S→S₂.

Таким чином отримуємо граматику G=(N₁ÈN₂È{S}, T, P₁ÈP₂È{S→S₁, S→S₂}, S), яка складається з усіх правил граматик G₁ та G₂ з перейменованими множинами нетерміналів так, що N₁∩N₂=Æ, та з доданих правил S→S₁, S→S₂. З побудови очевидно, що G породжує всі слова з мов L₁ та L₂. Доведемо, що вона не породжує інших слів.

Згідно твердження (Лема 4.) перейменування нетерміналів не змінює породжувану мову. Оскільки найпершим правилом у виводі є S→S₁ або S→S₂, то далі ми продовжуємо вивід або для S₁, або для S₂, породжуючи слова лише з мови L₁ або L₂ відповідно. Отже, L належить класу КВ-мов.

Лема 4.14 Клас КВ-мов не замкнений відносно перетину.

Для доведення цього факту достатньо розглянути приклад.

Візьмемо мови L1={aⁿb^mc^m | n,m³0} та L2={aⁿbⁿc^m | n,m³0}. Ці мови є КВ-мови. Однак мова L₁∩L₂={aⁿbⁿcⁿ| n≥0}= L3 не є КВ-мовою.

Лема 4.15 Клас КВ-мов не замкнений відносно доповнення.

Твердження леми випливає з попередньої леми, оскільки, в силу законів де Моргана, будь-який клас мов, замкнений відносно об’єднання та доповнення, має бути замкненим відносно перетину. Тобто, з припущення замкненості класу КВ-мов відносно доповнення випливає замкненість відносно перетину, що суперечить попередній лемі.

Приклад 4.24 Побудуємо КВ-граматику, яка задає мову, доповнення до якої не буде КВ-мовою.

Ідея побудови випливає з лем 4.14 та 4.15. Візьмемо мову L3={aⁿbⁿcⁿ| n≥0}, яка не є КВ-мовою. Покажемо, що її доповнення – мова 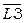є КВ-мовою. Оскільки 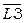= = 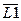È 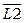, то спочатку доведемо, що доповнення мов L1 та L2, тобото мови  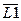та 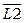,  є КВ-мовами. Дійсно, L1, L2 Í a*b*c*. Остання мова є регулярною, тому її доповнення  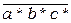= ({a,b,c}*\ a*b*c*) також є регулярною мовою. Ця мова містить слова, які мають заборонені комбінації двох символів, тобто комбінації, які порушують порядок слідування символів у мовах L1 та L2. Порядок слідування є наступним:

· літера a передує літері b, або літері c;

· літера b передує літері c.

Заперечення цих тверджень дає наступні комбіції: ba, ca, cb. Тому ({a,b,c}*\ a*b*c*)={a,b,c}*ba{a,b,c}*È{a,b,c}*ca{a,b,c}*È{a,b,c}*cb{a,b,c}*. Ця мова задається наступною граматикою:

S®R ba R |R ca R |R cb R

R®e|aR | bR | cR

Отже, 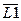={a,b,c}*\L1=({a,b,c}*\ a*b*c*)È (a*b*c*\L1). Покажемо, що мова (a*b*c*\L1) є КВ-мовою. В ланцюжках цієї мови кількість літер b не співпадає з кількістю літер c. Ця мова задається граматикою:

S®AbBE

S®AEcC

E ®e| bEc

A®e| aA

B®e| bB

C®e| cC

Аналогічно будується граматика другої мови 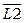={a,b,c}*\L2=({a,b,c}*\ a*b*c*)È (a*b*c*\L2), в ланцюжках якої кількість літер a не співпадає з кількістю літер b:

S®Q b B C

S® A aQ C

Q ®e| aQb

A®e| aA

B®e| bB

C®e| cC

Об’єднуючи три граматики (а це можна зробити, бо колізії нетерміналів не відбувається), отримуємо наступну граматику:

S®R ba R |R ca R |R cb R | AbBE | AEcC | Q b B C | A aQ C

R®e|aR | bR | cR

E ®e| bEc

Q ®e| aQb

A®e| aA

B®e| bB

C®e| cC

Ця граматика породжує КВ-мову, але її доповнення не є КВ-мовою. _▄

Розглянемо тепер деякі специфічні операції над мовами, які відповідають більш конкретному рівню абстракції, який трактує ланцюжки як послідовності символів.

Лема 4.16 Клас КВ-мов замкнений відносно конкатенації.

Дійсно, нехай КВ-мови L₁ та L₂ породжені граматиками G₁=(N₁, T, P₁, S₁) та G₂=(N₂, T, P₂, S₂) відповідно. Будемо вважати, що N₁∩N₂=Æ. Візьмемо символ SÏN₁ÈN₂. Тоді мова L₁∙L₂={w₁w₂| w₁ÎL₁, w₂ÎL₂} буде породжена КВ-граматикою G=(N₁ÈN₂È{S}, T, P₁ÈP₂È{S→S₁S₂}, S). Це випливає з того, що вивід будь-якого ланцюжка починається з доданого правила S→ S₁S₂, а далі будується з правил P₁ та P₂, які виводять лише слова з мов L₁ та L₂ відповідно.

Лема 4.17 Клас КВ-мов замкнений відносно ітерації.

Дійсно, нехай КВ-мова L породжена граматикою G=(N, T, P, S). Тоді мова L* буде породжена КВ-граматикою G=(NÈ{S¢}, T, PÈ{ S¢→S¢S, S¢→ε}, S¢), де S¢ÏN. Це випливає з того, що вивід будь-якого слова починається з доданого правила S¢→S¢S, що дозволяє породжувати будь-яку кількість ланцюжків з мови L.

---

Дата добавления: 2019-02-13; просмотров: 240; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!