Зображення декартового добутку двох числових множин на координатній площині
Поняття відношення. Властивості відношень. Способи задання відношень
Відношенням (n-місним відношенням) в теорії множин називається підмножина декартового степеня Mn деякої множини M. Кажуть також, що елементи a1,a2,...,an∈M знаходяться у відношенні R, якщо кортеж (a1,a2,...,an)∈R.
До відношень можна застосовувати теоретико-множинні операції і алгебру множин.
Поняття відношення є певним теоретико-множинним узагальненням відомого з елементарної арифметики набору таких відношень, як "=" (дорівнює) або "<" (менше). Поняття відношення і операцій з ними в практичних застосуваннях грає ключову роль в побудові реляційних моделей систем управління базами даних.
В математичній літературі часто не розрізняють поняття відношення та відповідності між множинами (тобто, в такому випадку, відношення можуть мати місце між різними множинами). В цій енциклопедії поняття відношення на множині та відношення між множинами (відповідності між множинами) розрізняються, якщо інше не вказано окремо.
Для задання відношень можна користуватись тими ж способами, що і при
заданні множин. Наприклад, якщо множина M скінченна, то довільне
відношення R на M можна задати списком пар елементів, які знаходяться у
відношенні R.
В математиці бінарне відношення R на множині X є рефлексивним, якщо для кожного a ∈ X виконується aRa, тобто
|
|
|
Властивість рефлексивності: матриця рефлексивного відношення характеризується тим, що всі елементи головної діагоналі рівні 1; граф — тим, що при кожен елемент має петлю — дугу (х, х).
Якщо ця умова не виконана ні для якого з елементів множини 
, тоді відношення 
називається антирефлексивним.
Якщо антирефлексивне відношення задано матрицею, то всі елементи її головної діагоналі дорівнюють нулю. Граф такого відношення характеризується тим, що не має жодної петлі — немає дуг вигляду (х, х).
Формально антирефлексивність відношення 
визначається як: 
.
Якщо умова рефлексивності виконана не для всіх елементів множини , тоді кажуть, що відношення 
нерефлексивне.
Приклади рефлексивних відношень [ред.]
"дорівнює"
"менше або дорівнює"
"більше або дорівнює"
"є підмножиною або дорівнює"
Приклади відношень, що не є рефлексивними [ред.]
"не дорівнює"
"менше"
"більше"
"є підмножиною"
Відношення еквівалентності
Відно́шення еквівале́нтності ( 
) на множині 
— це бінарне відношення для якого виконуються наступні умови:
Рефлексивність
Симетричність
Транзитивність
Запис вигляду « 
» читається як « 
еквівалентно 
».
|
|
|
Класом еквівалентності 
елемента 
називається підмножина елементів, еквівалентних . З зазначеного визначення випливає що, якщо 
, то 
.
Множина всіх класів еквівалентності позначається 
.
Для класу еквівалентності елемента 
використовується наступне позначення: 
, 
, 
.
Множина класів еквівалентності по відношенню є розбиттям множини.
Приклади відношень еквівалентності[ред.]
Найбільш наочний і всім знайомий приклад відношення еквівалентності — поділ учнів школи на класи.
Відношення рівності (« ») тривіальне відношення еквівалентності на довільній множині, зокрема на множині дійсних чисел.
Порівняння по модулю, («а ≡ b (mod n)»).
В Евклідовій геометрії
Відношення конгруентності (« 
»).
Відношення подібності (« 
»).
Відношення паралельності прямих (« 
»).
Відношення рівнопотужності множин є еквівалентністю.
Еквівалентність функцій в Математичному аналізі:
кажуть що функція 
еквівалентна функції 
при 
, якщо вона може бути представлена у вигляді: 
, де 
при . В даному випадку пишуть 
, при . Якщо 
при 
, еквівалентність функції та 
при , очевидно, рівносильна відношенню 
.
Ще один важливий, життєвий випадок: Коли лікар виписує ліки, в рецепті він записує класи еквівалентних ліків. Він не може вказати конкретний приклад абсолютно конкретний екземпляр упаковки таблеток або ампул. Таким чином, всі ліки розбиті на класи відношенням еквівалентності.
|
|
|
Відношення порядку
Відно́шення поря́дку в математиці — бінарне відношення, яке є транзитивним та антисиметричним.
(транзитивність),
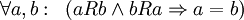(антисиметричність).
Відношення порядку називається нестрогим, якщо воно рефлексивне
.
І навпаки, відношення строгого порядку є антирефлексивним
.
Відношення порядку називається повним (лінійним), якщо
(повне відношення).
Повнота (лінійність) відношення порядку означає його рефлексивність, тому такий порядок завжди нестрогий.
Якщо умова повноти не виконується, і порядок є нестрогим, то відношення називають відношенням часткового порядку.
Зазвичай відношення строгого порядку (повного чи часткового) позначається знаком <, а відношення нестрогого порядку знаком 
.
Дата добавления: 2019-02-13; просмотров: 437; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!