Дедуктивні міркування. Найпростіші схеми дедуктивних міркувань.
• Дедуктивні міркування. Довести теорему  - значить встановити логічним шляхом, що завжди, коли виконується властивість А, буде виконуватись і властивість В. доведення в математиці обладає рядом особливостей. Часто воно проводиться за правилами логіки без яких-то посилань на наглядність і дослід. В основі доведення лежить міркування – логічна операція, в результаті якої із одного чи декількох взаємозв‘язаних по змісту тверджень отримаємо твердження, яке містить нові (по відношенню до заданих) знання. В якості приклада розглянемо міркування першокласника, якому необхідно встановити відношення «менше» між числами 7 і 8. учень говорить: «
- значить встановити логічним шляхом, що завжди, коли виконується властивість А, буде виконуватись і властивість В. доведення в математиці обладає рядом особливостей. Часто воно проводиться за правилами логіки без яких-то посилань на наглядність і дослід. В основі доведення лежить міркування – логічна операція, в результаті якої із одного чи декількох взаємозв‘язаних по змісту тверджень отримаємо твердження, яке містить нові (по відношенню до заданих) знання. В якості приклада розглянемо міркування першокласника, якому необхідно встановити відношення «менше» між числами 7 і 8. учень говорить: « 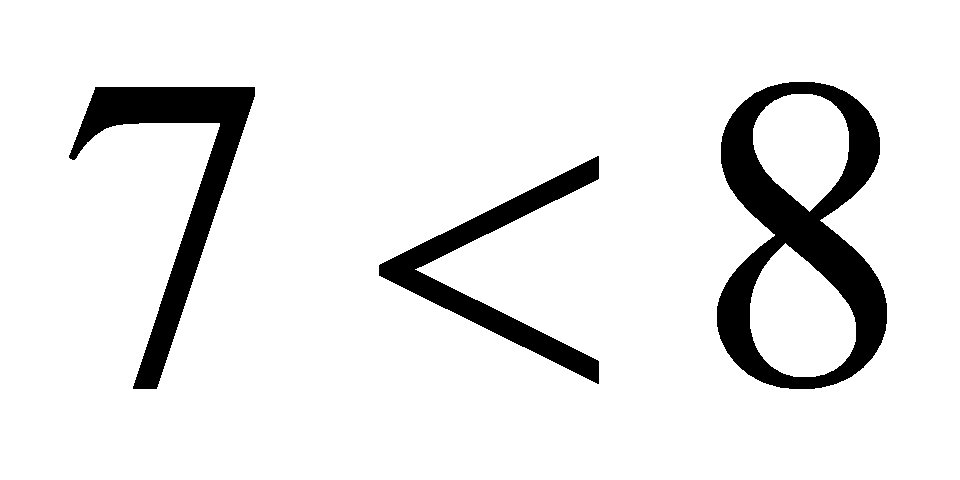 , тому що 7 при рахунку називають раніше, ніж 8». На які ж факти він опирався, стверджуючи це. По-перше, якщо число а при рахунку називають раніше числа в, то
, тому що 7 при рахунку називають раніше, ніж 8». На які ж факти він опирався, стверджуючи це. По-перше, якщо число а при рахунку називають раніше числа в, то 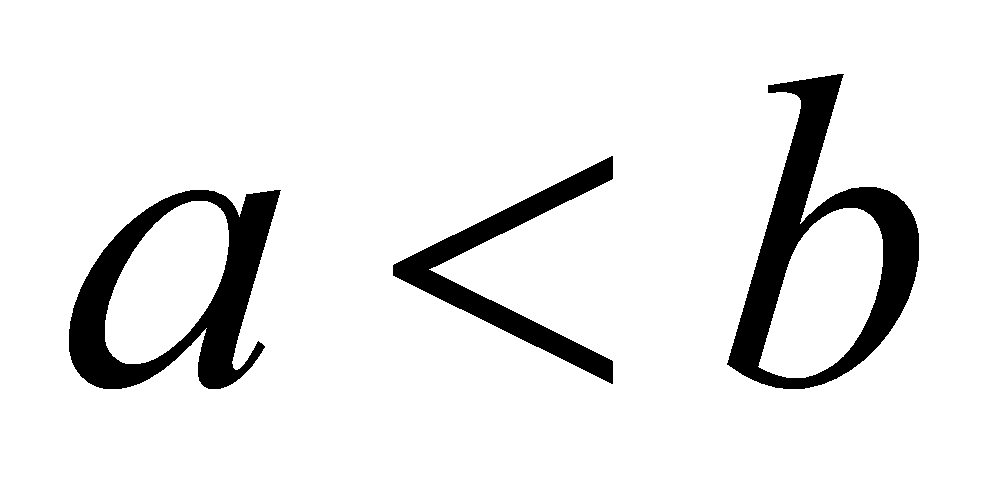 для будь-яких натуральних чисел. І по-друге, 7 при рахунку називають раніше, ніж 8. перше твердження носить загальний характер, так як містить квантор спільності, його називають загальною посилкою. Друге твердження стосується конкретних чисел 7 і 8, відображає частинний випадок, його називають частковою посилкою. З двох посилок і випливає новий факт
для будь-яких натуральних чисел. І по-друге, 7 при рахунку називають раніше, ніж 8. перше твердження носить загальний характер, так як містить квантор спільності, його називають загальною посилкою. Друге твердження стосується конкретних чисел 7 і 8, відображає частинний випадок, його називають частковою посилкою. З двох посилок і випливає новий факт 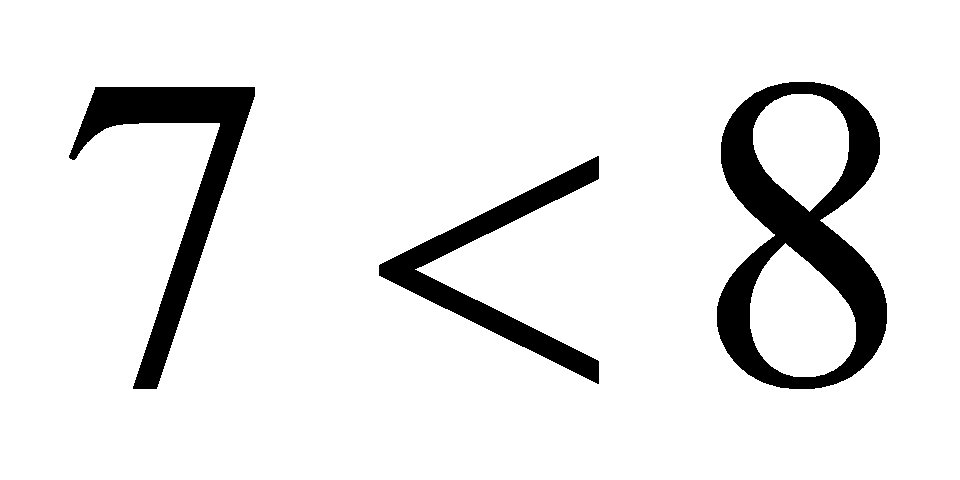 , його називають висновком. Міркування, між посилками і висновком якого має місце відношення слідування, називають дедуктивним. Іншими словами, міркування є дедуктивним, якщо за допомогою його з істинних посилок не можна отримати хибний висновок. Інакше міркування не являється дедуктивним.
, його називають висновком. Міркування, між посилками і висновком якого має місце відношення слідування, називають дедуктивним. Іншими словами, міркування є дедуктивним, якщо за допомогою його з істинних посилок не можна отримати хибний висновок. Інакше міркування не являється дедуктивним.
|
|
|
Найпростіші схеми дедуктивних міркувань. Вважають, що в основі кожного дедуктивного міркування лежить певне правило висновку. 1) Правило висновку (  і
і 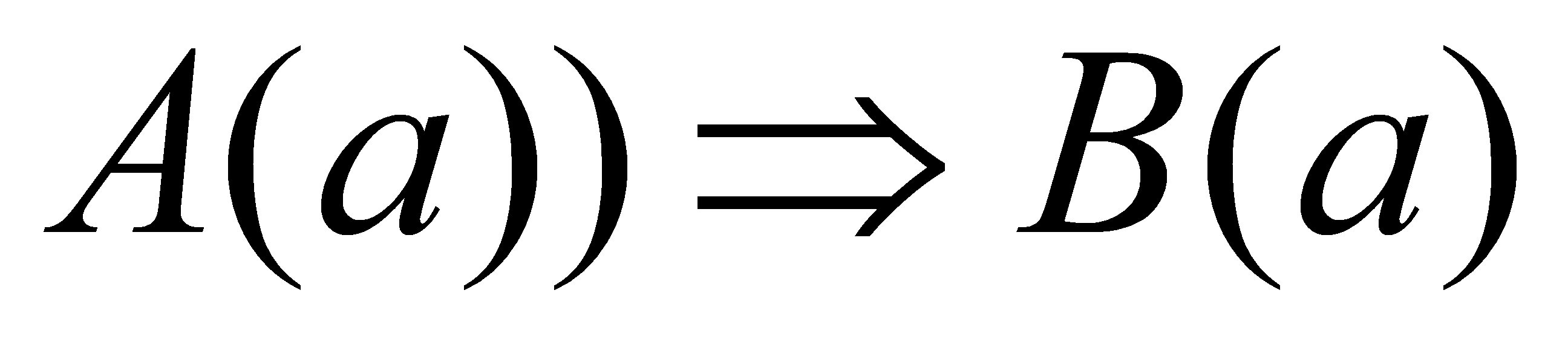 , де
, де  - загальна посилка,
- загальна посилка, 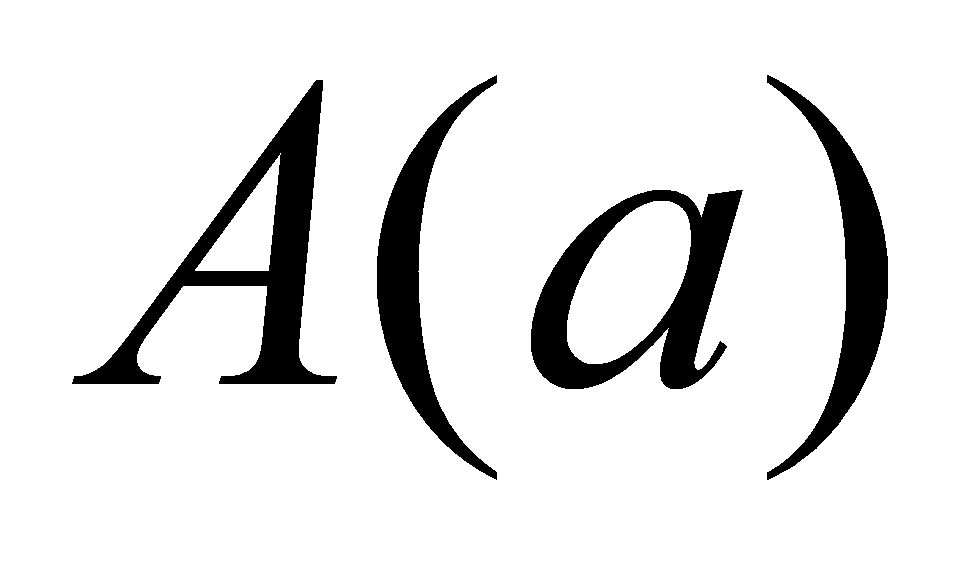 - часткова посилка і
- часткова посилка і 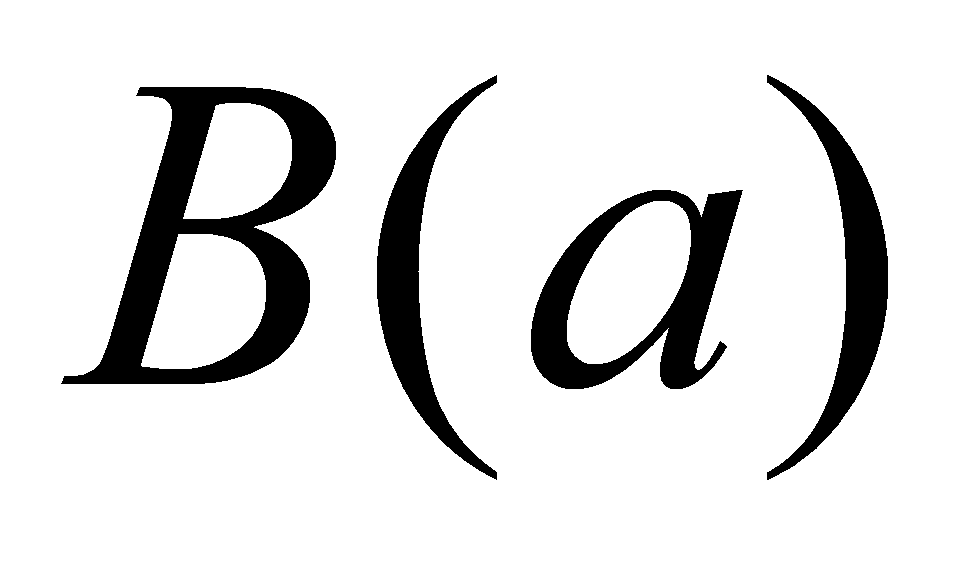 - висновок. 2) Правило заперечення
- висновок. 2) Правило заперечення 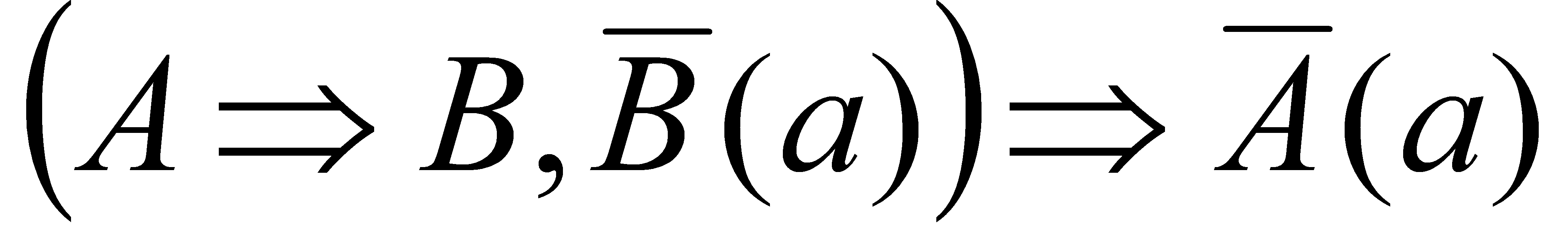 . 3) Правило силогізму
. 3) Правило силогізму 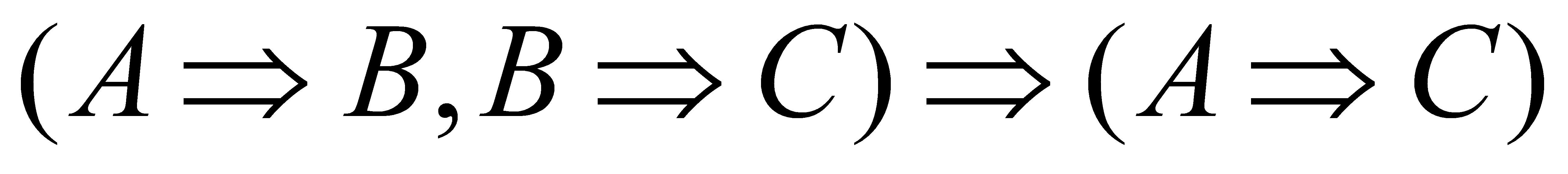 . Застосування цих правил гарантує, що міркування буде дедуктивним, тобто дозволяє з істинних посилок виводити істинні висновки. Наприклад, 1) Всі числа, запис яких закінчується нулем, діляться на 5; число не ділиться на 5, значить, його запис не закінчується 0. 2) Якщо натуральне число кратне 8, то воно кратне 4; якщо натуральне число кратне 4, то воно кратне 2; значить, якщо число кратне 8, то воно кратне 2. 3) Якщо запис числа закінчується нулем, то воно ділиться на 5; число не закінчується нулем, значить, воно не ділиться на 5.
. Застосування цих правил гарантує, що міркування буде дедуктивним, тобто дозволяє з істинних посилок виводити істинні висновки. Наприклад, 1) Всі числа, запис яких закінчується нулем, діляться на 5; число не ділиться на 5, значить, його запис не закінчується 0. 2) Якщо натуральне число кратне 8, то воно кратне 4; якщо натуральне число кратне 4, то воно кратне 2; значить, якщо число кратне 8, то воно кратне 2. 3) Якщо запис числа закінчується нулем, то воно ділиться на 5; число не закінчується нулем, значить, воно не ділиться на 5.
Неповна індукція. Способи доведення істинності висловлень.
Відомо, що 15 ділиться на 5, 25 ділиться на 5, 35 і 95 діляться на 5. враховуючи це, робимо висновок, що будь-яке число, запис якого закінчується цифрою 5, ділиться на 5. В розглянутому міркуванні на основі ряду часткових випадків робимо висновок загальний. Такі міркування називають неповною індукцією. Неповна індукція представляє собою таке міркування, при якому на основі того, що деякі об‘єкти сукупності мають певні властивості, робиться висновок про те, що ці властивості притаманні всім об‘єктам цієї сукупності. Висновки, отримані при неповній індукції, можуть бути як істинними, так і хибними. Так висновок про те, що кожне число, запис якого закінчується цифрою 5, ділиться на 5, істинний. А твердження «при будь-якому натуральному числі 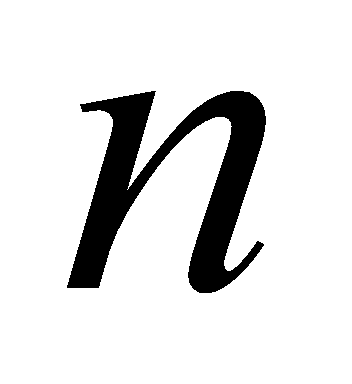 значення виразу
значення виразу 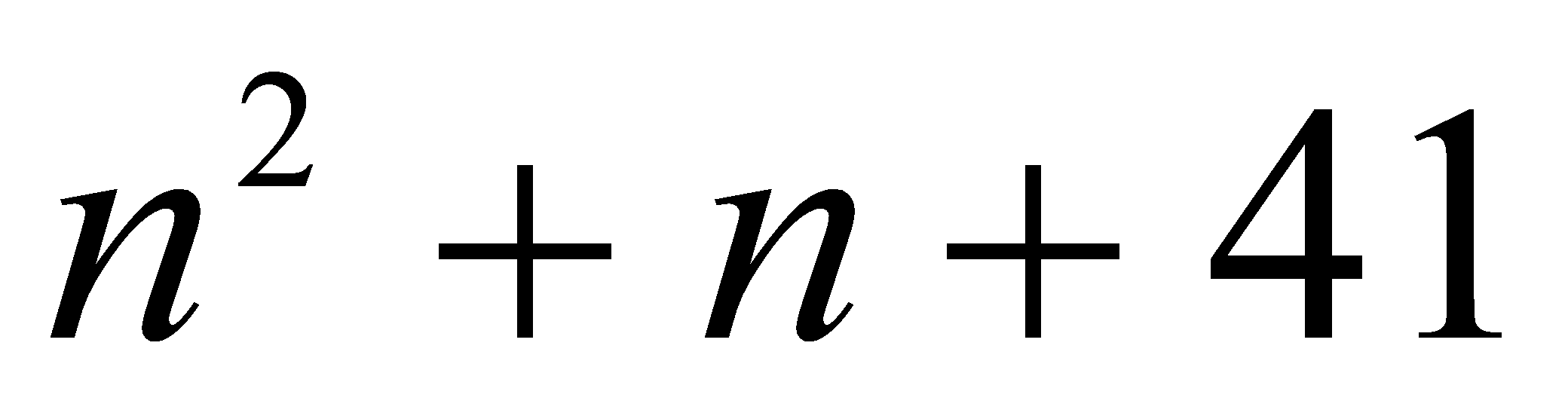 є просте число» хибне. Дійсно, якщо
є просте число» хибне. Дійсно, якщо 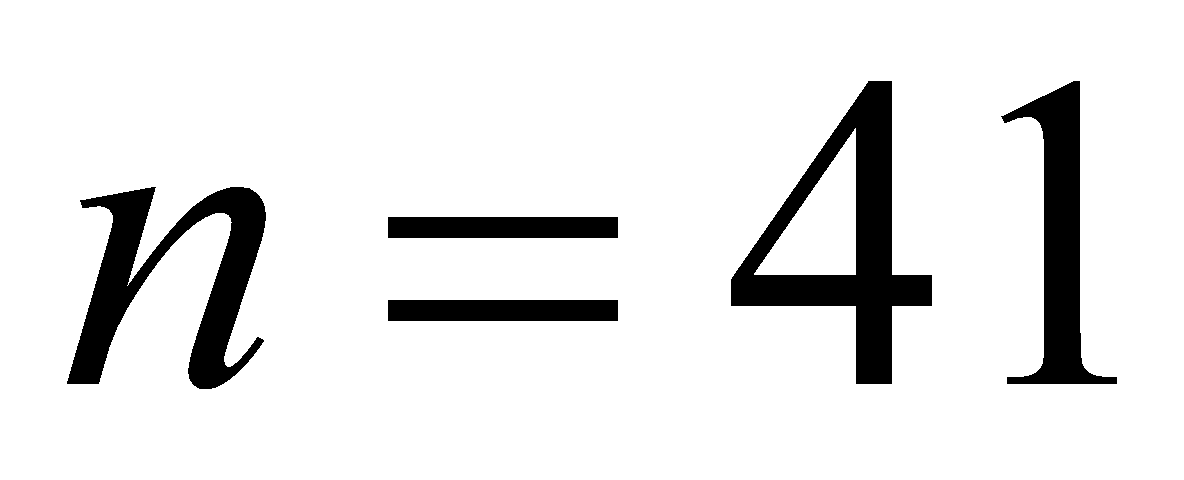 , то отримаємо значення
, то отримаємо значення 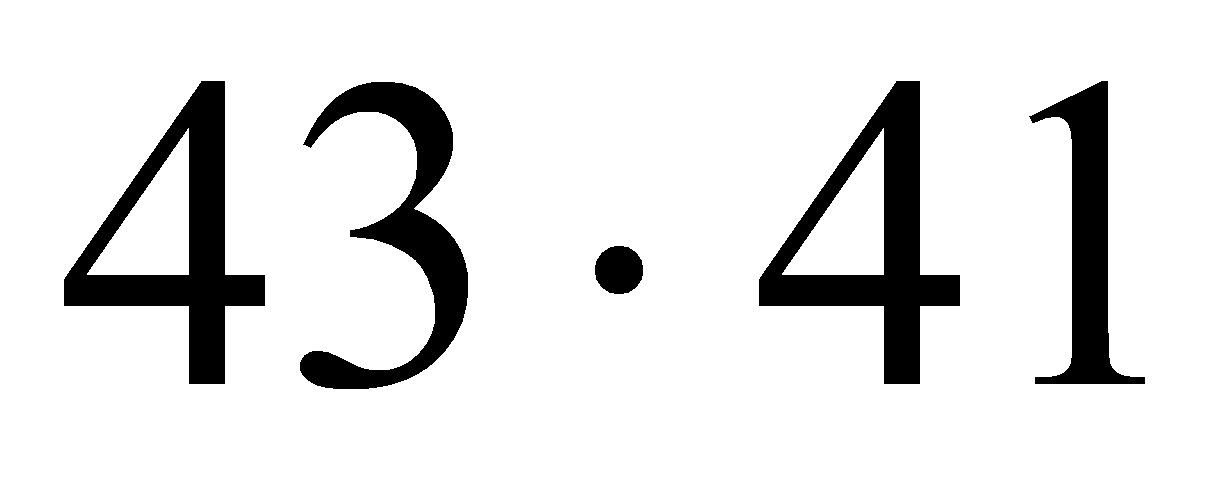 , тобто даний вираз є складовим числом. До висновків, отриманих за допомогою неповної індукції, треба відноситись критично. Ці висновки носять характер гіпотези, догадки, яку слідує або довести (дедуктивним методом), або спростити. Таким чином, в процесі пізнань дедуктивні і індуктивні міркування виявляються взаємозв‘язаними. При тому що індуктивні міркування не завжди приводять до правильних висновків, роль їх в вивченні математики і інших науках дуже велика. В ході індуктивних міркувань формується вміння бачити загальне в конкретних, часткових випадках, висловлювати догадки.
, тобто даний вираз є складовим числом. До висновків, отриманих за допомогою неповної індукції, треба відноситись критично. Ці висновки носять характер гіпотези, догадки, яку слідує або довести (дедуктивним методом), або спростити. Таким чином, в процесі пізнань дедуктивні і індуктивні міркування виявляються взаємозв‘язаними. При тому що індуктивні міркування не завжди приводять до правильних висновків, роль їх в вивченні математики і інших науках дуже велика. В ході індуктивних міркувань формується вміння бачити загальне в конкретних, часткових випадках, висловлювати догадки.
|
|
|
10.Поняття множини та та елемента множини. способи задання множин.В математиці часто приходиться розглядати певні групи об‘єктів як єдине ціле: числа від 1 до 10, натуральні числа, трикутники. Всі ці різноманітні сукупності називають множинами. Поняття множини являється одним з основних понять математики і тому не має означення через інші поняття. Його можна пояснити на прикладах: множина учнів класу, множина букв алфавіту, натуральні числа. В математиці розглядають множину, яка містить один об‘єкт, або не містить жодного елемента, яка називається пустою. Об‘єкти, з яких складається множина, називають його елементами. Часто приходиться з‘ясовувати належність елемента до розглянутої множини. Множини бувають скінчені і нескінчені. Скінченою множиною називають таку, елементи якої можна перерахувати. Нескінченими являються і множини чисел.
|
|
|
Способи завдання множин. Вважають, що множина визначається своїми елементами, тобто множина задана, якщо про будь-який об‘єкт можна сказати, належить він цій множині чи не належить. Множину можна задати, перерахувавши всі його елементи. Наприклад, 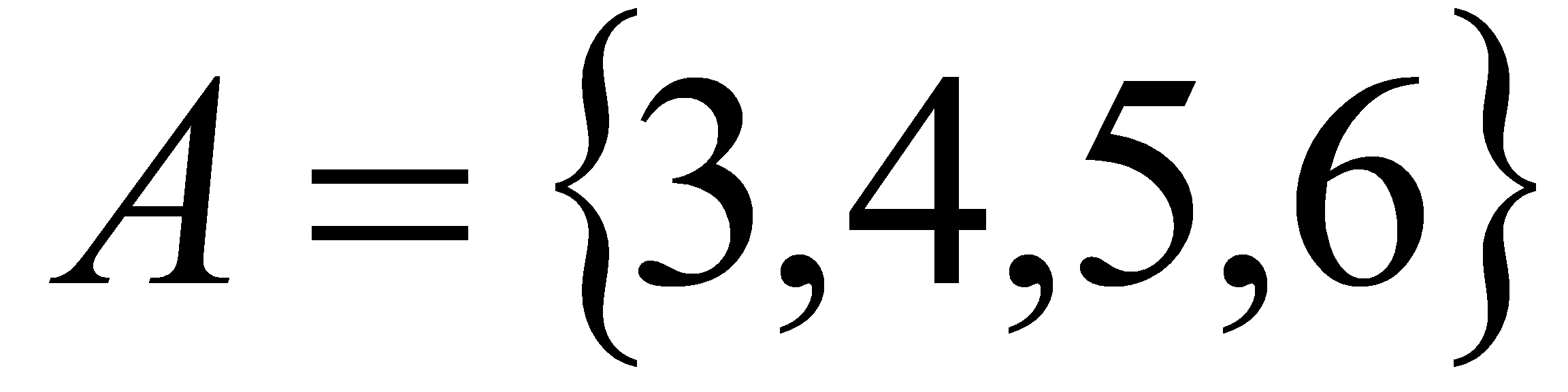 . Якщо множина нескінчена, то її елементи перерахувати не можна. В таких випадках вказують характеристичну властивість його елементів. Характеристична властивість – це така властивість, якою володіє кожний елемент, який належить множині, і не володіє жоден з елементів, який йому не належить. Для того щоб задати деяку множину, достатньо або перерахувати всі його елементи, або вказати характеристичну властивість його елементів. Наприклад, множина А натуральних чисел, менших 7, задана вказанням характеристичної властивості його елементів, можна задати і так:
. Якщо множина нескінчена, то її елементи перерахувати не можна. В таких випадках вказують характеристичну властивість його елементів. Характеристична властивість – це така властивість, якою володіє кожний елемент, який належить множині, і не володіє жоден з елементів, який йому не належить. Для того щоб задати деяку множину, достатньо або перерахувати всі його елементи, або вказати характеристичну властивість його елементів. Наприклад, множина А натуральних чисел, менших 7, задана вказанням характеристичної властивості його елементів, можна задати і так: 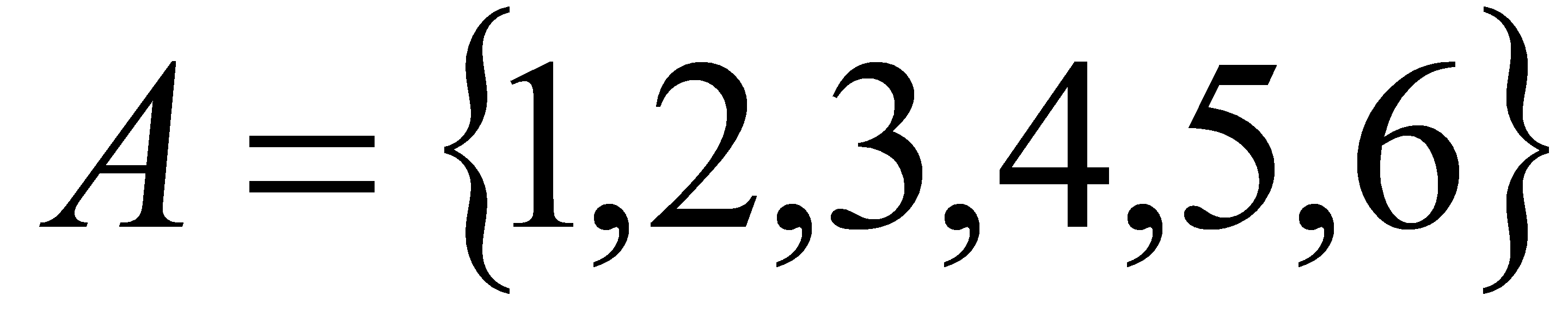 , тобто перерахував його елементи.
, тобто перерахував його елементи.
|
|
|
Теоретико-множинні операції
 доповнення
доповнення
 об'єднання
об'єднання
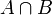 перетин
перетин
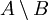 різниця
різниця
 симетрична різниця
симетрична різниця
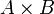 декартів добуток
декартів добуток
Дата добавления: 2019-02-13; просмотров: 496; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
