Тема 8. Управління фінансовими інвестиціями.
Особливості і форми здійснення фінансових інвестицій. Фінансовий ринок та його розвиток в Україні. Формування портфелю фінансових інвестицій. Політика управління фінансовими інвестиціями.
Питання для самостійного вивчення:
1. Фінансовий ринок та його розвиток в Україні.
2. Класифікація та особливості інструментів ринку цінних паперів.
3. Характеристика інвестиційних якостей основних цінних паперів.
4. Управління портфелем фінансових інвестицій.
Тема 9. Управління формуванням інвестиційних ресурсів.
Суть інвестиційних ресурсів та їх види. Формування інвестиційних ресурсів. Ресурси інвестиційної стратегії підприємства. Методика розрахунку потреби в інвестиційних ресурсах. Оптимізація структури інвестиційних ресурсів.
Питання для самостійного вивчення:
1. Інвестиційний капітал.
2. Джерела фінансування інвестиційної діяльності.
3. Процес розміщення інвестиційних ресурсів підприємства.
4. Оцінка вартості інвестиційних ресурсів.
5. Оптимізація структури джерел фінансування інвестиційної діяльності.
Тематика рефератів:
1. Проблеми вивчення та оцінки інвестиційної привабливості галузі.
2. Проблеми вивчення та оцінки інвестиційної привабливості регіону (на прикладі Полтавської області).
3. Дослідження інвестиційної привабливості окремого підприємства.
4. Загальні поняття та цілі державного регулювання інвестиційної діяльності.
|
|
|
5. Методи державного регулювання інвестиційної діяльності.
6. Основні принципи інвестиційної політики України.
7. Інвестиційний потенціал країни, інвестиційний комплекс.
8. Інвестиційної стратегія і політика України, інвестиційні пріоритети та фактори, які їх визначають.
9. Макроекономічні показники розвитку інвестиційного ринку в Україні.
10. Показники оцінки інвестиційної привабливості підприємства.
11. Грошові відтоки та притоки у виробничій, інвестиційній та фінансовій діяльності.
12. Амортизаційна політика та її роль у фінансовому забезпеченні інвестицій.
13. Міжнародна інвестиційна діяльність та її інститути.
14. Особливості формування портфеля реальних інвестиційних проектів.
15. Оцінка альтернативних, конкуруючих і споріднених інвестицій.
16. Індикатори фондового ринку. Світові та українські фондові індекси.
17. Оцінка портфеля цінних паперів за критеріями доходності, ризику та ліквідності.
18. Кредитно-грошові методи регулювання інвестиційних процесів та їх характеристика, механізм дії.
19. Значення антимонопольних заходів при створенні умов для стимулювання інвестиційної діяльності та залучення інвестицій.
20. Політика держави по залученню іноземних інвестицій.
|
|
|
Навчальні завдання для практичних занять
Практичне заняття №1 (2 год.) на тему
«Методологічні системи інвестиційного менеджменту»
План заняття:
І. Обговорення лекційного матеріалу:
1. Види інвестицій.
2. Сутність інвестиційної діяльності.
3. Зміст та функції інвестиційного менеджменту.
4. Інвестиційне планування, організація, контроль.
5. Інформаційне забезпечення інвестиційного менеджменту.
ІІ. Розв’язання ситуаційного завдання
Побудувати організаційні структури з центрами управління інвестиційною діяльністю:
· для малих за розміром підприємств;
· для середніх підприємств;
· для великих підприємств із широко диверсифікованою виробничою чи регіональною діяльністю;
· для дуже великих підприємств.
Підприємства обираються студентом самостійно.
ІІІ. Підведення підсумків заняття.
Практичне заняття №2 (2 год.) на тему
«Методичний інструментарій інвестиційного менеджменту»
План заняття:
І. Вивчення методичного інструментарію оцінювання вартості грошей в часі.
ІІ. Розв’язання аналітичних завдань.
ІІІ. Підведення підсумків заняття.
|
|
|
1. Методичний інструментарій оцінювання вартості грошей за простими відсотками
1.1. Для розрахунків суми простого відсотка в процесі зростання вартості (компаундінга) використовується формула
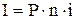, (1)
де I – сума відсотка за обумовлений період часу в цілому; P – початкова сума (вартість) грошей; n – кількість інтервалів, за якими виконується розрахунок відсоткових платежів; i – ставка відсотка, що використовується.
У цьому випадкові майбутня вартість вкладу з урахуванням суми відсотка визначається за формулою
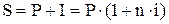. (2)
Приклад 1. Необхідно визначити суму простого відсотка за рік при наступних вихідних даних: початкова сума вкладу P = 1000 у.о.; відсоткова ставка, що виплачується щоквартально, i = 20% = 0,2;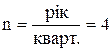 
.
Розв’язання
1) За формулою (1) отримуємо суму простого відсотка
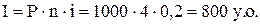
2) За формулою (2) визначаємо майбутню вартість вкладу
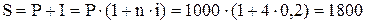у.о.
1.2. Для розрахунку суми простого відсотка у процесі дисконтування вартості (тобто суми дисконту) використовується формула
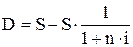, (3)
де D – сума дисконту ( що розрахована за простими відсотками) за обумовлений період часу в цілому; S – вартість коштів; n, i – див. формулу (1).
|
|
|
Тоді поточна вартість грошей (Р) (або первісна їх вартість) з урахуванням суми дисконту визначається за формулою
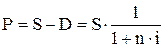. (4)
Приклад 2. Необхідно розрахувати суму дисконту за простим відсотком за рік при таких вихідних даних: кінцева сума вкладу визначена у розмірі
S = 1000 у.о.; дисконтна ставка становить i = 20% = 0,2 у квартал, тобто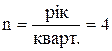 
.
Розв’язання
1) За формулою (3) визначаємо суму дисконту
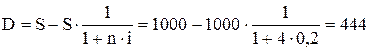у.о.
2) За формулою (4) розраховуємо поточну вартість грошей
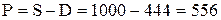у.о.
2. Методичний інструментарій оцінювання вартості грошей за складними відсотками
2.1. Для розрахунку майбутньої суми вкладу (вартості грошей) у процесі його зростання використовується формула
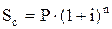, (5)
де Sc – майбутня сума вкладу (грошей) при його зростанні за складними відсотками; P – первинна (початкова) вартість вкладу; i – ставка відсотка, що використовується; n – кількість інтервалів, за якими здійснюються відсоткові платежі.
Відповідно сума відсотка Ic буде
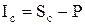. (6)
Приклад 3. Необхідно визначити майбутню вартість вкладу і суму складного відсотка за весь період інвестування за таких вихідних даних: початкова вартість – P= 1000 у.о.; відсоткова ставка, що використовується для розрахунку складного відсотка, визначена у розмірі i = 20% = 0,2 у квартал; загальний термін інвестування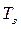 
= 1 рік, тому 
.
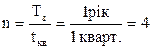Розв’язання
1) За формулою (5) встановлюємо майбутню вартість вкладу
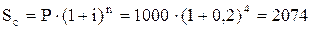у.о.
2) За формулою (6) розраховуємо суму відсотка
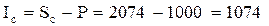у.о.
2.2. Для розрахунку поточної вартості грошей у процесі дисконтування за складними відсотками використовується формула
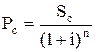, (7)
де Pc– початкова ( поточна) вартість грошей ( сума вкладу); Sc – майбутня вартість вкладу при його зростанні, що обумовлена вимогами інвестування; i – ставка відсотка, що використовується; n – кількість інтервалів, за якими виконуються платежі.
Відповідно сума дисконту Dc буде
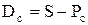. (8)
Приклад 4. Необхідно визначити поточну вартість грошей та суму дисконту за складними відсотками за таких вихідних даних: майбутня вартість грошей – S = 1000 у.о.; ставка складного відсотка для дисконтування, що використовується, – i = 20% = 0,2 у квартал.
Розв’язання
1) За формулою (7) отримуємо поточну вартість
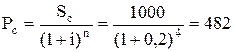у.о.
2) За формулою (8) розраховуємо суму дисконту
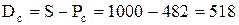у.о.
2.3. Для визначення середньої відсоткової ставки ( icp ) , що використовується при розрахунках вартості грошей за складними відсотками, застосовують формулу
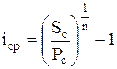, (9)
де Sc– майбутня вартість грошей; Pc – поточна вартість грошей; n – кількість інтервалів, для яких виконується кожний відсотковий платіж.
Приклад 5. Необхідно розрахувати річну ставку дохідності облігацій за наступних умов: номінал облігації, що підлягає погашенню через Tз = 3 роки, становить Sc = 1000 у.о.; вартість, за якою акція реалізується в період її емісії (початкова), складає Pc = 600 у.о.;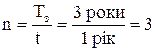 
.
Розв’язання
За формулою (9) визначаємо середньорічну ставку дохідності
.
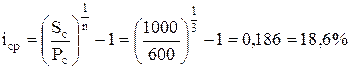2.4. Тривалість загального періоду платежів, що виражена кількістю його інтервалів, при розрахунках вартості коштів (грошей) за складними відсотками розраховується так:
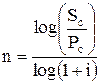, (10)
де Sc і Pc – майбутня і поточна вартість грошей, i – ставка складного відсотка.
2.5. Визначення ефективної відсоткової ставки ( ie ) в процесі зростання вартості грошей за складними відсотками виконується за формулою
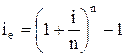, (11)
де ie – ефективна середньорічна відсоткова ставка при зростанні вартості грошей за складними відсотками; i – періодична відсоткова ставка, що використовується при зростанні вартості грошей за складними відсотками; n – кількість інтервалів, за якими виконується кожен відсотковий платіж за періодичними відсотковими ставками протягом року.
Приклад 6. Необхідно визначити ефективну середньорічну відсоткову ставку за наступних умов: грошова сума 1000 у.о. розміщена в комерційному банку на депозитному вкладі терміном на два роки; річна ставка, за якою щоквартально здійснюється нарахування відсотка, дорівнює i = 10% = 0,1.
Розв’язання
За допомогою формули (11) визначаємо
.
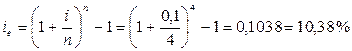Висновок. Результати розрахунків свідчать, що умови розміщення грошей на два роки під 10% річних при щоквартальному нарахуванні відсотків дорівнюють умовам нарахування цих відсотків 1 раз на рік під 10,38% річних (10,38% становить розмір ефективної чи порівняльної відсоткової ставки).
При оцінюванні вартості грошей у часі за складними відсотками необхідно враховувати те, що на результат оцінки дуже впливає не тільки використана ставка відсотка, а й кількість інтервалів виплат протягом одного й того ж загального платіжного періоду. Інколи буває більш доцільно (вигідно) інвестувати кошти під меншу ставку, але з більшою кількістю інтервалів протягом визначеного загального періоду платежів.
Приклад 7. Інвестору треба розмістити 100 у.о. на депозитний вклад терміном на один рік. Один банк пропонує інвестору платити дохід за складними відсотками у розмірі 23% у квартал; другий – 30% кожні 4 місяці; третій – 45% два рази на рік; четвертий – 100% один раз на рік. Необхідно визначити, в якому банку умови розміщення вкладу найкращі.
Розв’язання
Для отримання результату складаємо табл. 1 розрахунків.
Таблиця 1
Дата добавления: 2019-02-12; просмотров: 235; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!