Демпфирование свободных колебаний звеньев
В реальных механизмах относительное движение звеньев всегда сопровождается действием сил сопротивления движению. К ним относят силы трения в кинематических парах, электромагнитного сопротивления в электрических машинах, гидродинамического сопротивления в гидромашинах и т.п. Поэтому колебательные движения звеньев всегда сопровождаются действием сил неупругого сопротивления. Эти силы демпфируют колебания, то есть способствуют их гашению. При определении параметров колебательного процесса величину силы демпфирования в первом приближении принимают пропорциональной скорости движения. Тогда для схемы колебаний на (рис.) закон движения будет описываться дифференциальным уравнением
(G/g)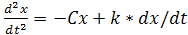 
где k – коэффициент пропорциональности.
Обозначив kg/G = 2n, получим дифференциальное уравнение для свободных колебаний звена с демпфированием
+ 
, (1.32)
решение которого обычно ищут в виде
. (1.33)
Постоянная 
определяется из условия, что решение (1.33)удовлетворяет уравнению(1.32). Определяя из (1.33) 
и подставляя их выражения в уравнение (1.32), получим
(1.34)
Откуда следует, что
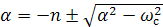. (1.35)
В решении (1.35) при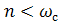 
, что соответствует случаю, когда силы демпфирования достаточно малы, получим два комплексных корня 
(при 
). Подставляя выражения для них в решение (1.33), найдем частные решения. Общее решение получим как сумму частных решений в виде
|
|
|
. (1.36)
Из анализа полученного выражения следует, что при действии демпфирующей силы период колебаний возрастает. При 
это возрастание незначительно и может не учитываться. Множитель 
в зависимости (1.36) убывает с ростом t. Следовательно, колебания при действии демпфирующей силы затухают со временем (1.10). Определяя постоянные в выражении (1.36), получим после преобразования выражение амплитуды колебаний при действии демпфирующей силы
. (1.38)
Если в выражении (1.35) 
> 
, то оба корня уравнения – действительные числа. Тогда получим решение
,
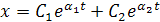которое не содержит периодических членов. Следовательно, при достаточно больших значениях демпфирующих сил колебаний звена нет.
Демпфирование вынужденных колебаний звеньев
В механизмах со сложными кинематическими схемами и сложными конструкциями звеньев трудно выделить источник силы, вызывающей вынужденные колебания. Поэтому в конструктивную схему механизма вводят специальные устройства – демпферы (гасители). С учетом демпфирующих сил для вынужденных колебаний звеньев получим
|
|
|
+ 
q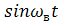 
, (1.39)
где q 
- закон изменения силы, вызывающей вынужденные колебания.
Общим решением дифференциального уравнения (1.39) будет выражение
.
(1.40)
Последние два слагаемых в уравнении (1.40) соответствуют частному решению
(1.41)
для вынужденных колебаний звеньев. Подставляя значения амплитуды для вынужденных колебаний из (1.41) в выражение (1.39), после преобразований найдем
; (1.42)
. (1.43)
После преобразований получим выражение для амплитуды вынужденных колебаний
, (1.44)
где 
– статическая деформация; 
сдвиг фаз собственных и вынужденных колебаний;
1/ 
динамический коэффициент при действии демпфирования (рис.).
Динамический коэффициент при действии демпфирования меняется в широких пределах в зависимости от соотношения частот собственных и вынужденных колебаний. Дифференцируя выражения для 
по (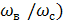 
и приравнивая производную к нулю, получим выражение для максимального значения динамического коэффициента при ( 
.
Дата добавления: 2019-02-12; просмотров: 180; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!