Характеристики вынужденных колебаний звеньев
IX . Колебательные процессы в механизмах.
9 .1 . Виды колебаний звеньев механизмов.
Так как в работающем механизме нагрузки на звенья непрерывно меняются даже при постоянных силах технологического сопротивления, то из-за упругости материалов звеньев они испытывают непрерывно изменяющиеся деформации, вызывающие их колебания. Эти колебания необходимо учитывать при динамических расчетах, так как фактор упругости значительно меняет и системы сил, воздействующих на звенья, и перемещения звеньев. Колебания звеньев в зависимости от их причин разделяют на четыре группы: свободные, вынужденные, параметрические и автоколебания.
К свободным относят колебания, возникающие в механизме
из-за импульсного внешнего силового воздействия. Особенностью свободных колебаний является то, что энергия для возбуждения колебаний вводится в систему извне, а их характер после внешнего воздействия определяется силами упругости. Для свободных колебаний характерно постоянство их амплитуды через определенный период времени Т (рис.1.1, а). При действии силы, способствующей уменьшению амплитуды колебаний с течением времени (рис.1.1,б), колебания затухают.
Колебания, вызванные действием внешних сил, изменяющихся по определенному закону, называют вынужденными, для них характерно протекание одновременно со свободными колебаниями (рис.1.2). Амплитуда вынужденных колебаний меняется во времени, а при определенных условиях имеет тенденцию к неограниченному росту(резонансные колебания).
|
|
|
Параметрические колебания вызываются изменением параметров механизма – масс звеньев, их моментов инерции и др. Например, к параметрическим можно отнести колебания скоростей звеньев из-за изменения приведенных величин. Наконец, автоколебания могут при определенных условиях возникать в машинном агрегате или механизме, под действием сил, которые сами не обладают колебательными свойствами. Режим автоколебаний поддерживается силой, вызываемой движением звеньев и исчезающей при остановке движения. Автоколебаниям подвержены массы грузов, перемещаемые транспортными средствами, детали механизмов и машин и т.п.
Механические колебания с высокой частотой в технике часто называют вибрациями. Вибрации деталей и элементов звеньев оказывают вредное воздействие на работоспособность механизмов, так как вызывают нагружение звеньев дополнительными инерционными усилиями. При больших значениях жесткости звеньев и амплитуд их колебаний эти усилия часто бывают причиной поломок деталей. Есть, однако, машины и механизмы, где вибрации используются как технологический фактор нормального функционирования устройств (вибробункеры, виброконвейеры и т.п.)
|
|
|
Характеристики свободных колебаний звеньев.
Основными характеристиками колебательных систем при известной жесткости являются амплитуда колебаний (обычно представляемая в виде функционального выражения) и период колебаний или их частота. В простейших случаях свободным колебаниям подвержены звенья, совершающие поступательные или вращательные движения: толкатели кулачковых механизмов, разного рода диски и колеса на упругих валах, поршни двигателей и компрессоров и т.д. элементы кинематических пар, образованные этими звеньями, обладают упругостью. Определим выражения для вычисления амплитуд и частот колебаний звеньев, образующих вращательные или поступательные кинематические пары пятого класса.
Пусть звено колеблется после деформирования упругой связи силой тяжести 
(рис.1.3,а). При произвольном положении вертикально перемещающегося звена на него действуют сила тяжести и сила 
, растягивающая пружину
+ 
, (1.1)
где C- жесткость упругой связи; x- перемещение звена от положения равновесия с учетом направления координатной оси. В рассматриваемом положении звено находится в равновесии под действием сил , и силы инерции 
/g)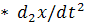 
. Тогда закон движения звена описывается дифференциальным уравнением, справедливым для любого значения координаты x:
|
|
|
/g) 
+ 
, (1.2)
где g – ускорение свободного падения. Далее получим выражение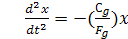 
или 
,
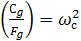(1.3)
Дифференциальному уравнению удовлетворяют частные решения 
и 
, где 
и 
– произвольные постоянные. Общее решение дифференциального уравнения получим как сумму частных решений:
, (1.4)
Так как функции 
и 
являются периодическими, то они повторяют свои значения после некоторого интервала – периода колебаний Т. тогда
, или
, (1.5)
где 
- статическая деформация упругой связи под действием силы . Величина, обратная периоду колебаний Т, называется частотой колебаний:
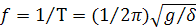. (1.6)
Для определения закона колебательного движения звена необходимо определить постоянные и 
в выражении. При t =0
Положение звена будет характеризоваться перемещением 
. Тогда начальная скорость движения звена будет равна 
. Тогда из выражения(1.4 ) следует, что 
. Дифференцируя выражение и подставляя в производную функцию значение t = 0, получим
|
|
|
. Следовательно, закон колебательного движения звенапри его поступательном движении будет описываться выражением:
. (1.7)
Геометрической интерпретацией выражения (1.7 ) является вектор 
, вращающийся с угловой скоростью 
. Модуль этого вектора равен
. (1.8)
Тогда перемещение или амплитуда колебаний x угла поворота t вектора будут равны
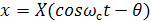, (1.9)
где 
/ 
сдвиг фаз колебаний звена, пропорциональных 
и зависящих от начального перемещения и пропорциональных 
и зависящих от параметра 
.
Во вращательных кинематических парах имеют место крутильные колебания звеньев. При рассмотрении крутильных колебаний звена, обладающего моментом инерции I (рис) после аналогичных рассуждений получим выражения для амплитуды и периода колебаний:
; (1.10)
; (1.11)
. (1.12)
Характеристики вынужденных колебаний звеньев
При действии на звенья периодически изменяющихся внешних сил законы их изменения в реальных механизмах обычно неизвестны или могут быть описаны лишь приближенно. Для определения характеристик вынужденных колебаний звеньев в первом приближении предполагают, что возмущающая сила меняется по периодическому закону 
. Период ее изменения тогда равен 
, а частота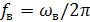 
. Дифференциальное уравнение, описывающее закон вынужденных колебаний звена в этом случае, будет иметь вид
/g) + 
. (1.13)
Обозначив 
, после преобразований приведем выражение к виду 
. (1.14)
Предположим, что амплитуда колебаний 
пропорциональна 
. Тогда получим 
. 
. Подставляя эти значения величин в после преобразований имеем:
. (1.15)
Частное решение дифференциального уравнения(1.14) получим в виде
, (1.16)
а общее решение уравнения при учете собственных и вынужденных колебаний выразим как сумму двух решений:
, (1.17)
В этом выражении первые два слагаемых характеризуют рассмотренные выше собственные колебания звенья, а третье – вынужденные, зависящие от возбуждающей внешней силы. Если собственные колебания малы по сравнению с вынужденными или отсутствуют, что имеет место при сопротивлении движению звеньев, то колебательный процесс будет описываться уравнением. Используя выражения для q и 
, после преобразования получим:
, (1.18)
где 
деформация звена при статическом действии F.
Выражение 
называют динамическим коэффициентом. Динамический коэффициент зависит только от соотношения частот действия возмущающей силы и собственных колебаний. Из графика его изменения (рис.1.4) и выражения видно, что при малых значениях отношения частот вынужденных и собственных колебаний амплитуда колебаний близка к величине статической деформации. При отношениях 
, близких к единице, величина динамического коэффициента и амплитуда колебаний быстро возрастают, и при 
(условие резонанса) величины их значений теоретически обращаются в бесконечность. В реальных механизмах динамический коэффициент 
и амплитуда колебаний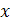 
обычно не достигают больших значений так как на звенья в кинематических парах всегда налагаются и неупругие связи. Однако длительная работа механизмов в зоне резонанса не возможна, т.к. это может привести либо к поломкам деталей, либо к выходу из строя установленных на звеньях приборов и устройств.
Если значения частот и амплитуд собственных и вынужденных колебаний соизмеримы, то функция, описывающая закон колебательного движения, может быть получена из выражения (1.17)после определения значений постоянных 
и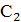 
. При t = 0 имеем: 
, 
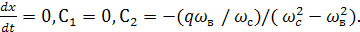Тогда, после преобразований выражения получим (рис 1.5 ):
), (1.19)
При работе механизма в зоне резонансных колебаний его звеньев, когда разность частот 
весьма мала, пренебрегая значениями величин второго порядка малости, получим после преобразования выражения (1.19)
.
Используя известные тригонометрические соотношения, найдем
,
После преобразований, пренебрегая величиной 2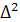 
и считая 
, получим выражение, характеризующее изменение амплитуды колебаний при работе механизма в резонансной зоне частот:
), (1.20)
Так как величина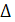 
мала, то значение выражения sin t 
t 
меняется медленно с периодом Т=2π/ . При равенстве частот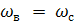 
, то есть при наступлении резонанса, получим
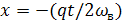
. (1.21)
Анализ этого выражения показывает, что амплитуда растет со временем (рис 1.6). Это означает, что хотя величина динамического коэффициента 
стремится к бесконечности, для достижения опасных для деталей значений амплитуд колебаний необходимо время. Следовательно, в реальном механизме разрушения деталей не наступит, если резонансная зона будет пройдена быстро.
Дата добавления: 2019-02-12; просмотров: 404; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!