Общая характеристика метода статистического моделирования.
Датчики случайных чисел с равномерным распределением.
Каждый раз, когда на ход моделируемого процесса оказывает влияние случайный фактор, его действия имитируются с помощью специально организованного розыгрыша (жребия). Т.о. строится одна случайная реализация моделируемого явления, представляющая собой как бы один результат опыта. По одному опыту конечно нельзя судить о закономерностях изучаемого процесса, но при большом числе реализаций средние характеристики, вырабатываемые моделью, приобретают свойства устойчивости, которые усиливаются с ростом числа реализаций.
Бросание жребия можно осуществить в ручную (выбором из таблицы случайных чисел), однако, удобнее это делать с помощью специальных программ, входящих в состав ПО ЭВМ. Такие программы называют датчиками или генераторами случайных чисел. В трансляторах всех алгоритмических языков имеются стандартные процедуры, которые генерируют случайные стандартные процедуры (псевдослучайные) величины с равномерным распределением.
Моделирование простого события.
Пусть имеется событие А, вероятность наступления которого равна РА. Требуется выработать правила, при многократном использовании которого частота появления событий стремилась бы к его вероятности. Выберем с помощью ДСЧ равномерно распределённых в интервале (0;1) некоторое число z и определим вероятность того, что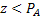 
.
Для случайных величин zравномерно распределённых в интервале (0;1) справедлива следующая зависимость:
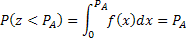
т.о. вероятность того, что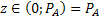 
, поэтому, если при розыгрыше число 
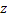попало в этот интервал, то следует считать, что событие А произошло.
Противоположное событие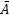 
произойдет с вероятностью 
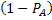в том случае, если 
.
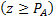Моделирование полной группы несовместных событий и дискретной случайной величины.
Моделирование полной группы несовместных событий.
Пусть имеется полная группа несовместных событий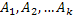 
с вероятностями 
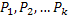. При этомвыполняется условие:
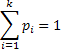
Разделим интервал (0;1) на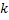 
отрезков, длины которых составляют 
.
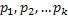Если случайное число Z генерированное датчиком случайных чисел с равномерным распределением в интервале (0;1) попала, например, на участок 
, то это должно означать, что произошло событий 
. Действительно, если обозначить:
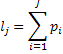
то окажется справедливым выражение:
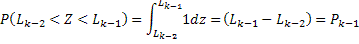
Следовательно, произойдет событие, которое имеет вероятность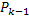 
.
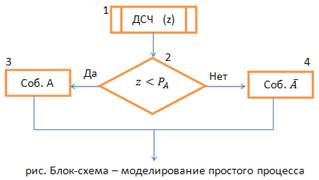
Процедура моделирования полной группы несовместных событий описывается алгоритмом, блок-схема которого имеет вид:
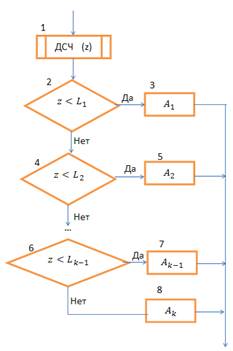
Оператор 1 обращается к ДСЧ с равномерным распределением в интервале (0;1). Условный оператор 2 проверяет условия попадания случайной величины Z в интервал (0;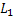 
). Если это условие выполняется, то считается что произошло событие 
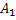. Если условия в операторе 2 не выполняются, то алгоритм осуществляет проверку условия попадания СВ в другие интервалы. Одно из событий 
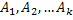обязательно произойдет.
Моделирование дискретной СВ.
Дискретная СВ может быть задана табличной зависимостью:
| X |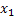 
| 
| … | 
| … | 
|
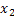
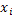
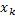
| P |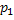 
| 
| … | 
| … | 
|
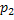
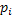
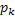
Здесь 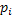вероятность того, что СВ Х принадлежит знач. .
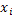при этом по прежнему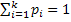 
.
Разделим интервал (0;1) на 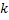отрезков, длины которых равны заданным вероятностям. Если случайное число Z, вырабатываемое ДСЧ попадет в интервал 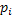, то СВX примет значение 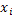. Т.о. моделирование дискретных СВ фактически использует ту же процедуру, что и моделирование полной группы несовместных событий.
Дата добавления: 2019-02-12; просмотров: 192; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!