Системы вытяжки костей при переломах
При сращивании сломанных костей необходимо фиксировать поврежденные участки и устранить силы, которые обычно действуют в месте перелома, до тех пор, пока он не срастется. Для этого используют различные комбинации грузов и блоков.
На рис. 7.25, а показана система вытяжки с использованием двух одинаковых грузов и двух блоков. В этом случае силы натяжения Т1 и Т2 равны. Те же условия можно создать и другим способом (рис. 7.25, б), используя один груз и комбинацию из подвижного и неподвижного блоков. В этом случае общая сила, действующая на ногу, равна векторной сумме двух сил натяжения (рис. 7.25, в).
Рис. 7.25. Два способа вытяжки: а) два груза и два блока, б) один груз и два блока, в) результирующая сила (F)
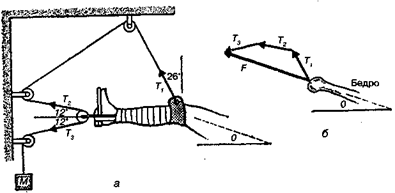
Рис. 7.26. Система вытяжки Рассела
На рис. 7.26, а показана система вытяжки Рассела, применяемая для фиксации сломанного бедра. Эта система получена добавлением к системе, изображенной на рис. 7.25, еще двух блоков для обеспечения связи с коленом. Бедро устанавливается под углом θ = 20° к горизонтали. Остальные углы указаны на рисунке. При этом векторная сумма трех сил натяжения, обозначенная на рис. 7.26, б, F , имеет оптимальное направление.
Глава 8 НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА
Сила инерции. Принцип Д'Аламбера
В ряде случаев возникает необходимость описать движение, покой или равновесие тела, находящегося в неинерциальной системе отсчета. Например, требуется выяснить какие проблемы могут возникнуть у человека, находящегося в кабине космического корабля. Французский физик Д'Аламбер сформулировал простой принцип, позволяющий отвечать на вопросы о поведении тела в неинерциальной системе. Рассмотрим тело, которое находится в неинерциальной системе, движущейся относительно инерциальной системы с ускорением ас.
|
|
|
Векторная величина, равная произведению массы тела на ускорение системы и направленная в сторону, противоположную ускорению системы, называется силой инерции:
F и =-m·ac. (8.1)
Сила инерции не является реальной силой, так как она не действует со стороны какого либо тела. Однако в неинерциальной системе ее можно (и нужно!) рассматривать, как обычную силу. При этом можно «забыть» о том, что система неинерциальна.
Д'Аламбер установил, что если ко всем реальным силам (действующим со стороны других тел) добавить силу инерции, то в неинерциальной системе можно использовать все законы и формулы, которые справедливы для инерциальных систем.
Пример
Пусть тело массой т подвешено на нити в кабине космического корабля, который стартует с Земли и поднимается вверх с ускорением «а».
Система отсчета, связанная с таким кораблем является неинерционной и к ней применим принцип Д'Аламбера (ускорение системы — это ускорение корабля: ас = а). На тело действуют сила тяжести со стороны земли ( mg ) и сила натяжения нити (Т) (рис. 8.1). Добавим к ним силу инерции F и = т · а, которая направлена вниз (в сторону, обратную ускорению). Теперь можно описать покой тела относительно корабля: Т + mg + F и = 0. Учитывая направления сил, получим уравнение для их величин: Т — mg — F и = 0. Откуда найдем натяжение нити, удерживающей тело:
|
|
|
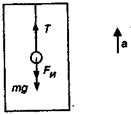
Рис. 8.1. Использование силы инерции
Установлено, что сила инерции неотличима от силы гравитации (силы тяготения). В рассматриваемом примере это означает, что никакие опыты, поставленные внутри корабля, не смогут дать ответ на вопрос, какая из ситуаций имеет место:
• либо мы находимся не в корабле, а на какой-то планете, где ускорение свободного падения равно g + a ;
• либо мы движемся с ускорением g + а на космическом корабле вдали от каких-либо планет (гравитационные силы отсутствуют);
• либо мы стартуем с Земли, поднимаясь с ускорением «а». Во всех этих случаях результаты любого опыта будут совершенно одинаковы.
Сила тяжести.Вес тела
Сила тяжести
Так как сила тяготения и сила инерции неотличимы, то при использовании неинерциальной системы их обычно складывают (как вектора) и эту сумму называют силой тяжести.
|
|
|
Силой тяжести, действующей на тело в неинерциальной системе отсчета, называется сумма силы тяготения и силы инерции:
F тяж =F тяг + F и (8.2)
В рассмотренном выше примере со стартующим кораблем (рис. 8.1) сила тяжести равна:
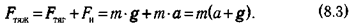
Сила тяжести сообщает всем телам одинаковое ускорение (относительно данной системы), которое называют местным ускорением свободного падения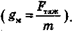 
В примере со стартующим кораблем
gm = a + g .
Обратим внимание на то, что сила тяжести зависит от того, какой системой отсчета мы пользуемся. Так, например, в рассматриваемом случае можно поступить одним из двух способов.
1. Выбрать систему, связанную с Землей. В этой системе тело движется с ускорением под действием силы натяжения нити (Т) и силы тяжести ( mg ). Уравнение движения:
Т - mg = та.
2. Выбрать систему, связанную с кораблем. В этой системе тело находится в состоянии покоя под действием силы натяжения нити (Т) и местной силы тяжести ( mg + та). Уравнение покоя:
T = mg + ma .
Очевидно, что эти уравнения одинаковы.
Для человека, находящегося в корабле, естественным является второй способ. Поэтому он скажет, что при старте сила тяжести возрастает.
|
|
|
С направлением силы тяжести неразрывно связаны такие понятия, как вертикаль и горизонталь.
Вертикалью называется линия, вдоль которой направлена сила тяжести.
Горизонтальной плоскостью называется плоскость, которая перпендикулярна силе тяжести.
Формула (8.2) определяет силу тяжести в любой неинерциальной системе отсчета. Применим ее к Земле, неинерциальность которой связана с вращением вокруг своей оси. Вследствие этого точки земной поверхности обладают центростремительным ускорением (ац), которое и является ускорением неинерциальной системы (ас = ац). По формуле (8.2) находим силу инерции:
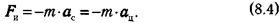
Знак «—» указывает на то, что сила инерции направлена от оси вращения Земли.
Сила тяготения направлена к центру Земли. Складывая эти силы, находим силу тяжести (рис. 8.2).
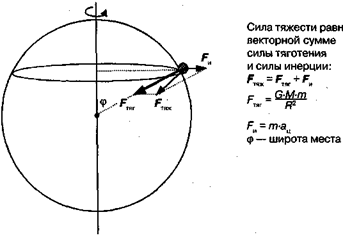
Рис. 8.2. Сила тяготения и сила тяжести
На рис. 8.2 видно отличие силы тяжести от силы тяготения. Наибольшей величины это отличие достигает на экваторе, где сила тяготения и сила инерции направлены по одной прямой в противоположные стороны. При сложении таких векторов (8.2) их величины вычитаются:
Таким образом, сила тяжести отличается от силы тяготения на величину силы инерции. Велико ли это отличие? Для ответа на этот вопрос найдем отношение силы инерции к силе тяжести. Сила тяжести создает ускорение свободного падения: Ргяж = m - g ( g = 9,8 м/с2). Сила инерции вычисляется по формуле (8.3) F = т-а , деля величины этих сил, найдем
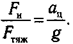(8.6)
Центростремительное ускорение рассчитывается по формуле (3.9):
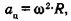
где R — радиус обращения тела, а 0) — угловая скорость вращения Земли. Для экватора R = 6 400 000 м — радиус Земли. Угловая скорость выражается через период обращения (Т), который для Земли составляет 1 сутки или 86400 с. В соответствии с формулой (3.10) ω=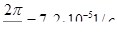 
. Центростремительное ускорение на экваторе ац= ω 2R 
0,03 м/с2. Подставив это значение в (8.5) получим
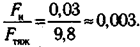
Из приведенных расчетов видно, что для Земли сила инерции составляет всего 0,3% от силы тяжести. Поэтому в большинстве случаев неинерциальностью Земли можно пренебречь.
Вес тела
Рассмотрим, что происходит, когда некоторый груз кладут на горизонтальную плоскость (опору). В первый момент после того, как груз отпустили, он начинает двигаться вниз под действием силы тяжести (рис. 8.3). Плоскость прогибается и возникает сила упругости (реакция опоры), направленная вверх. После того, как сила упругости ( F ) уравновесит силу тяжести, опускание тела и прогиб опоры прекратятся.
Прогиб опоры возник под действием тела, следовательно, со стороны тела на опору действует некоторая сила (Р), которую называют весом тела (рис. 8.3, б). По третьему закону Ньютона вес тела равен по величине силе реакции опоры и направлен в противоположную сторону.
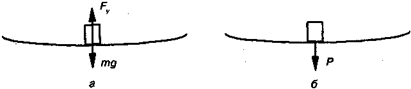
Рис. 8.3. Силы, действующие на тело (а) и опору (б) тела равен по величине силе реакции опоры и направлен в противоположную сторону.
Вместо опоры можно использовать подвес.
Весом теланазывают силу Р, с которой тело действует на неподвижную относительно него горизонтальную опору (или неподвижный относительно него подвес).
Вес не следует путать с массой тела. Масса тела характеризует его инертные свойства и не зависит ни от силы тяготения, ни от ускорения, с которым оно движется. Вес тела характеризует силу, с которой оно действует на опору и зависит как от силы тяготения, так и от ускорения движения. Например, на Луне вес тела примерно в 6 раз меньше, чем вес тела на Земле. Масса же в обоих случаях одинакова и определяется количеством вещества в теле.
Вес тела — понятие скорее инженерное, чем физическое, и используется не часто. Например, при проектировании моста указывают вес, который он должен выдерживать. В быту понятие «вес» используется, как правил о, некорректно, поскольку имеется в виду масса тела. Например, когда говорят о весовых категориях, в спорте, то подразумевают не силу, с которой спортсмен давит на помост, а его массу. В то же время, говоря о весе поднятой штанги, понятие «вес» употребляют совершенно правильно, так как речь идет о силе, с которой штанга действует на человека. Существующая путаница в употреблении понятия «вес» не влечет никаких отрицательных последствий, так как в каждой области люди интуитивно понимают, что имеется в виду.
В быту, технике, спорте вес часто указывают не в ньютонах (Н), а в килограммах силы (кгс). Переход от одной единицы к другой осуществляется по формуле
1кгс = 9,8Н.
Дата добавления: 2019-01-14; просмотров: 323; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!