Основные понятия и определения
Игра- упрощенная модель конфликта для решения конфликтных ситуаций. Разработан специальный аппарат - теория игр. Стороны, участвующие в конфликте называются игроками.
Для задания правил необходимо определить:
1)Варианты действия игроков;
2)Объем информации каждого игрока о поведении противника;
3) Выигрыш, к которому приводит совокупность действий игроков;
Если в игре принимают участие два игрока, то игра называется парной. Если же количество игроков больше двух, то игра называется множественной.
Игра, в которой выигрыш одного из игроков равен проигрышу другого, называется игрой с нулевой суммой (антагонистической игрой).
Совокупность правил, определяющих выбор действий игрока в зависимости от сложившейся ситуации, называется стратегией.
Решить антагонистическую задачу (игру) значит для каждого игрока указать стратегию, удовлетворяющую условию оптимальности, то есть игрок А должен получить максимальный выигрыш, а игрок В должен получить минимальный проигрыш.
Оптимальные стратегии характеризуются устойчивостью, то есть не одному из игроков не выгодно отклоняться от своей оптимальной стратегии. В игре с полной информацией перед каждым ходом игрок знает все предшествующие ходы и выигрыши. В кооперативных играх допускается возможность предварительных переговоров между игроками.
Предположим, что для пары стратегий А i и Bj выигрыш известен – ν ij, тогда можно составить прямоугольную таблицу (матрицу), в которой показаны все стратегии игроков и соответствующие выигрыши. Такая матрица называется платежной.
|
|
|
| B1 | B2 | |
| А1 | 5 | -4 |
| А2 | 4 | 3 |
| А3 | 2 | 1 |
Положительные числа в клетках матрицы означают выигрыш игрока А и следовательно проигрыш игрока В. Отрицательное число означает проигрыш игрока А и следовательно выигрыш игрока В.
Решение игры с седловой точкой
| B1 | B 2 | |
| А1 | 5 | -4 |
| А2 | 4 | 3 |
| А3 | 2 | 1 |
Рассмотрим подробнее игровую матрицу. У игрока А имеется 3 стратегии, а у игрока В – 2 стратегии. Нужно определить какую стратегию нужно выбрать игроку А, чтобы его выигрыш был максимальным, проигрыш игрока В был бы минимальным.
| B 1 | B2 | min | |
| А1 | 5 | -4 | -4 |
| А2 | 4 | 3 | 3 |
| А3 | 2 | 1 | 1 |
| max | 5 | 3 |
Для этого введем несколько понятий:
Нижняя цена игры: Сначала находим минимумы в каждой строке, заносим их в таблицу.
Из полученных минимумов находим максимум: α=maxmin ν ij;
α=3 – это гарантированный выигрыш игрока А при любой стратегии игрока В.
Верхняя цена игры: Сначала находим максимум в каждом столбце, определяем минимальное число: β=minmax νij;
β=3 – гарантированный проигрыш игрока В при любой стратегии игрока А.
|
|
|
Если α=β=ν, то в этом случае выбранные стратегии называются оптимальными, а саму игру называют игрой с седловой точкой. В этом случае у игрока А стратегия А2 и у игрока В стратегия В2. При выборе других стратегий выигрыш игрока А будет меньше, а проигрыш игрока В больше.
Задача
Найти седловую точку матрицы:
| B 1 | B2 | B3 | min | |
| А1 | 1 | 2 | 1 | -1 |
| А2 | 3 | -5 | -1 | 5 |
| А3 | -1 | 7 | -2 | -2 |
| max | 3 | 7 | 1 |
α =1;
β = 1; cедловая точка А1;В3, а выигрыши ν1А=ν3В=1.
Однако, на практике чаще встречаются случаи когда платежная матрица не имеет седловой точки. Такие задачи называются задачами со смешанными стратегиями.
Смешанные стратегии
Рассмотрим пример
| B 1 | B2 | min | |
| А1 | 5 | 8 | 5 |
| А2 | 6 | 4 | 4 |
| max | 6 | 8 |
α=5; β=6; α≠β;
В этой задаче нет седловой точки и игроки должны применять смешанные стратегии. Для нахождения смешанных стратегий используется несколько методов:
1) Определение цены игры методом подбрасывания монеты;
2) Определение относительных частот применения смешанных стратегий;
3) Использование частот и вероятностей, полученных при многократной игре;
Определение цены игры методом подбрасывания монеты
|
|
|
| B 1 | B2 | min | |
| А1 | 5 | 8 | 5 |
| А2 | 6 | 4 | 4 |
| max | 6 | 8 |
Пусть смешанная стратегия игрока А определяется подбрасыванием монеты:
А1 – «орел», А2 – «решка».
Средний выигрыш игрока А против первой стратегии игрока В:
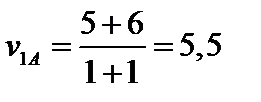
а против второй:
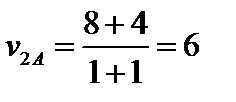
В обоих случаях результат для игрока А будет лучше, чем при выборе любой стратегии. Цена игры всегда лежит в пределах: 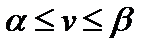 .
.
Определение относительных частот применения смешанных стратегий
| B 1 | B2 | ||
| А1 | 5 | 8 | 3 |
| А2 | 6 | 4 | 2 |
| 1 | 4 |
Если игра не имеет седловой точки, то наилучшей будет смешанная стратегия. Для нахождения оптимальной стратегии нужно выполнить следующее:
a) Рассмотрим стратегии игрока В. Из первой строки вычитаем числа второй, тогда частоту применения первой стратегии примем равной 4, а частоту второй стратегии 1, то есть стратегии игроком В1 и В2 должны применятся в отношении 4:1.
Отметим, что если число, характеризующее относительную частоту окажется отрицательным, то на знак не обращают внимания.
б) Аналогичным образом определяются частоты применения стратегий игрока А и они относятся как 2:3.
в) Найдем цену игры при применении против первой стратегии игрока В. Она будет равна:
|
|
|

А цена игры против второй стратеги равна:

Можно убедиться, что средний выигрыш игрока А в данном случае больше, чем при применении любых других стратегий.
Использование вероятностей применения стратегий для получения цены смешанных стратегий
В случае если нижняя цена игры не равна верхней, то седловой точки нет. В этом случае для каждого игрока нужно указать вектор частот, с которыми нужно применять ту или иную стратегию.
Для игрока А: Р=(р1…р m), где р1 +…+ р m =1.
Pi ≥0 – частота применения стратегии А i.
Для игрока В: Q =(q 1 … qn), где q 1 +…+ qn =1.
qj ≥0 – частота применения стратегии В j.
В этом случае ν(P 0 Q 0 ) называют ценой игры и обозначают через ν и 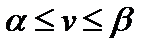 .
.
Пример
Рассмотрим решение игры (смотри таблицу).
| q | 1-q | |||
| B 1 | B2 | 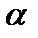
| ||
| p | А1 | - 5 | 8 | -5 |
| 1-p | А2 | 4 | -7 | -7 |
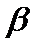
| 4 | 8 |
В данном примере седловая точка отсутствует, тогда оптимальная цена игры -5≤ ν ≤4.
Припишем строкам вероятности р и 1-р.
Умножив столбец 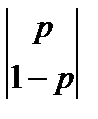 поэлементно на первый столбец и сложив произведения получим линейную зависимость:
поэлементно на первый столбец и сложив произведения получим линейную зависимость:
W ( p )=-5 p +4(1- p )=-9 p +4 (1)
(1) – это средний выигрыш игрока А при применении игроком В первой стратегии.
Умножив столбец 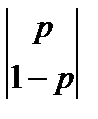 поэлементно на второй столбец и сложив произведения получим:
поэлементно на второй столбец и сложив произведения получим:
W ( p )=8 p +(-7)(1- p )=15 p -7 (2)
(2) – это средний выигрыш игрока А при применении игроком В второй стратегии.
Приравняем (1) и (2)
-9 p +4=15 p -7
Отсюда 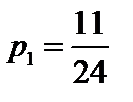 ;
; 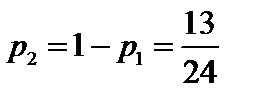 .
.
Таким образом оптимальная смешанная стратегия игрока А - это 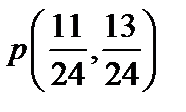 , т.е. игрок А должен применять первую стратегию игрока В с частотой
, т.е. игрок А должен применять первую стратегию игрока В с частотой 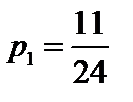 и вторую стратегию игрока В с частотой
и вторую стратегию игрока В с частотой 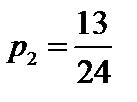 .
.
Подставив в зависимости (1) и (2) соответственно p 1 и p 2 получим цену игры
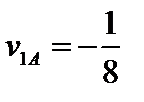 ;
; 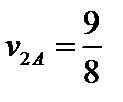 (3)
(3)
Теперь припишем столбцам вероятности q и 1- q. Умножив строку (q ,1- q) на первую строку и сложив произведения, получим
W ( q )=(- 5) q +8(1- q )=-13 q +8 (4)
(4) – средний выигрыш игрока В при применении игроком А первой стратегии.
Аналогично со второй строкой
W ( q )=4 q +(-7)(1- q )=11 q -7 (5)
(5) – средний выигрыш игрока В при применении игроком А второй стратегии.
Приравнивая зависимости (4) и (5) получим:
-13 q +8=11 q -7
Отсюда 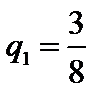 ;
; 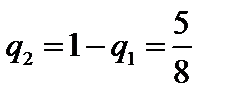 , т.е. оптимальная смешанная стратегия игрока В – это
, т.е. оптимальная смешанная стратегия игрока В – это 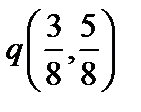 . Подставив в зависимости (4), (5) соответственно q 1 и q 2, получим цену игры игрока В.
. Подставив в зависимости (4), (5) соответственно q 1 и q 2, получим цену игры игрока В.
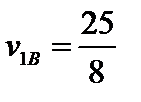 ;
; 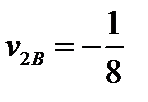 (6)
(6)
Сравнивая (3) и (6) находим, что 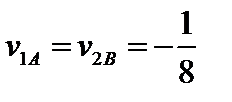 – это и есть оптимальная цена игры, которая возможна при оптимальной смешанной стратегии
– это и есть оптимальная цена игры, которая возможна при оптимальной смешанной стратегии 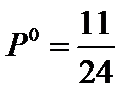 и
и 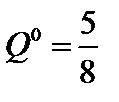 .
.
Таким образом, оптимальная цена игры 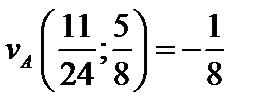 и действительно
и действительно 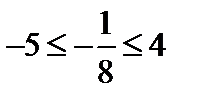 .
.
4. Решение игры 2 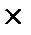 n
n
Самым удобным способом для определения оптимальной стратегии игроков в игре 2 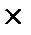 n является графическим способом.
n является графическим способом.
Пример
| B 1 | B2 | B 3 | B 4 | |
| А1 | -1 | 1 | -1 | 2 |
| А2 | 0 | -1 | 2 | -2 |
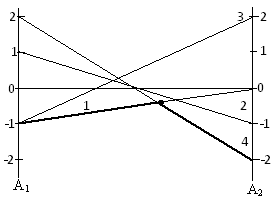
Отложим на двух вертикальных осях платежи сначала первой стратегии В1(-1,0) и соединим их линией, а затем остальные стратегии игрока В. Отметим утолщенной линией нижнюю границу графика. Затем найдем наивысшую точку этой линии. Линии пересекающиеся в этой точке соответствуют тем чистым стратегиям, которые должен применить игрок В в своей смешанной стратегии. На графике в этой точке пересекаются линии, соответствующие стратегиям В1 и В4. Таким образом остается матрица по первой и четвертой стратегиям игрока В:
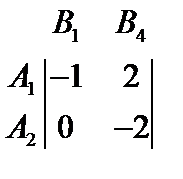
Решим методом определения относительных частот применения смешанных стратегий. Получим:
- игрок А должен применить стратегии А1 и А2 в отношении 2:3, тогда цена игры:
| B 1 | B2 | ||
| А1 | -1 | 2 | 3 |
| А2 | 0 | -2 | 2 |
| 1 | 4 |
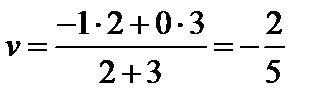
- игрок В должен применять стратегии В1 и В4 в отношении 4:1, тогда
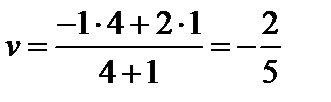
Т.о. оптимальная цена игры 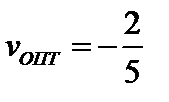 .
.
5. Решение игры m  2
2
Используя метод вероятностей применения стратегий, решить игру 3  2.
2.
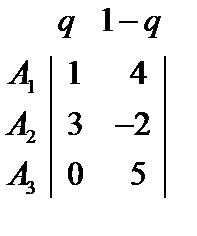
Припишем вероятности столбцов для q; 1- q, в результате получим линейные зависимости
W ( q )=1 q +4(1- q )=4-3 q (1)
W ( q )=3 q +(-2)(1- q )=5 q –2 (2)
W ( q )=0· q +5(1- q )=5-5 q (3)
Изобразим данные линейные зависимости графически:
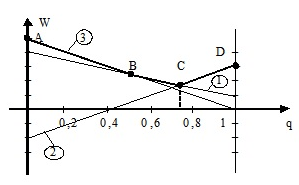
Возьмем верхнюю огибающую. Точка С – точка с наименьшим выигрышем (W), точка пересечения прямых (1) и (2). Приравняем первую и вторую зависимости и определим вероятности:
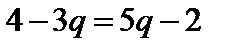 ;
; 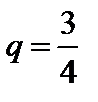
Цена игры в этом случае:

При корректном построении можно легко определить вероятность применения смешенных стратегий и цену игры.
Примеры решения задач
Задача 1
Найти решение игры, определяемой матрицей
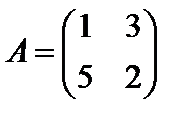
Решение:
Данная игра седловой точки не имеет: α=2, β=3.
Поэтому ищем решение в смешанных стратегиях:
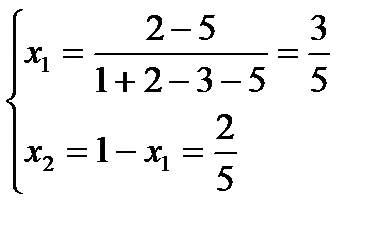
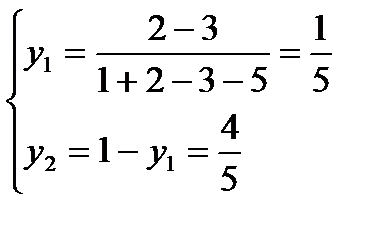
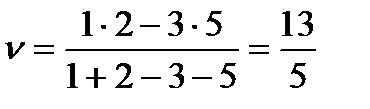
Ответ: общее решение имеет вид:
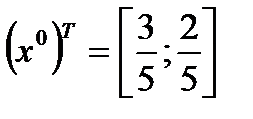 ;
; 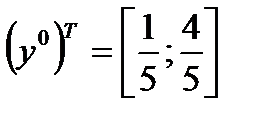 ;
; 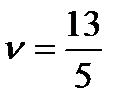 .
.
Задача 2
Найти решение игры 2 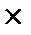 2 с использованием понятия равновесия по Нэшу
2 с использованием понятия равновесия по Нэшу
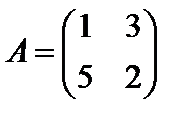
Решение:
Определим по формуле 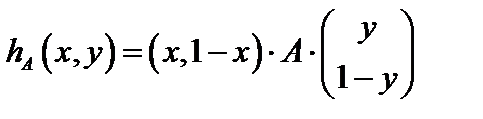 математическое ожидание выигрыша игрока А:
математическое ожидание выигрыша игрока А:
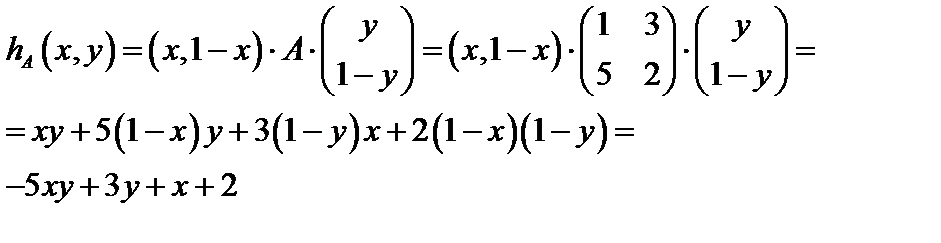
Определим точку Нэша
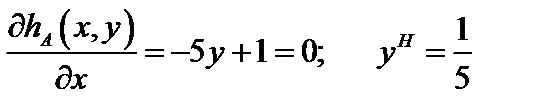
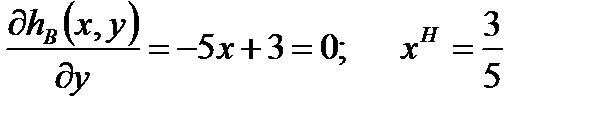
(xH, yH) – координаты точки равновесия по Нэшу.
Таким образом, оптимальные стратегии в данной игре следующие
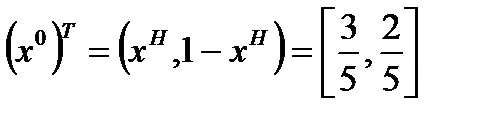 ;
; 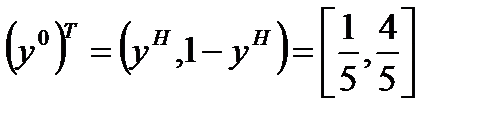
Цена игры в точке Нэша
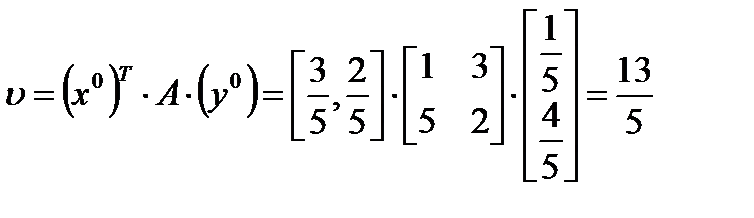
Ответ: общее решение имеет вид:
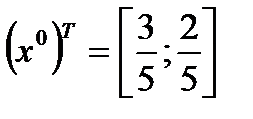 ;
; 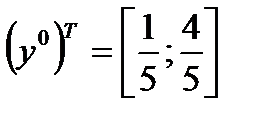 ;
; 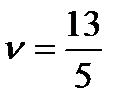 .
.
Примеры заданий
Вариант 0
Зная платежную матрицу

определить нижнюю и верхнюю цены игры и найти решение игры.
Вариант 1
Игра задана платежной матрицей. Определить седловую точку.

Вариант 2
Игра задана платежной матрицей. Определить седловую точку.
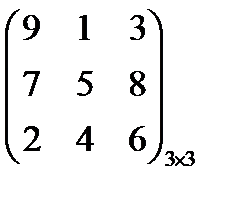
Вариант 3
Игра задана платежной матрицей. Определить верхнюю цену игры.
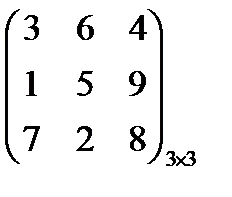
Вариант 4
Игра задана платежной матрицей. Определить нижнюю цену игры.
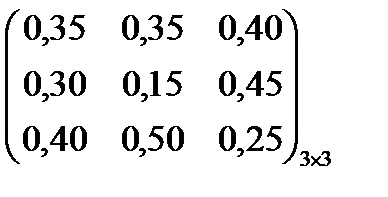
Вариант 5
Игра задана платежной матрицей. Определить нижнюю верхнюю цены игры.
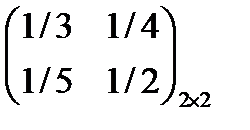
Вариант 8
Игра задана платежной матрицей. Определить седловую точку.
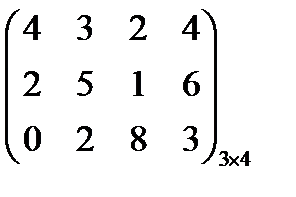
Вариант 9
Игра задана платежной матрицей. Определить вероятности P1 и P2 применения стратегий А1 и А2 для оптимальной смешанной стратегии игрока А.
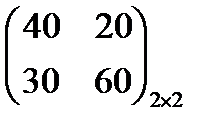
Вариант 10
Игра задана платежной матрицей. Определить вероятности q1 и q2 применения стратегий В1 и В2 для оптимальной смешанной стратегии игрока В.
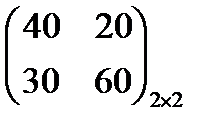
Вариант 11
Игра задана платежной матрицей. Определить цену игры, если вероятности P1 и P2 применения стратегий А1 и А2 для оптимальной смешанной стратегии игрока A равны 0,6 и 0,4.
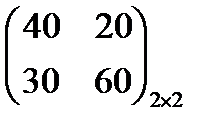
Вариант 12
Найти графически стратегии игроков А, В и цену игры, заданной матрицей.
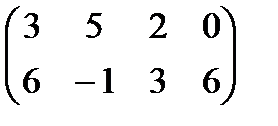
Вариант13
Найти графически стратегии игроков А, В и цену игры, заданной матрицей.
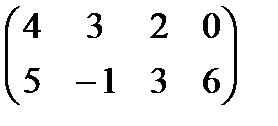
Вариант 14
Найти графически стратегии игроков А, В и цену игры, заданной матрицей.
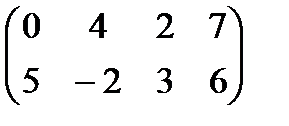
Вариант 15
Найти графически стратегии игроков А, В и цену игры, заданной матрицей.
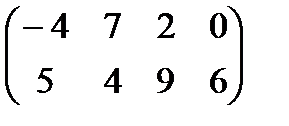
ПОДГОТОВКА КУРСОВОЙ РАБОТЫ
Темы курсовых работ
Дата добавления: 2019-01-14; просмотров: 243; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
