Задача о застройке микрорайона
Министерство образования и науки Российской Федерации
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра прикладной математики
ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Методические указания к практическим занятиям
и подготовке курсовой работы
(Издание в качестве методических указаний)
Составители Б.П.Титаренко, Ю.Г.Жеглова
© Национальный исследовательский
Московский государственный
строительный университет, 2018
УДК 519.6
ББК 22.176
Д 48
Рецензент –кандидат физ.-мат. наук, профессор кафедры прикладной математики НИУ МГСУ Ю.В.Осипов
Д 48 Исследование операций . [Электронный ресурс]Методические указания к практическим занятиям и подготовке курсовой работы для обучающихся по направлениям подготовки 01.03.04 Прикладная математика , 09.03.01 Информатика и вычислительная техника, 09.03.02 Информационные системы и технологии (Издание в качестве методического пособия) / сост. Б.П.Титаренко, Ю.Г. Жеглова; М-во образования и науки Рос. Федерации, Нац. исследоват. Мос. гос. строит. ун-т; каф. прикл. мат-ки ( Мб) – Москва; Из-во Моск. гос. строит. ун-та, 2018. Режим доступа –
Методические указания предназначены для студентов, изучающих дисциплину « Исследование операций». Приведены варианты заданий, примеры решения задач , темы курсовых работ и требования к подготовке курсовой работы
|
|
|
Учебное электронное издание
© Национальный исследовательский
Московский государственный
строительный университет, 2018
ОГЛАВЛЕНИЕ
1. ЭЛЕМЕНТЫ ТЕОРИИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ……4
2. ТРАНСПОРТНАЯ ЗАДАЧА……………………………………………….16
3. ЭЛЕМЕНТЫ ТЕОРИИ ИГР……………………………………………….29
4. ПОДГОТОВКА КУРСОВОЙ РАБОТЫ………………………………….43
БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………………………47
1. ЭЛЕМЕНТЫ ТЕОРИИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
В настоящее время множество задач планирования и управления в отраслях народного хозяйства, а также большой объём частных прикладных задач решаются методами математического программирования. Наиболее развитыми в области решения оптимизационных задач являются методы линейного программирования. Эти методы позволяют описать с достаточной точностью широкого круга задач коммерческой деятельности, таких, как планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров; распределение работников торговли должностям; организация рациональных закупок продуктов питания; распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.
|
|
|
Линейное программирование – это направление математического программирование, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейной целевой функцией. Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения.
Основная задача линейного программирования (ОЗЛП)
Найти экстремум (max или min) линейной функции
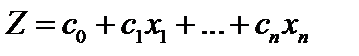
при линейных ограничениях
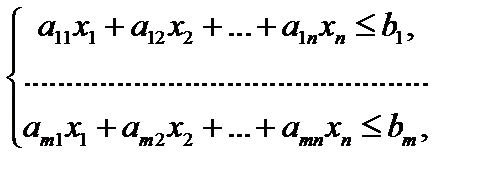
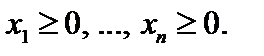
Двумерные задачи линейного программирования решаются графически. Для случая n =3 можно рассмотреть трехмерное пространство и целевая функция будет достигать своё оптимальное значение в одной из вершин многогранника.
В общем виде, когда в задаче участвуют n-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
|
|
|
Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные X 1, X 2, ..., Xr. Тогда наша система уравнений может быть записана как
|
|
|
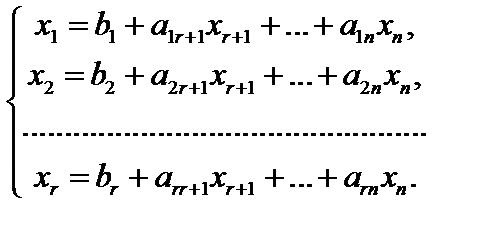
К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.
Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные X 1, X 2, ..., Xr, то решение {b1, b2 ,..., br, 0, ..., 0} будет опорным при условии, что b1, b2, ..., br ≥ 0.
Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.
Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.
Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.
Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.
Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.
Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.
Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.
Приведенная схема симплексного метода явно выражает его алгоритмический характер (характер четкого предписания о выполнении последовательных операций), что позволяет успешно программировать и реализовать этот метод на ЭВМ. Задачи же с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.
Не останавливаясь подробнее на сути алгоритма, опишем его вычислительную сторону. Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные. Вопрос об этих предварительных преобразованиях мы рассмотрим ниже. Сейчас же будем считать, что они уже выполнены и задача имеет вид:
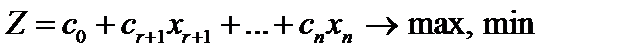
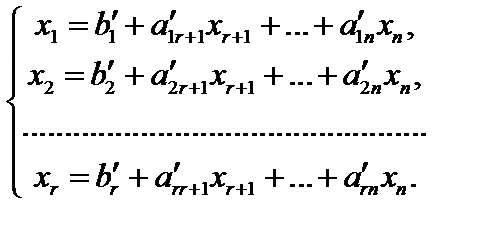
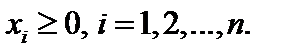
Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные X 1, X 2, ..., Xr и что при этом b1, b2, ..., br ≥ 0 (соответствующее базисное решение является опорным).
Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств:
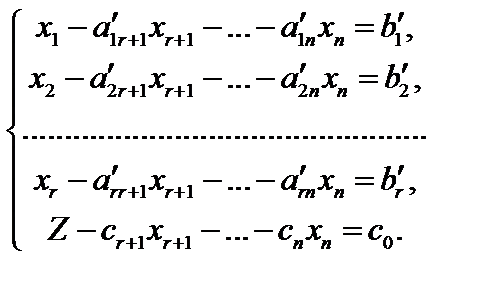
Далее эта система оформляется в виде симплекс-таблиц:
| Баз. перем. | Своб. члены | X 1 | X2 | … | … | Xr | Xr+1 | Xr+2 | … | … | … | Xn |
| X 1 | 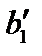
| 1 | 0 | … | … | 0 | 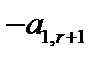
| 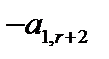
| … | … | … | 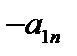
|
| X2 | 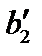
| 0 | 1 | … | … | 0 | 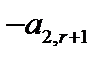
| 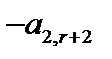
| … | … | … | 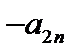
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| Xr | 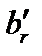
| 0 | 0 | … | … | 1 | 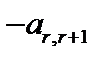
| 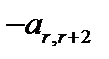
| … | … | … | 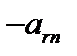
|
| Z | 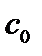
| 0 | 0 | … | … | 0 | 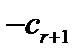
| 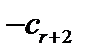
| … | … | … | 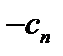
|
Примечание. Названия базисных переменных здесь взяты лишь для определенности записи и в реальной таблице могут оказаться другими.
Порядок работы с симплекс таблицей
Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению.
Алгоритм перехода к следующей таблице такой:
· просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов) выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;
· просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;
· среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находится ключевой;
· в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:
· разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы.
· строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место.
· в новой таблице все элементы ключевого столбца = 0, кроме разрезающего, он всегда равен 1.
· столбец, у которого в ключевой строке имеется 0, в новой таблице будет таким же.
· строка, у которой в ключевом столбце имеется 0, в новой таблице будет такой же.
· в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы:
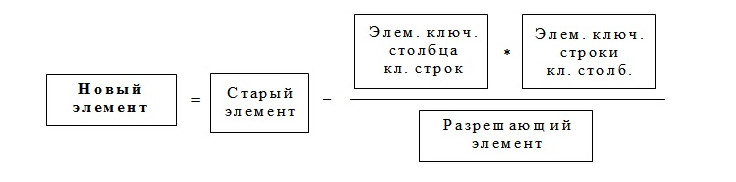
В результате получают новую симплекс-таблицу, отвечающую новому базисному решению.
Теперь следует просмотреть строку целевой функции (индексную), если в ней нет отрицательных значений (в задачи на нахождение максимального значения), либо положительных (в задачи на нахождение минимального значения) кроме стоящего на месте (свободного столбца), то значит, что оптимальное решение получено. В противном случае, переходим к новой симплекс таблице по выше описанному алгоритму.
Пример
ЗАДАНИЕ. Компания производит полки для ванных комнат двух размеров – А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В – 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В – 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В – 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?
РЕШЕНИЕ. Составим математическую модель задачи. Пусть х1 – количество полок вида А, х2 – количество полок вида В, которые производятся в неделю (по смыслу задачи эти переменные неотрицательны). Прибыль от продажи такого количества полок составит 3х1 + 4х2, прибыль требуется максимизировать. Выпишем ограничения задачи.
х1 + х2 ≤ 550 – в неделю на рынке может быть реализовано до 550 полок.
Затраты материала: 2х1 + 3х2 ≤ 1200
Затраты машинного времени: 12х1 + 30х2 ≤ 9600.
Таким образом, приходим к задаче линейного программирования.
f = 3х1 + 4х2 → max,
х1 + х2 ≤ 550,
2х1 + 3х2 ≤ 1200,
12х1 + 30х2 ≤ 9600,
x1≥ 0, x2≥0.
Решим ее симплекс-методом. Введем три дополнительные переменные x3, x4, x5 и придем к задаче
f = 3х1 + 4х2 → max,
х1 + х2 + x3 = 550,
2х1 + 3х2 + x4 = 1200,
12х1 + 30х2 + x5 = 9600,
xi ≥ 0, i=1,2,3,4,5.
В качестве опорного плана выберем X0=(0, 0, 550, 1200, 9600). Составим симплекс-таблицу.
| Базис | План | x1 | x2 | x3 | x4 | x5 |
| x3 | 550 | 1 | 1 | 1 | 0 | 0 |
| x4 | 1200 | 2 | 3 | 0 | 1 | 0 |
| x5 | 9600 | 12 | 30 | 0 | 0 | 1 |
| F | 0 | -3 | -4 | 0 | 0 | 0 |
В последней оценочной строке есть отрицательные оценки, поэтому нужно делать шаг симплекс-метода. Выбираем столбец с наименьшей оценкой, а затем разрешающий элемент – по наименьшему отношению свободных членов к коэффициентам столбца (последний столбец). Результат шага запишем в таблицу (разрешающий элемент будем выделять жирным). Аналогично будем повторять шаги, пока не придем к таблице с неотрицательными оценками.
| Базис | План | x1 | x2 | x3 | x4 | x5 |
| x3 | 230 | 3 /5 | 0 | 1 | 0 | -1/30 |
| x 4 | 240 | 4/5 | 0 | 0 | 1 | -1/10 |
| x 5 | 320 | 2/5 | 1 | 0 | 0 | 1/30 |
| f | 1280 | -7/5 | 0 | 0 | 0 | 2/15 |
| Базис | План | x 1 | x 2 | x 3 | x 4 | x 5 |
| x 3 | 50 | 0 | 0 | 1 | -3/4 | 1/24 |
| x 4 | 300 | 1 | 0 | 0 | 5/4 | -1/8 |
| x5 | 200 | 0 | 1 | 0 | -1/2 | 1/12 |
| f | 1700 | 0 | 0 | 0 | 7/4 | -1/24 |
| Базис | План | x1 | x2 | x3 | x4 | x5 |
| x3 | 1200 | 0 | 0 | 24 | -18 | 1 |
| x4 | 450 | 1 | 0 | 3 | -1 | 0 |
| x5 | 100 | 0 | 1 | -2 | 1 | 0 |
| f | 1750 | 0 | 0 | 1 | 1 | 0 |
В последнем плане строка f не содержит отрицательных значений, план x 1 = 450, x 2 = 100 оптимален, целевая функция принимает значение 1750.
Таким образом, чтобы получить максимальную прибыль, предприятию необходимо производить 450 полок вида А и 100 полок вида В, при этом прибыль составит 1750 ден. ед., а останется неиспользованными 1200 минут (20 часов) машинного времени.
Примеры заданий
Задача о застройке микрорайона
Для застройки микрорайона имеются n типовых проектов зданий, в каждом из которых предусмотрено m типов квартир. Стоимость одного здания каждого типа соответственно равна с1, с2, …, с n рублей; количество квартир i – ого типа в одном доме j – ого типа равно aij; потребность в квартирах j – ого типа – bi.
Необходимо составить план застройки микрорайона, удовлетворяющий потребности в квартирах, для которого затраты на строительство будут минимальны.
Исходные данные удобно записать в таблице:
| Типы домов Типы квартир | 1 | … | j | … | n | Потребности в квартирах |
| 1 | a11 | … | a1j | … | a1n | b1 |
| … | … | … | … | … | … | … |
| i | ai1 | … | aij | … | ain | bi |
| … | … | … | … | … | … | … |
| m | am1 | … | amj | … | amn | bm |
| Стоимость одного дома каждого типа | с 1 | … | с j | … | с n |
Обозначим через xj – число домов j – ого типа, тогда вектор x ={ x 1,…, xn } даст нам план застройки. Получаем следующую задачу линейного программирования: найти такие числа 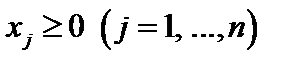 , которые удовлетворяют условиям:
, которые удовлетворяют условиям: 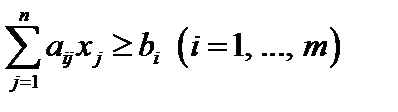 и для которых функция Z (затраты на строительство)
и для которых функция Z (затраты на строительство) 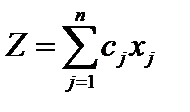 минимальные. Задача решается симплекс-методом.
минимальные. Задача решается симплекс-методом.
| Типы домов Типы квартир | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 0 | Потребности в квартирах |
| 1 | 10 | 15 | 20 | 0 | 30 | 25 | 15 | 0 | 12 | 14 | 100 |
| 2 | 20 | 14 | 15 | 10 | 0 | 25 | 15 | 14 | 12 | 20 | 200 |
| 3 | 30 | 15 | 12 | 10 | 15 | 20 | 0 | 14 | 17 | 20 | 150 |
| 4 | 0 | 12 | 13 | 15 | 30 | 12 | 10 | 15 | 20 | 0 | 140 |
| 5 | 13 | 14 | 15 | 20 | 30 | 0 | 13 | 15 | 20 | 25 | 250 |
| 6 | 12 | 15 | 20 | 25 | 15 | 14 | 13 | 20 | 30 | 0 | 183 |
| 7 | 13 | 12 | 25 | 13 | 16 | 17 | 15 | 20 | 0 | 15 | 231 |
| 8 | 0 | 14 | 15 | 20 | 13 | 25 | 14 | 17 | 20 | 0 | 145 |
| 9 | 15 | 20 | 16 | 30 | 20 | 16 | 15 | 25 | 15 | 0 | 156 |
| 10 | 17 | 15 | 14 | 25 | 15 | 13 | 20 | 27 | 16 | 0 | 210 |
| Стоимость одного дома каждого типа | 10 | 15 | 20 | 14 | 12 | 15 | 20 | 10 | 15 | 14 |
Задание
Дата добавления: 2019-01-14; просмотров: 356; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
