Метод потенциалов на примере решения задачи

Метод потенциалов предназначен для решения транспортной задачи в матричной постановке.

Таблица для метода потенциалов имеет следующий вид:

	B1 …	Bj	…Bn	u
A1 …	C11 x11	C1j x1j	C1n x1n	u1 …
Ai	Ci1 xi1	Cij xij	Cin xin	ui
… Am	Cm1 xm1	Cmj xmj	Cmn xmn	… um
v	v 1 …	vj	…vn	z

 

Каждая ячейка (i,j) таблицы хранит информацию о цене (C _ij) и о количестве перевозимого товара (x_ij). В процессе решения задачи часть клеток будем называть базисными (их всегда будет m+n−1), а остальные — небазисными (или свободными).

Алгоритм метода потенциалов

Шаг 0. Сделать задачу закрытой, если она открыта. Перейти на шаг 1.

Шаг 1. Нарисовать начальную таблицу. Перейти на шаг 2.

Шаг 2. Рассчитать начальный план (например, методом северо-западного угла) и выделить базисные клетки. Вычислить значение целевой функции. Перейти на шаг 3.

Шаг 3. Рассчитать значения потенциалов. Положить u₁=0 (или любому другому числу). Остальные потенциалы рассчитать с помощью базисных клеток, исходя из уравнения u_i+v_j=c_ij. Перейти на шаг 4.

Шаг 4. Для свободных клеток рассчитать оценки S _ij =c_ij−u_i−v_j. Если все S _ij >0, то найдено оптимальное решение. Перейти на шаг 6. Иначе выполнить шаг 5.

Шаг 5. Из небазисных клеток выбрать ту, у которой оценка s_ij минимальна и для нее выполнить следующую процедуру:

1) Построить цикл для этой клетки. Цикл — это замкнутая ломаная линия, которая чередует вертикальное и горизонтальное направления и проходит только по базисным клеткам. В исходной клетке поставить «+» и далее по циклу расставить, чередуя, «+» и «−». 

2) Вычислить λ = min{x_ij:«-»}. Клетку, на которой достигается этот минимум, убрать из базиса (только одну), а клетку (i,j) (у которой минимальная оценка s_ij) сделать базисной. 

3) Нарисовать новую таблицу, с пересчитанным планом перевозок: для клеток с «+» прибавить λ к x_ij а для клеток с «−» — вычесть. Остальные клетки остаются как были. Пересчитать целевую функцию.

Перейти на шаг 3.

Шаг 6. Конец алгоритма.

На шаге 3 у нас m+n−1 уравнение и n+m неизвестных. Поэтому возникает неоднозначность, разрешить которую можно, определив одну из переменных заранее (например, u₁=0).

Пример задачи

Рассмотрим задачу с тремя складами и двумя магазинами. Цены перевозок даны в таблице:

 

B A	10	10
10	10	5
5	5	10
10	5	10

 

Задача не замкнута, поэтому добавляем фиктивный магазин мощностью 5, стоимость перевозки в который равна нулю. После этого потребности магазинов и возможности складов равны. Окончательные цены перевозок приведены в таблице:

B A	10	10	5
10	10	5	0
5	5	10	0
10	5	10	0

 

Построим начальную таблицу и рассчитаем оценки методом северо-западного угла. Базисные клетки выделим серым цветом. Количество единиц товара, необходимого для перевозки из пункта производства в пункт потребления выделим зеленым цветом.

	10		10		5		U
10	10		5		0
		10
5	5		10		0
				5
10	5		10		0
				5		5
v

Рассчитаем потенциалы и значение целевой функции:

u₁=0; v₁=c₁₁-u₁=10-0=10;

u₂=c₂₁-v₁=5-10=-5

v₂=c₂₂-u₂=10-(-5)=15

u₃=c₃₂-v₂=10-15=-5

v ₃ = c ₃₃ - u ₃ =0-(-5)=5

Z=10*10+10*5+10*5+5*0=200

	10		10		5		u
10	10		5		0		0
		10
5	5		10		0		-5
				5
10	5		10		0		-5
				5		5
v	10		15		5		200

 

Оценки для свободных клеток равны:

s₁₂=5-0-15=−10;

s₁₃=0-5-0=−5;

s₂₁=5-(-5)-10=0

s ₂₃ =0-5-(-5)=0

s₃₁=0.

Среди оценок есть отрицательные, значит, решение не оптимально.

Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) - свободными. План называется вырожденным, если количество базисных клеток в нем меньше, чем m+n –1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся, поэтому клетка (2,1) становится базисной с объемом перевозки 0.

Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим! План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце.

Выберем клетку с минимальной оценкой, это (1,2), построим через неё цикл и расставим знаки:

	10		10		5		u
10	10	-	5	+	0		0
		10
5	5	+	10	-	0		-5
		0		5
10	5		10		0		-5
				5		5
v	10		15		5		200

 

Цикл здесь: (1,2) → (2,2) → (2,1) → (1,1) → (1,2). Минимальное из тех перевозок, где стоит знак «−», равно 5 (клетка (2,2), поэтому она покидает базис). Значение λ=5. Таким образом, новое значение целевой функции будет равно Z =10*5+5*5+5*5+10*5 = 150, а новый план перевозок записан в следующей таблице:

	10		10		5		u
10	10		5		0
		5		5
5	5		10		0
		5		0
10	5		10		0
				5		5
v							150

 

Повторяем процедуру заново, рассчитывая потенциалы и т. д.:

	10		10		5		u
10	10		5		0		0
		5		5
5	5		10		0		-5
		5		0
10	5		10		0		5
				5		5
v	10		5		-5		150

 

Потенциалы:

u₁=0;

v₁=10;

u₂=c₂₁-v₁=5-10=-5;

v₂=c₁₂-u₁=5-0=5;

u₃=c₃₂-v₂=10-5=5;

v₃=c₃₃-u₃=0-5=-5;

Оценки для свободных клеток:

s₁₃ = c₁₃-u₁-v₁=0-0-(-5)=5;

s₂₂ = c₂₂-u₂-v₂=10-5+5=10;

s₂₃ = c₂₃-u₂-v₃=0+5+5=10;

s ₃₁ = c ₃₁ - u ₃ - v ₁ =5-5-10=-10

Среди оценок есть отрицательные, поэтому решение не оптимально, строим цикл.

Цикл: (3,1) → (1,1) → (1,2) → (3,2) → (3,1).

	10		10		5		u
10	10	-	5	+	0		0
		5		5
5	5		10		0		-5
		5		0
10	5	+	10	-	0		5
				5		5
v	10		5		-5		150

 

Минимальной из тех перевозок, где стоит знак «−», нет, обе равны 5 (клетки (1,1) и (3,2) , поэтому можно выбрать любую клетку, которая покинет базис). Значение λ=5. Таким образом, новый план перевозок записан в следующей таблице, а значение целевой функции равно:

Z=5*10+5*5+5*5+5*0 +10*0 =100

	10		10		5		u
10	10		5		0		0
				10
5	5		10		0		5
		5		0
10	5		10		0		5
		5		0		5
v	0		5		-5		100

        

Повторяем вновь поиск потенциалов и оценок:

u₁=0;

v₂=c₁₂-u₀=5-0=5;

u₃=c₃₂-v₂=10-5=5;

v₁=c₃₁-u₃=5-5=0;

u₂=c₂₁-v₁=5-0=5;

v₃=c₃₃-u₃=0-5=-5;

s₁₁=10

s₁₃=5

s₂₂=0

s₂₃=0.

Все оценки неотрицательны, поэтому решение оптимально.

z=100, x₁₂=10, x₂₁=5, x₃₁=5, x₃₃=5.

Примеры заданий

Транспортная задача

Имеется m (i =1, …, m) пунктов отправления с запасами a_i (i =1, …, m) единиц однородного продукта, предназначенного к отправке. Этот продукт следует доставить в n (j =1, …, n) пунктов назначения с потребностями b_j (j =1, …, n) единиц того же продукта. Кроме того, задана матрица 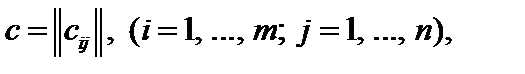 где c_ij – стоимость перевозки единицы продукта из i – ого пункта отправления в j –ый пункт назначения. Обозначим x_ij – количество перевозимого товара из i – ого пункта отправления в j –  ый пункт назначения.

Надо составить такой план перевозок 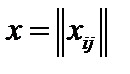, который удовлетворяет условиям

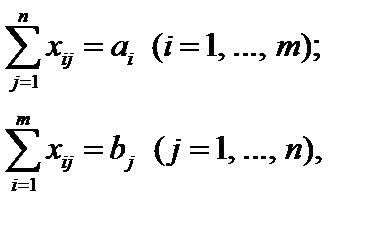
и для которого стоимость перевозок 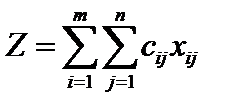 минимальна.

 

Пункты назнач.   Пункты отправлен.	1	2	3	4	5	6	7	8	9	1 0	Запасы
1	5	1	4	5	8	2	1	3	5	7	1 2 0
2	4	4	5	6	8	7	5	3	1	2	3 00
3	6	2	6	8	9	5	3	1	7	2	1 2 0
4	7	4	7	7	9	1	5	2	7	3	1 6 0
5	2	1	4	6	1	7	2	5	1	3	50
6	4	2	1	1	8	10	1	2	1	12	50
7	4	7	8	11	13	5	7	9	6	4	50
8	6	4	4	13	15	7	13	9	11	14	45
9	4	11	8	6	12	2	7	8	4	5	9 5
10	9	9	10	12	16	5	10	9	4	8	1 8 0
Спрос	10 0	10 0	10 0	2 0 0	2 0 0	35	75	75	10 5	10 0

 

Задание 1

№ вар.	№ строк таблицы	№ столбцов таблицы	№ вар.	№ строк таблицы	№ столбцов таблицы
1	1, 2, 3, 4	1, 2, 3, 4	14	6, 7, 8, 10	6, 7, 8, 9
2	2, 5, 6, 7	1, 2, 3, 7, 8	15	4, 5, 6, 7	1, 6, 7, 8
3	2, 5, 6, 7	3, 4, 7, 8	16	7, 8, 9, 10	7, 8, 9, 10
4	8, 9, 4, 2	4, 5, 2, 3	17	2, 4, 6, 8	2, 4, 6, 8
5	6, 7, 8, 9	8, 9, 7, 5, 6	18	1, 3, 5, 7	1, 3, 6
6	1, 3, 4	1, 2, 3, 10	19	4, 6, 8, 10	4, 6, 8, 10
7	4, 8, 5, 6, 7	7, 8, 9, 10	20	4, 5, 9, 10	3, 5, 9, 10
8	2, 4, 5, 6	1, 4, 9, 10	21	5, 8, 9, 10	5, 8, 9
9	1, 3, 6, 8	1, 3, 6, 7	22	2, 4, 9, 10	4, 5, 9, 10
10	5, 6, 8, 9	3, 6, 9	23	1, 5, 6, 9	6, 7, 8, 9
11	4, 5, 7, 8	2, 3, 9	24	2, 4, 8, 9	1, 2, 3, 4
12	3, 7, 8, 10	1, 2, 7, 10	25	4, 5, 6, 7, 10	5, 6, 7, 8
13	1, 4, 5, 6	1, 2, 7, 8	26

 

ЭЛЕМЕНТЫ ТЕОРИИ ИГР

---

Дата добавления: 2019-01-14; просмотров: 324; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!